基于猶豫模糊圖的信息識別與檢測?
陳 辰
(武漢數(shù)字工程研究所 武漢 430205)
1 引言
多屬性決策作為現(xiàn)代決策理論的重要分支,對模式識別與信息決策起到重要作用。在現(xiàn)實(shí)的決策環(huán)境中,決策者對信息的識別和處理存在著不完整性、不可分辨性、模糊性等,為了處理不精確與模糊信息,美國數(shù)學(xué)家、控制論專家Zadeh[1,9,16]提出了模糊邏輯和模糊集的概念,現(xiàn)已被廣泛應(yīng)用。然而,考慮到?jīng)Q策者認(rèn)知的差異性和思維的復(fù)雜性,對相同的信息做出的決策互不相同,且難以達(dá)成一致意見。為了應(yīng)對在決策時(shí)出現(xiàn)這種猶豫不決的狀況,西班牙學(xué)者Torra[2]于2009 年首次給出了猶豫模糊集的定義,該理論的提出可以更加地反映和兼顧每一個(gè)決策者的偏好程度,更加逼近真實(shí)的決策環(huán)境,為模糊信息的識別起到了重要的作用。近年來徐澤水[5,11~15]等對猶豫模糊集作了大量研究。
模糊圖的概念最早是由Rosenfeld[3]于1975 年提出,隨后Rosenfeld 給出了模糊圖之間的模糊關(guān)系,并且得出了模糊環(huán)境下圖的一些結(jié)論。超圖和模糊超圖的提出為解決復(fù)雜系統(tǒng)中的實(shí)際問題提供了分析方法,而且圖的許多應(yīng)用可以推廣到超圖。近年來許多學(xué)者對超圖的運(yùn)算圖做出了研究。2017 年,鞏增泰等[6,8,10]討論了模糊超圖的運(yùn)算圖,總結(jié)了超圖的計(jì)算的定義,研究了超圖的運(yùn)算圖的性質(zhì)。自猶豫模糊集問世以來,其相關(guān)理論和方法已經(jīng)成為決策科學(xué)的重要研究對象。張超和李德玉[4]利用猶豫模糊集的定義,于2017年首次給出了猶豫模糊圖的定義,并且通過模糊圖論的一些運(yùn)算性質(zhì)討論了兩個(gè)猶豫模糊圖的笛卡爾積,并和聯(lián)等運(yùn)算。2020年,鞏增泰和王俊虎[7]建立了猶豫模糊超圖的定義,并將其應(yīng)用到信息識別與多屬性決策之中。
2 預(yù)備知識

3 基于猶豫模糊超圖的信息檢測算法
對于模糊信息的識別在計(jì)算機(jī)工程中有著重要的作用,如何將某個(gè)方案或者計(jì)劃進(jìn)行選擇與檢測,是一個(gè)非常重要的環(huán)節(jié)。信息識別與檢測過程的描述如下。
針對某一信息識別下的猶豫模糊多屬性決策問題,將不同決策者對信息識別與檢測的結(jié)果統(tǒng)計(jì)整理,并對所得到的信息進(jìn)行分類融合,可對不同的方案作出不同的檢測與排序,進(jìn)而對各備選方案作出最佳選擇。
下面我們給出一個(gè)利用猶豫模糊超圖對信息識別與檢測的算法。
step 1 將決策者對不同方案的評判值進(jìn)行整合,得到一個(gè)關(guān)于評判值的猶豫模糊信息矩陣,并將矩陣中的數(shù)據(jù)進(jìn)行分類與整合。
step 2 將所得矩陣與猶豫模糊超圖相結(jié)合,并繪制出與之相符合的猶豫模糊超圖模型。
step 3 根據(jù)每個(gè)方案ui的評判信息,計(jì)算出每個(gè)方案中各屬性ai的得分函數(shù)。

step 4 將所有方案中的相同屬性整合到一起,構(gòu)成一個(gè)杻。用step 3 中得到的得分函數(shù)值給λi,用λi得到的超圖模型,得出檢測的屬性ai。
step 5 在得到的不同的屬性圖中,找出每個(gè)方案達(dá)到檢測的屬性個(gè)數(shù)并且排序,來完成對信息的識別與檢測,得到最佳方案。
4 實(shí)例分析
某企業(yè)董事會決定對接下來的五年進(jìn)行規(guī)劃,請3 位專家對4 個(gè)規(guī)劃方案u1,u2,u3,u4基于5 個(gè)不同屬性a1為商業(yè)前景,a2為財(cái)務(wù)支出,a3為顧客滿意度,a4為成長前景,a5為企業(yè)效益進(jìn)行評估。由于3位專家來自不同的領(lǐng)域,做出的評估信息也各不相同,也可能未作出評判其評判信息矩陣(見表1)。
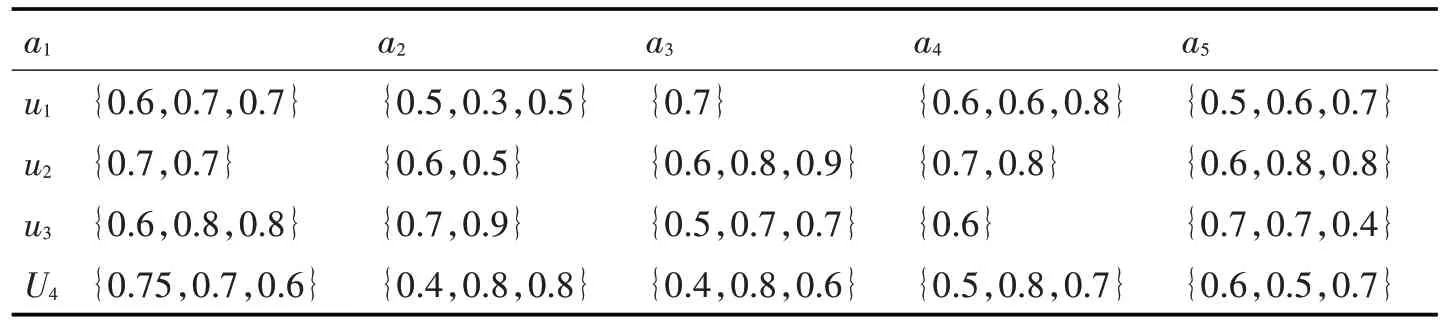
表1 猶豫模糊評判矩陣
step 1 關(guān)于決策者對方案的識別信息如表1。計(jì)算出每個(gè)方案中屬性的得分函數(shù)如下:
step 2 將評判信息矩陣與猶豫模糊超圖結(jié)合,得到關(guān)于屬性的猶豫模糊超圖模型。
step 3分別計(jì)算出每個(gè)屬性的得分函數(shù)。
step 4將得到的得分函數(shù)分別值給λ,則有
λ1=0.695,λ2=0.62,λ3=0.67,λ4=0.68,λ5=0.63。
通過對得出的猶豫模糊超圖模型進(jìn)行計(jì)算與分割,可知達(dá)到屬性a1意度的方案為u1,u2。達(dá)到屬性a2 意度的方案為u3,u4。達(dá)到屬性a3意度的方案為u1,u3。達(dá)到屬性a4 意度的方案為u1,u2,a4。達(dá)到屬性a5意度的方案為u2。
用每一個(gè)λi去得到的猶豫模糊超圖模型,可以得出不同的圖如下:
step 5每個(gè)方案達(dá)到檢測的屬性個(gè)數(shù)分別為:
方案u1有3個(gè),方案u2有2個(gè),方案u3有3個(gè),方案u4有2個(gè),對于方案u1和方案u3,

因?yàn)镾u2(ai)≥Su4(ai),則方案u2優(yōu)于u4
最終各個(gè)備選方案的排序?yàn)椋簎3>u1>u2>u4。
5 結(jié)語
本文在已有知識的基礎(chǔ)上,利用猶豫模糊超圖和粒計(jì)算,對模糊信息進(jìn)行檢測,得出了一個(gè)關(guān)于模糊信息識別及其最佳方案排序的算法,并利用算例說明了該算法的可行性。 與此同時(shí),針對屬性中帶有權(quán)重的相關(guān)內(nèi)容,用超圖解決將是我們今后的一個(gè)重要研究方向。

