Logistic混合模型的變分貝葉斯推斷

龔 斌,趙 凝,鄭 靜

(杭州電子科技大學(xué)經(jīng)濟學(xué)院,浙江 杭州 310018)

0 引 言

然而,單一的概率模型無法滿足實際的應(yīng)用需求,于是有學(xué)者Pearson K[4]首次提出概率混合模型的概念。概率混合模型可以使用多個獨立的概率分布去描述一個復(fù)雜的、使用單一概率模型無法描述,并且更符合現(xiàn)實中實際情況的數(shù)據(jù)分布。相比于單一的概率模型,混合模型具有諸多優(yōu)點,因此若是能夠?qū)我坏腖ogistic回歸模型推廣到Logistic混合模型,不僅能夠處理應(yīng)對更復(fù)雜的數(shù)據(jù)集,同時也能擴大模型在一些熱門領(lǐng)域的應(yīng)用。

變分貝葉斯方法(Variational Bayesian Inference)[5][6][7]作為目前最有效的確定性近似方法,由于其計算成本小、收斂速度快、可用于大規(guī)模數(shù)據(jù)集處理而備受關(guān)注,常被用于解決概率混合模型的參數(shù)估計問題。鄭丹陽等人[8]提出了一種基于變分推斷的聯(lián)合概率數(shù)據(jù)關(guān)聯(lián)算法,用于解決關(guān)于雷達鄰近多目標跟蹤的問題,結(jié)果表明新算法具備更高的位置精度,且能有效地避免因鄰近目標數(shù)量增多而引起的計算上的組合爆炸問題。劉連等人[9]針對傳統(tǒng)的字典學(xué)習(xí)算法收斂速率慢、受到噪聲干擾等問題提出一種基于變分推斷的字典學(xué)習(xí)算法,顯著提高了字典學(xué)習(xí)效率以及對測試圖像的去噪效果和重構(gòu)精度。

1 Logistic混合模型及其算法

1.1 Logistic混合模型

對于一組d維數(shù)據(jù)x=(x1,x2,…,xd)T,y∈{-1,1},假設(shè)w=(w1,…,wd)T為d維系數(shù),則Logistic回歸模型的密度函數(shù)p(y|x,w)可以表示為

p(y|x,w)=σ(ywTx)

(1)

接下來將其擴展至兩分量Logistic混合模型。假設(shè)有N組d維數(shù)據(jù),X={x1,x2,…,xN},xi∈Rd,i=1,2,…N,對應(yīng)的應(yīng)變量為Y={y1,y2,…,yN}。假設(shè)W={w1,w2}為系數(shù)參數(shù),π={π1,π2}為權(quán)重參數(shù),則兩分量Logistic混合模型的密度函數(shù)為

(2)

(3)

得到似然函數(shù)為

(4)

為方便起見,假設(shè)π={π1,π2}的先驗分布是參數(shù)為α=(α0,α0)T的Dirichlet分布[10],即

(5)

同時假設(shè)wk服從協(xié)方差矩陣相同,均值不同的正態(tài)分布,即

(6)

兩分量Logistic混合模型中各隨機變量的關(guān)系如圖一所示,其中隨機變量用圓表示,變量之間的關(guān)系用有向箭頭表示。綜上(2)-(6)式,根據(jù)貝葉斯規(guī)則,可以得到觀測值D和各個隨機變量Θ={Z,W,π}之間的聯(lián)合密度函數(shù)。

p(Z,W|D)∝p(Z,W,D)=p(Z,W,π,D)=p(D|Z,W)p(Z|π)p(π)p(W)

(7)

圖1 兩分量Logistic混合模型中各隨機變量的關(guān)系示意圖

1.2 變分貝葉斯推斷

通常在使用概率混合模型解決實際問題時,還需要解決參數(shù)估計和模型選擇這兩個方面的問題。本文通過將模型分量數(shù)固定為兩分量來解決模型選擇的問題,后續(xù)將問題聚焦于如何解決兩分量Logistic混合模型的參數(shù)估計上。而常用的混合模型往往會因為模型結(jié)構(gòu)過于復(fù)雜而難以求解目標后驗分布,因此通常使用變分貝葉斯推斷方法來近似后驗分布。

變分貝葉斯的主要思想是選擇一族容易處理的分布族q(Θ)來近似真實的后驗分布p(Θ|D)。首先假設(shè)變分分布族滿足平均場理論,即

q(Θ)=q(Z,W,π)=q(Z)q(W)q(π)

(8)

又由貝葉斯定理得到

(9)

(10)

σ(z)≤exp[ξ*z-H(ξ)]

(11)

其中H(ξ)=-ξ*ln(ξ)-(1-ξ)*ln(1-ξ)

通過(11)將(10)中包含Logistic函數(shù)的部分轉(zhuǎn)化為近似表示,即

(12)

(13)

1.2.1 q(Z)的變分推斷

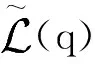
(14)

(15)

其中

(16)

且對于離散分布q(Z)而言,可以得到E(Z)(Znk)=rnk。

1.2.2q(π)的變分推斷

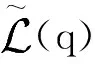
(17)

因此

(18)

其中αN=(αN1,αN2)T

(19)

1.2.3 q(W)的變分推斷

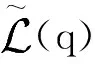
(20)

可得

其中Σk=I

(21)

進一步可得

(22)

根據(jù)上述推導(dǎo)得到的3個變分參數(shù)分布,進一步可得其中參數(shù)的期望:

E(W)(wk)=vk

(23)

E(π)(lnπk)=ψ(αNk)-ψ(αN1+αN2)

(24)

E(Z)(Znk)=rnk

(25)

其中ψ(·)為digamma函數(shù)。

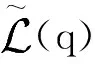
(26)

其中

(27)

(28)

(29)

(30)

(31)

(32)

整理得到

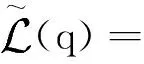
(33)

1.2.5 參數(shù)ξn的估計

通過將推導(dǎo)得到的(33)關(guān)于參數(shù)ξn求一階導(dǎo)并令為0,得到ξn的參數(shù)估計,即

(34)

可得

(35)

由于

(36)

(37)

對等式(37)兩邊同時關(guān)于ξn求導(dǎo)得到r′nk:

(38)

其中

其中ψ′(·)為digamma函數(shù)的一階導(dǎo)。

同樣對等式(36)兩邊同時關(guān)于ξn求導(dǎo)得到ρ′nk:

(39)

綜上根據(jù)(35)、(38)、(39),就得到了參數(shù)ξn的估計表達式:

(40)

其中

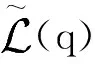
2 實證分析

為了驗證本文提出的兩分量Logistic混合模型變分貝葉斯算法的性能,通過將收集到的以下兩組數(shù)據(jù)集按不同比例的混合來進行擬合檢驗。其中數(shù)據(jù)集1為Iris(鳶尾花)數(shù)據(jù)集,該數(shù)據(jù)集中每個樣本有四個屬性和一個類別標簽,一共3個類別,為了更好地滿足對上述模型算法的檢驗,選擇其中兩類作為第一組二分類數(shù)據(jù)集;數(shù)據(jù)集2為Banknote(紙幣驗證)數(shù)據(jù)集,該數(shù)據(jù)集也是一組每個樣本擁有四個屬性以及一個類別標簽的二分類數(shù)據(jù)集。

實驗中,將超參數(shù)進行如下初始化:α0初始化為1,μk為樣本均值,wk用numpy庫中的random函數(shù)進行隨機初始化,權(quán)重系數(shù)πk都初始化為0.5。接下來將以上兩組數(shù)據(jù)集按三種不同比例的混合,分別運用本文提出的變分貝葉斯算法來進行模擬驗證。其中數(shù)據(jù)集A的混合比例為0.5,0.5;數(shù)據(jù)集B的混合比例為0.7,0.3;數(shù)據(jù)集C的混合比例為0.4,0.6。它們各自的變分下界變化趨勢如下圖所示。

圖2 數(shù)據(jù)集A的變分下界趨勢圖

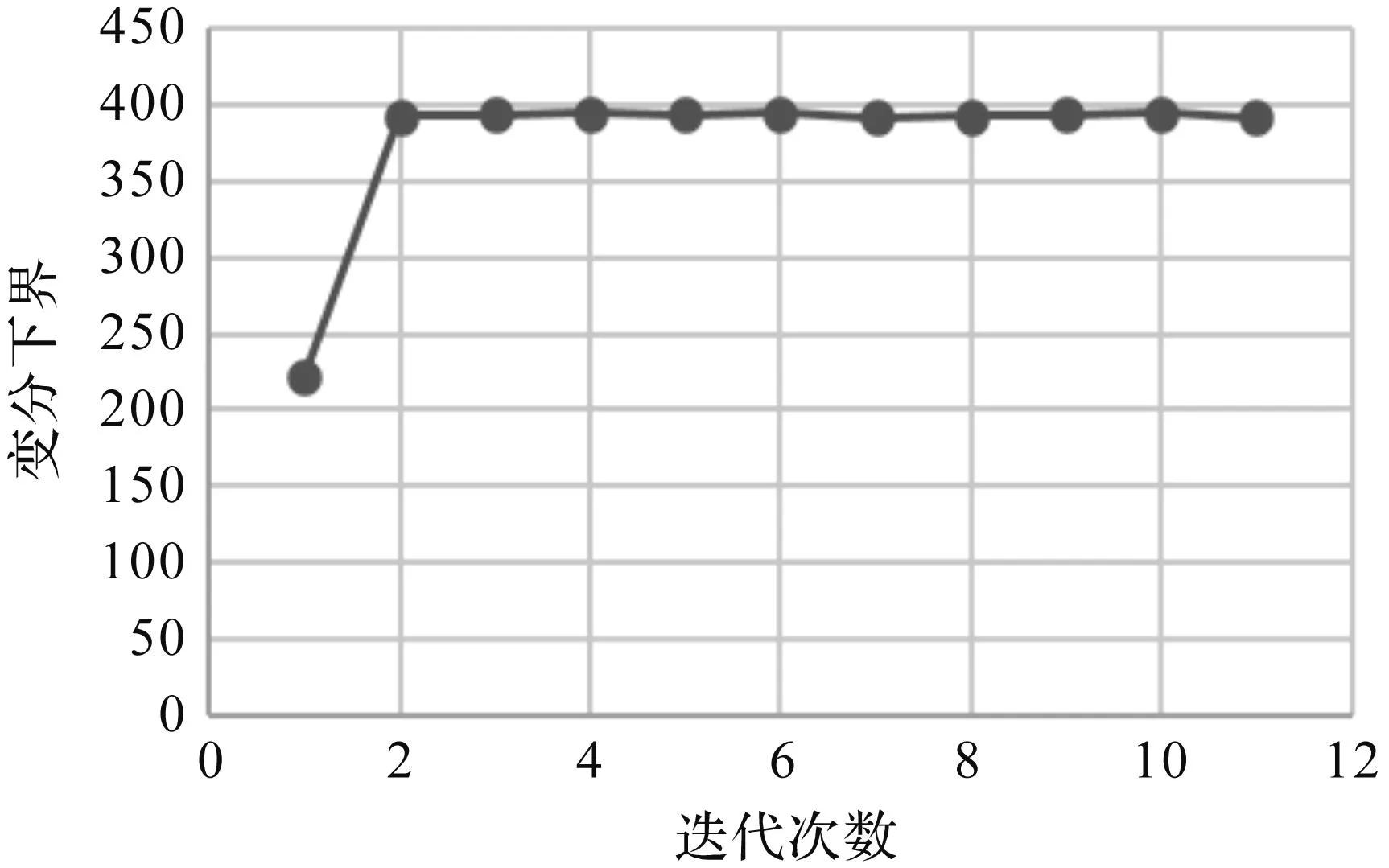
圖3 數(shù)據(jù)集B的變分下界趨勢圖

圖4 數(shù)據(jù)集C的變分下界趨勢圖

從上述趨勢圖中可以發(fā)現(xiàn),隨著迭代次數(shù)的增加,變分下界很快就開始收斂,之后逐漸趨于平穩(wěn)。

將變分下界進入收斂后的各個超參數(shù)以及參數(shù)的估計值結(jié)果整理如下表:

表1 三組混合數(shù)據(jù)集模型擬合結(jié)果

從表一的擬合結(jié)果來看,該算法在變分下界收斂達到平穩(wěn)后得到的權(quán)重系數(shù)估計值跟實際的混合比例非常接近,說明該模型算法能在快速收斂的同時實現(xiàn)較為精確的混合分類數(shù)據(jù)集的混合比例估計。

3 結(jié)束語

傳統(tǒng)的變分貝葉斯推斷在處理混合模型的參數(shù)估計時,通常需要依賴平均場理論以及分布之間的共軛關(guān)系,對于無共軛分布的混合模型便無法進行有效的參數(shù)估計。本文通過將Logistic混合模型與變分貝葉斯推斷法結(jié)合在一起,并借助Logistic函數(shù)的近似表示來解決不構(gòu)成共軛分布的問題,提出一種能用于解決Logistic混合模型參數(shù)估計的貝葉斯推斷算法,并給出了詳細的變分推導(dǎo)過程。實證結(jié)果表明,該算法能夠在保證精確估計混合比例的同時,實現(xiàn)快速收斂的效果。后續(xù)將針對如何實現(xiàn)拓展至多分類混合模型的變分貝葉斯推斷進行深入研究。