多策略融合的改進獅群算法及其工程優化
黃志鋒,劉媛華,張 聰
(上海理工大學 管理學院,上海 200093)
0 引 言
目前,算法可以分為經典啟發式算法和新型智能優化算法.經典啟發式算法有粒子群算法(PSO)、模擬退火算法(SA)和蟻群算法(ACO)等,雖然經典算法應用范圍廣,但由于建模簡單,求解精度不高.因此,近年來,許多學者針對算法進行改進和重新設計,提出了許多新型智能優化算法,如灰狼算法(GWO)[1]、鯨魚優化算法(WOA)[2]和獅群算法(LSO)[3]等,雖然新型智能優化算法較經典算法在求解精度上有所提高,但還存在些許缺點,如搜索能力不足、后期搜索效率低下等缺點.
獅群優化(Lion Swarm Optimization,LSO)算法是近年提出的一種新型智能優化算法.目前,LSO算法已經成功應用于二維路徑規劃、汽輪機熱耗功率模型預測、極限學習機廢水處理、水電站優化調度和二氧化碳排放預測等領域中.針對獅群算法存在的問題,學者們提出了許多改進策略來提高LSO算法的性能.黃志鋒[4]使用雙種群結構,重新構造獅群算法,提高算法尋優性能,使其能夠在二維路徑規劃當中具有較好的表現.汪嬋嬋[5]將禁忌搜索算法和獅群算法相結合,并加入非線性擾動因子和黃金正弦策略,提高算法的尋優能力.Yang等人[6]針對預測問題,首先將混沌理論融入獅群算法,將改進獅群算法對神經網絡參數進行優化,實驗表明,改進后算法搜索性能有所提高.Wu等人[7]針對獅群算法后期收斂速度緩慢、尋優能力不足等問題,提出了自適應參數和混沌搜索融入到算法中.Qiao等[8]針對獅群算法多樣性不足的問題,提出將遺傳算法與獅群算法融合,提高了算法的多樣性和隨機性,但融合遺傳算法增加了算法運行時間.李彥蒼等[9]針對獅群算法在不同解空間當中,幼獅步長擾動因子影響變化大,且后期收斂速度不足,提出了引入信息熵值實現算法自適應調節并增大算法的魯棒性.雖然以上改進提高了算法的性能,但改進后的算法很難在加快算法收斂度和避免陷入局部最優方面取得平衡,且改進后在測試函數方面提升不夠顯著.因此,本文提出一種使用混沌種群初始化、融合柯西變異、改進獅群步長和融合精英反向學習的多策略融合的改進獅群算法,以下稱MFLSO.
在標準LSO算法中,獅王負責全局最優個體的引導,即獅王位置為全局最優,且獅王只在最優值附近搜索,這樣導致算法側重局部搜索能力,全局尋優能力不足,易陷入局部極值.另外,獅群算法在計算高緯度問題時,跳出局部最優的能力不足.針對以上的不足,首先采用Tent映射,進行混沌種群初始化操作,使算法能夠歷遍解空間并提升初始解的質量;其次,融合柯西變異,修改獅群最優解的更新方程,對獅群最優位置進行擾動變異操作,提高擺脫局部極值的能力;再次,改進母獅更新方式和獅群步長公式,提高算法后期的搜索能力和尋優精度.最后,引入精英反向學習,避免算法早熟,提升算法收斂精度.
1 獅群優化算法
在LSO算法中,每只獅子的位置代表所求問題的潛在解決方案(答案),獵物的質量相對應于解決方案的質量即適應度值.現假設所求問題f(x)的空間維度為D,設置種群的數量為N,獅群可以用矩陣表示:
(1)
獅群的每一個獅子可以用一個D維向量表示:
Xi=(Xi1,Xi2,…,XiD),1≤i≤N
(2)
種群初始化:
xi,j=xmin,j+rand(0,1)·(xmax,j-xmin,j)
(3)
式中i=1,2,…,n;j=1,2,…,D;rand(0,1)是隨機數;xmin,j和xmax,j是第j維度的下限和上限.
獅群中成年獅的數量會影響最終優化結果.成年獅負責尋優,而幼獅的位置更新使算法更具有多樣性,有利于增強算法的差異性,使算法具有更強的搜索能力.成年獅比例因子β∈(0,1),因此為了平衡算法的收斂速度和尋優能力,設置β=0.3.
首先,為保證獅王能優先于其他獅子進食獵物,獅王會在最佳位置周圍內進行搜索和小范圍移動,即適應度值最小的位置,獅王的更新公式為:
(4)
式(4)中xk+1代表獅王每次迭代后獅群中的最優個體,gbestk為第k次迭代后獅群的最優解,Pbestk代表經歷k次循環后,獅王歷史最優位置,γ是[0,1]區間內服從高斯分布的一個隨機數.
其次,母獅群體主要負責識別并包圍獵物,狩獵時會選擇另一只母獅進行合作.母獅位置更新公式為:
(5)
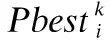
(6)
其中:
(7)

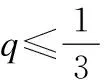
(8)

(9)
幼獅的移動需要在規定范圍內,ac為隨迭代次數遞減的線性擾動因子,隨著算法計算次數增加,步長隨之縮小,從而幫助幼獅先在更廣的范圍內搜索獵物,然后演變為獵物相鄰域的局部搜索:
(10)
2 改進獅群算法
2.1 基于混沌的種群初始化方法
對于采用并行迭代方式尋優的智能優化算法,種群初始化能決定算法求解的好壞,標準的LSO算法初始化采用式(3)rand函數隨機初始化個體,這種生成方式具有較大的隨機性,不會覆蓋整個解的空間區域,會降低算法的尋優效率.因此本文采用Tent混沌初始化種群的方法,混沌初始化能夠提高算法搜索的隨機性并充分分布解空間.
Tent混沌種群初始化操作如下:
(11)
當φ∈(0,1)且x∈[0,1]時,系統(11)處于混沌狀態.
2.2 融合柯西變異
在標準的LSO算法中,獅王只會在自身的附近進行小范圍的搜索,在算法的前中后期都可能陷入局部最優解.因此本研究為增強LSO算法跳出局部最優解的能力,采用柯西變異擾動對最優解進行變異,確保算法在局部尋優時具有更大的種群多樣性,加快種群逼近最優位置的速度.柯西變異是由柯西分布產生的,柯西分布概率密度如式(12)所示:
(12)
當a=1時,稱為標準柯西分布.從圖1可以看到,柯西分布,在0處的峰值為0.3,小于高斯;此外柯西分布更為平緩,下降的速度更為緩慢,柯西分布更加均勻,因此柯西相比高斯具有更強的變異擾動能力,更易擺脫局部最優,較小的峰值指導個體快速搜尋最優位置,所以本文將柯西變異引入到獅群算法每代最優個體中,發揮柯西變異算子的擾動能力,提升算法全局尋優性能.
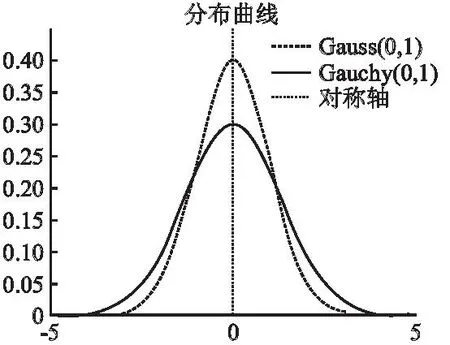
圖1 標準柯西、高斯分布概率密度曲線Fig.1 Probability density curve of standard Cauchy and Gaussian distribution
因此,獅群最優位置公式為:
Gbest(k)=gbestk+cauchy(0,1)⊕gbestk
(13)
其中,Gbest(k)表示第k代經柯西擾動后獅群的最優位置;gbestk表示第k代最優位置.柯西變異算子在獅群最優解位置即獅王位置進行擾動變異操作,加強算法跳出最優解的能力.
2.3 改進獅群步長公式和母獅行為
LSO算法中,幼獅和母獅位置的更新能決定算法尋優的質量,但如果優化問題的維度很大,即獅群的搜索空間很大,會使算法的步長step、參數αf和αc比較大,即隨著迭代次數增加,參數減小,但優化問題很大時,參數變化就不明顯,這會使得在算法的后期,母獅還在大范圍的搜索解,更像隨機搜索,算法的效率降低.因此,需要修改獅群的步長公式,使之能夠更好適應不同維度的問題.
(14)
改進后的步長和參數會隨著迭代次數的變化更加敏感,在大維度問題優化過程中,隨著迭代次數增加,算法后期能進行更精確的搜索,提高搜索效率.
為提高尋優能力,對母獅位置移動公式進行修改:
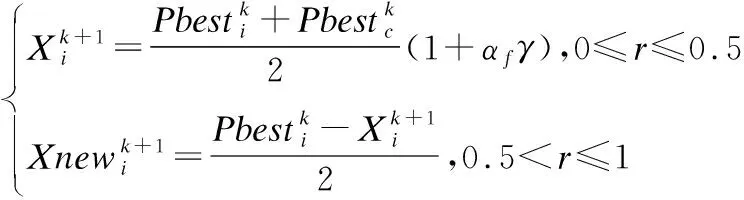
(15)
式中r∈[0,1]區間內隨機分布的一個數,當0≤r≤0.5時執行原來的更新方式;當0.5 Tizhoosh等人[10]于2015年提出反向學習機制,根據學者研究發現,反向解可以有效增加種群的多樣性和質量.郭雨鑫等人[11]提出融合反向學習的HHO算法,實驗顯示反向學習提升了算法的收斂性能和尋優能力.Saunhita[12]等人利用反向學習優化蛾焰算法,改善了其趨同性.反向學習的原理是根據當前解計算方向位置的解,接著從當前解和方向解的種群中選擇最優解作為下一代個體. 設在D維搜索空間中,獅群的可行解為: Xi=(xi,1,xi,2…,xi,D),(xj∈[xmin,j,xmax,j]) (16) xmin,j和xmax,j是第j維度的最小值(下限)和最大值(上限),其反向解為: (17) 其中: (18) 其中r是區間[0,1]上的隨機數字. 為避免反向解比當前解更難搜索到最優值,本文采用精英反向學習,能夠提高算法多樣性,避免早熟. 設獅群的可行解的極值點作為種群的精英個體: (19) 其反向解: (20) 其中: (21) (22) 綜上所述,本文提出的融合多策略獅群算法(記作MFLSO)的算法如下所示: 算法.MFLSO 1.Randomly generate ofNlion individuals using chaotic initialization. 2.while t 3.Calculate the number of lion king and lionesses in the lion swarm 4.Generate the opposite solution 5.Calculate Individual Search Boundary According to Upper and Lower Bounds 7. fori=1∶Number of adult lions 8. Update the location of the i-th lioness based on Eq.(14) 9. end for 10. fori=1∶Number of cubs 11. q=rand(0,1); 12. if q<1/3 13. The cub moves to the lion king and eats near the lion king 14. else if 1/3 15. The cub moves around the lioness and learns to hunt 16. else 17. The cub is driven away from the lion king 18. end if 19. end for 20. Update the location of the lion king according to Eq.(13) 21. fori=1∶Number of adult lions 22. The lion and the lioness mate to create a new cub 23. end for 24. Calculate the fitness value all updated lion positions 25.According to fitness,the firstnlions are retained and the rest were eliminated 26. t=t+1 27.end while 下面將對標準的LSO算法和本文的MFLSO算法進行復雜度分析比對. 假設獅群的規模為N,優化問題的維度為D,最大迭代次數為T,種群初始化的時間為t0,每一維隨機數的生成時間維t1,求解適應度值得時間維f(D),則標準的LSO初始化過程得時間復雜度用下式表示: T1=O(t0+N(f(D)+t1D))=O(f(D)+D) (23) 對獅群進行分類,獅王占據最優位置、母獅合作捕獵、幼獅跟隨學習的時間復雜度為O(N),計算個體適應度得時間復雜度為O(N*f(D)),所以LSO總的時間復雜度為: TLSO=O(f(D)+D)+O(N*f(D)) (24) 故LSO算法最終得復雜度為O(N),只有最高次數的N才有意義. 在獅王更新階段,采用式(13)進行柯西變異擾動策略產生最優解的時間為t1,母獅更新階段只是改變更新公式,時間復雜度并未改變,反向解的時間復雜度為O(N),綜上分析MFLSO時間復雜度為: TCLSO=O((f(D)+D)+O(N*f(D))+t1)+O(N)=O(f(D)+D) (25) 因此,MFLSO算法和LSO算法的復雜度相同,對算法的改進并沒有增加計算的負擔. 實驗環境:操作系統Windows 11(64bit),處理器AMD R7 5800H with Radeon Graphics.3.20 GHz,電腦內存16G,仿真平臺Matlab 2021a. 為了測試MFLSO算法處理函數優化問題的能力,本節將選取13個國際標準測試函數,如表1所示,其中F1~F6為多維單峰測試函數,F7~F9為多維多峰測試函數,F10~F13為固定維數多峰測試函數. 表1 國際標準測試函數Table 1 International standard test functio 選取8種算法作為對照組算法:GA、PSO、GWO、WOA、LSO、DCSOA-S[13](2021)、IHHO[14](2021)和ILSO[5](2021)以全面評估本文所提MFLSO算法的性能.其中GA交叉概率pc=0.8,變異概率pm=0.1;PSO學習因子c1=2,c2=2,慣性權重ω=0.8;GWO系數A=2;WOA狩獵行為概率ps=0.6,螺旋形態常數b=1;LSO和MFLSO成年獅比例β=0.3,其他算法參數見參考文獻. 為避免偶然性,所有算法參數設置一致,迭代次數tmax=500,維度D=30,種群規模均取N=30,每種算法獨立運行10輪,取每輪結果的平均值. 表2為測試結果,對于單峰測試函數F1~F4,本文所提算法能找到最優值并且算法在10輪運行中,均值和標準差最小,說明改進后的算法更具有穩定性和更好的收斂精度.在F5~F6沒有搜索到最優值,但是對比算法也沒有搜索到最優值,但相比于其他算法,本文算法收斂精度更高. 表2 測試函數結果對比Table 2 Comparison of test function results 多峰測試函數F7~F9的結果顯示,本文所提MFLSO算法相較于對比算法平均值和標準差最小,說明MFLSO算法在處理更復雜的問題時有更強的穩定性.雖然在函數F8上沒有找到最優值,但在幾個對比算法中,MFLSO尋優結果相比對比算法最接近理論最優值,表明算法具有較強的搜索能力.對于固維函數F10~F13,由于維數降低,9種算法求解的準確率均有所提高,運算簡單函數方面,算法的性能相差不大. 通過13個國際標準測試函數的實驗結果表明,本文所提的MFLSO算法,相比LSO算法有較大的提升.相較于對比算法,大部分測試函數尋優過程中,MFLSO算法平均值和標準差最小,穩定性最高、結果最接近理論最優值.總體而言,MFLSO算法在測試函數尋優中具有明顯優勢.部分函數收斂圖如圖2所示. 圖2 6種對比算法在部分測試函數上的收斂曲線Fig.2 Convergence curves of 6 comparison algorithm on some functions 為了更好地驗證MFLSO算法尋優的能力和魯棒性,本文選取CEC2014(國際進化計算大會)復雜函數中的部分單峰函數(UN)、多峰函數(MN)、混合型函數(HF),見表3.該測試函數相比標準測試函數更加復雜.設置種群數量為N=30,維度D=30,迭代次數tmax=1000,獨立運算10輪,計算平均值和標準差.將本文算法與GA、PSO、GWO、WOA、LSO五個算法進行對比. 由表4可知,MFLSO在單峰、多峰和混合類型的CEC測試函數尋優上表現最佳,相較于另外5種算法,MFLSO的結果最接近理論最佳值,標準差大多數情況下小于對比函數,說明MFLSO算法具有較好的尋優能力和穩定性. 表4 CEC2014函數測試結果(部分)Table 4 CEC2014 function test results(part) 結合3.1節的國際標準測試函數的結果和CEC2014測試函數的結果可以看出,LSO算法在一些國際標準測試函數表現不錯,但在CEC測試函數表現較差,LSO算法可能存在零點搜索偏好陷阱[13],即當測試函數的最優值為0時,LSO算法能快速收斂到最優值,但是當測試函數最優值不為0時,如CEC2014測試函數的最優值均不為0,LSO算法表現最差.MFLSO擺脫了零點搜索偏好陷阱,在國際標準測試函數和CEC2014測試函數的尋優表現較好,進一步驗證了改進算法的尋優能力. 總體而言,MFLSO在較為復雜的CEC2014函數上,也具有很好的穩定性和尋優能力. 壓力容器結構設計如圖3所示,目的是使各項成本總和最小.其中包括4個決策變量和4個約束條件,決策變量是外殼的厚度Ts(x1)、封蓋厚度Th(x2)、殼體半徑R(x3)以及圓柱形截面長度Ls(x4),其模型表示為: 圖3 壓力容器設計圖Fig.3 Structure design drawing of welded beam (26) 分別使用GA、PSO、GWO、WOA、LSO和MFLSO對該問題進行求解,并將6種算法的求解結果進行比較. 彈簧設計結構如圖4所示,使其在外力、震動頻率等約束條件下質量最小化,共有3個決策變量和4個約束條件,其中決策變量分別是直徑d(x1)、平均線圈直接D(x2)、繞線圈數N(x3),其數學模型如下: 圖4 彈簧結構設計圖Fig.4 Structure design drawing of tension spring (27) 實驗結果如表5和表6,從結果可以看出,MFLSO算法對拉壓壓力容器設計和彈簧設計優化問題效果要優于其他5種算法.通過對兩種工程實例測試,進一步驗證了MFLSO算法在實際工程領域具有可行性和一定應用前景,且效果較其他算法較好. 表5 7種不同算法求解壓力容器設計問題的最優解對比Table 5 Comparsion of optimal solution for the pressure vessel design problem by seven different algorithm 表6 7種不同算法求解壓力容器設計問題的最優解對比Table 6 Comparsion of optimal solution for the pressure vessel design problem by seven different algorithm 針對基礎LSO算法搜索效率低、易陷入局部極值和后期收斂性不足等問題,提出了一種改進獅群算法.首先,使用混沌生成初始種群,提高算法初始解的質量,使之能夠平均分布在整個解空間;其次,在算法最優解處引入柯西變異,提高算法逃出局部極值的能力;再次,改進母獅位置更新方式和獅群步長方程,提高算法后期的收斂精度和速度;最后,融合了精英反向學習,避免算法早熟,提高算法解的質量. 為了驗證改進算法的有效性,選取了13個國際通用測試函數和部分CEC2014測試函數進行仿真實驗,結果表明MFLSO算法性能最優,且具有較好的收斂精度;將MFLSO算法應用在工程實例中,所得結果最優.通過實驗證明本文所提MFLSO算法在測試函數尋優上和工程實際應用中相比其他算法具有明顯優勢.當然本算法也存在局限性,雖然在測試函數中所提算法收斂精度最高,但個別函數只能接近理論最優值,本算法還有進一步提高的空間.2.4 融合精英反向學習
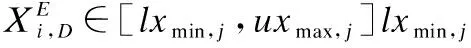
2.5 MFLSO算法步驟
2.6 MFLSO算法復雜度分析

3 實驗仿真及結果分析
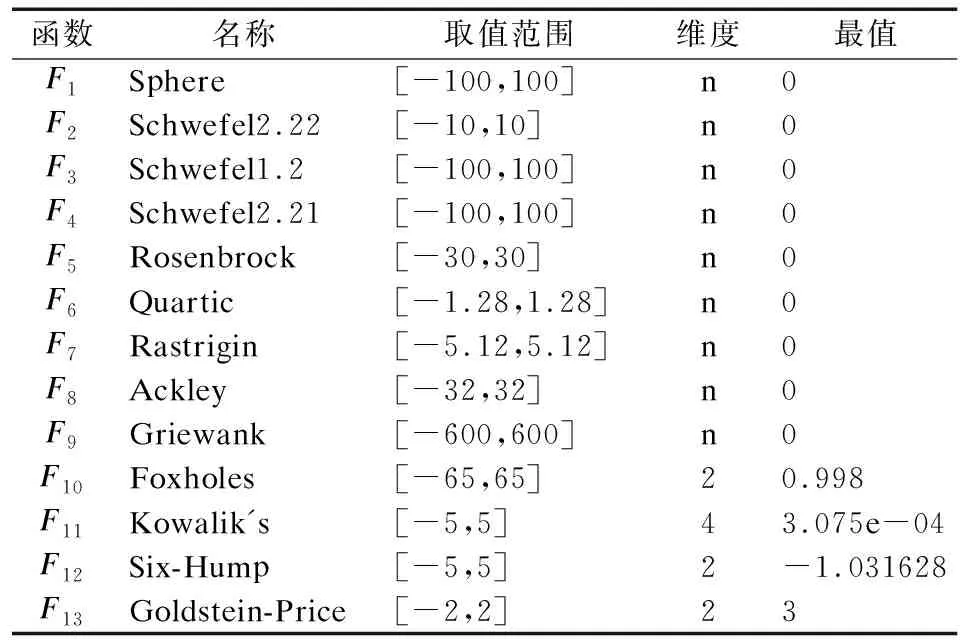
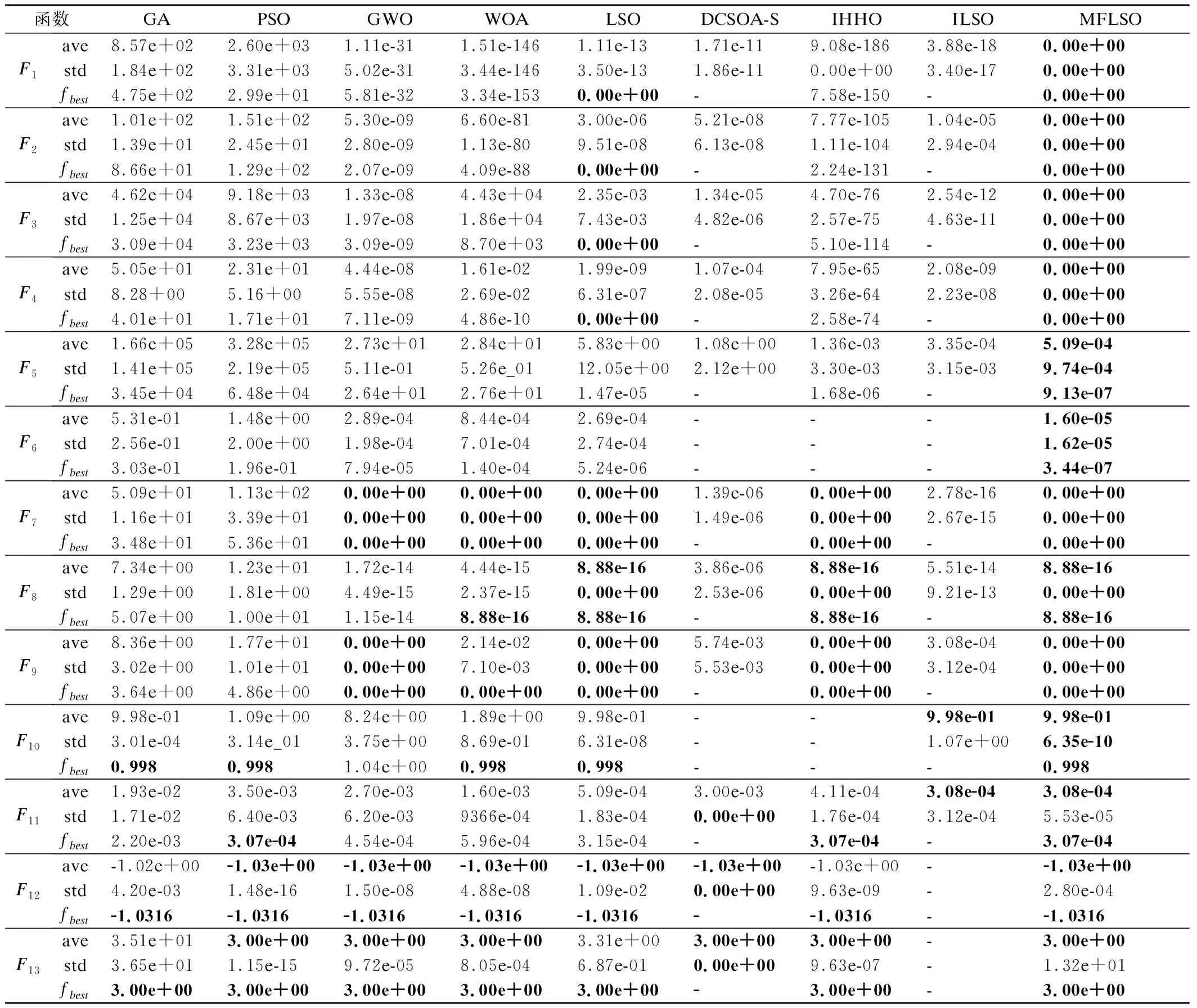
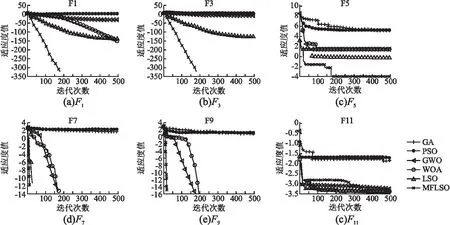
3.1 求解標準測試函數實驗
3.2 CEC2014復雜函數分析
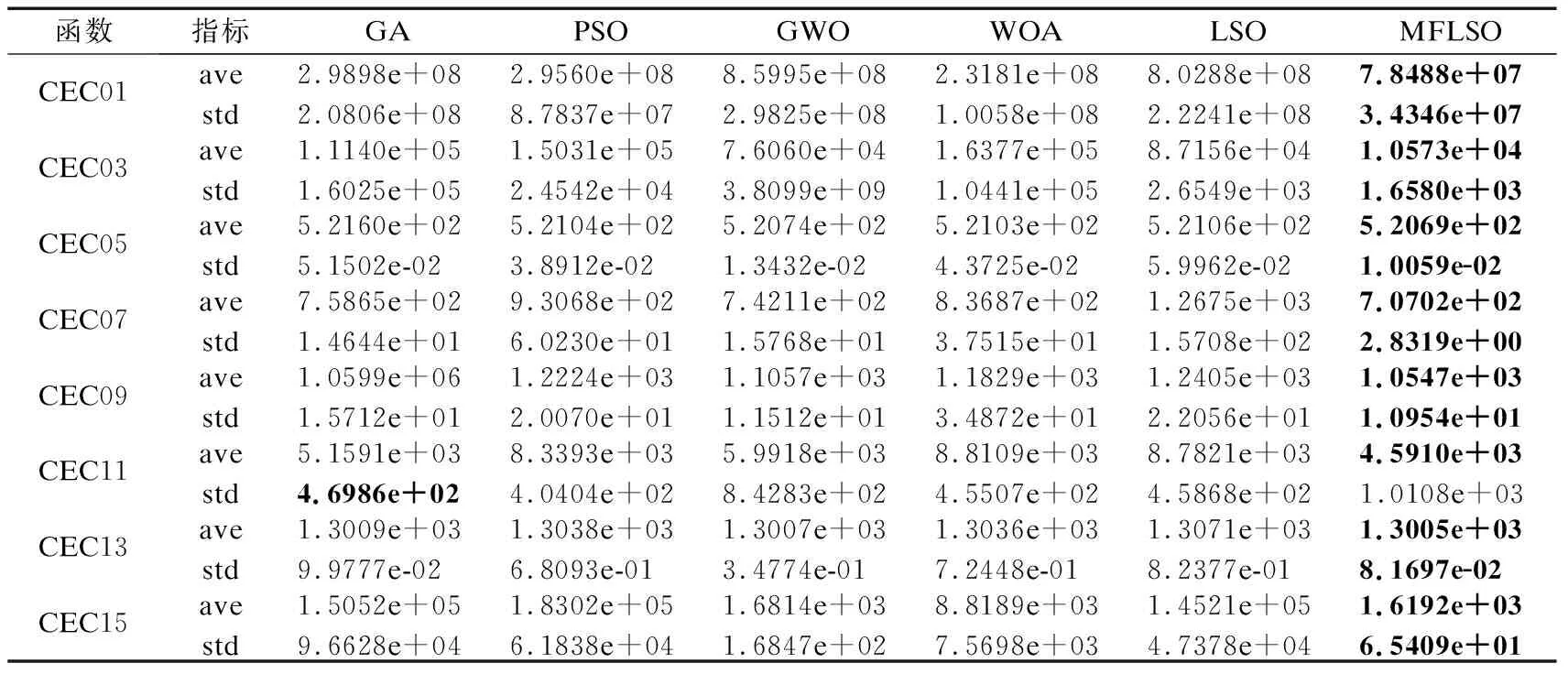
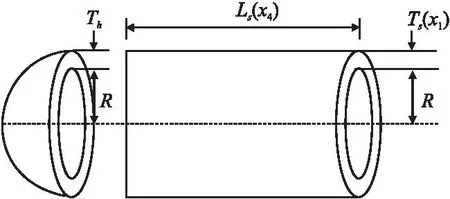
3.3 壓力容器設計問題
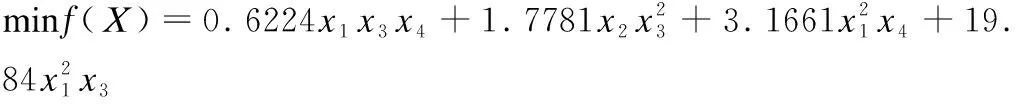
3.4 壓拉彈簧設計問題

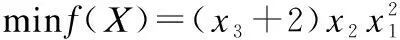
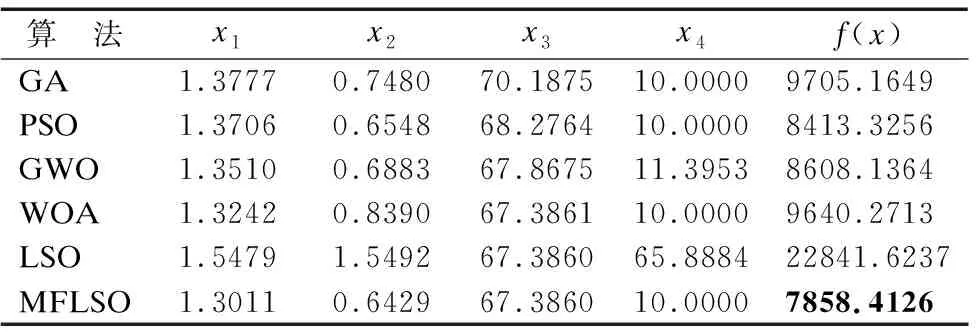
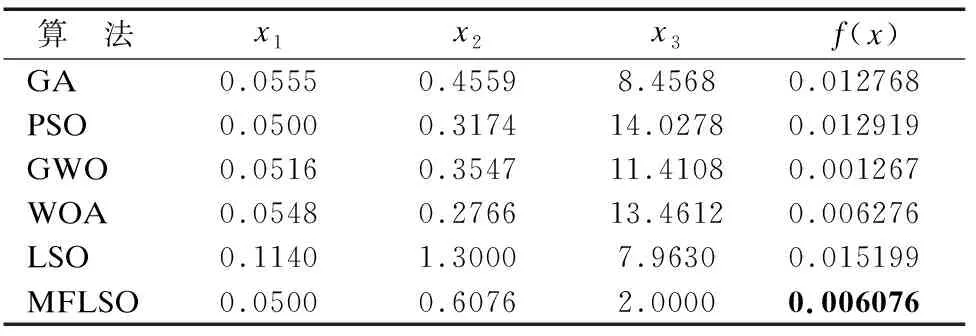
4 結 論

