一種改進(jìn)蟻群算法的路徑規(guī)劃研究

劉海鵬,念紫帥

(昆明理工大學(xué) 信息工程與自動(dòng)化學(xué)院,昆明 650500)

0 引 言

路徑規(guī)劃是機(jī)器人研究領(lǐng)域的一個(gè)關(guān)鍵問題.通常,路徑規(guī)劃是指機(jī)器人根據(jù)已知條件獨(dú)立規(guī)劃的安全無碰撞的路徑[1].路徑規(guī)劃使用的算法有遺傳算法[2]、人工勢(shì)場(chǎng)法[3]、粒子群算法[4]、A*算法[5]、RRT算法[6]等.然而,這些算法存在著穩(wěn)定性差、效率低等問題.與上述算法相比,蟻群算法具有魯棒性強(qiáng)、路徑規(guī)劃效果好等優(yōu)點(diǎn).但是,在復(fù)雜環(huán)境下,蟻群算法存在局部最優(yōu)、搜索時(shí)間長(zhǎng)等問題.

為此,許多專家學(xué)者從信息素更新以及與其他智能算法的結(jié)合等方面改進(jìn)了蟻群算法[7].文獻(xiàn)[8]通過設(shè)計(jì)一種基于路徑幾何特征的局部?jī)?yōu)化方法,進(jìn)一步優(yōu)化了初始路徑,顯著的提高了算法的收斂速度.文獻(xiàn)[9]通過引入懲罰因子,對(duì)死鎖路徑點(diǎn)上的信息素進(jìn)行懲罰,有效的減少了死亡螞蟻的數(shù)量,確保了解的多樣性.文獻(xiàn)[10]通過對(duì)路徑進(jìn)行幾何局部?jī)?yōu)化,并沿著勢(shì)場(chǎng)力的方向擴(kuò)散信息素,減小了螞蟻的搜索空間.文獻(xiàn)[11]采用進(jìn)化的思想改進(jìn)信息素更新策略,使算法的收斂速度得到提高.文獻(xiàn)[12]提出了一種孤狼-蟻群組合策略.采用獨(dú)狼視場(chǎng)機(jī)制和自適應(yīng)增強(qiáng)函數(shù)來優(yōu)化蟻群的尋優(yōu)能力.文獻(xiàn)[13]通過利用零點(diǎn)定理,提出了一種不均衡分配的初始信息素方法,避免了蟻群在搜索過程中過于盲目的情況,使算法的搜索效率得到明顯的提高.文獻(xiàn)[14]通過引入一種動(dòng)態(tài)分組協(xié)作算法,該算法同時(shí)結(jié)合了蟻群系統(tǒng)和最大最小螞蟻系統(tǒng),形成了一個(gè)異構(gòu)的多種群結(jié)構(gòu),每個(gè)種群可以實(shí)現(xiàn)相互進(jìn)化,相互補(bǔ)充,從而顯著的提高了算法的整體性能.文獻(xiàn)[15]提出了一種具有懲罰性措施的蟻群算法,利用懲罰策略對(duì)最壞路徑的信息素濃度進(jìn)行懲罰,通過信息素的揮發(fā)降低螞蟻遍歷最壞路徑的概率,引導(dǎo)螞蟻探索其他未知區(qū)域,提升了算法的全局搜索能力.文獻(xiàn)[16]通過在原有算法的基礎(chǔ)上采用了多步搜索策略來代替單步搜索策略的方法,并對(duì)信息素更新機(jī)制進(jìn)行重新設(shè)計(jì),以及對(duì)規(guī)劃出的路徑進(jìn)行平滑處理,使算法的整體性能得到了明顯的提升.

本文對(duì)蟻群算法在復(fù)雜環(huán)境中的問題進(jìn)行了如下改進(jìn):1)通過在啟發(fā)函數(shù)中引入一種自適應(yīng)調(diào)整的放大因子,使相鄰節(jié)點(diǎn)的啟發(fā)信息差異得到增大,增加了螞蟻選擇最優(yōu)路徑的可能性;2)采用一種獎(jiǎng)懲機(jī)制更新路徑上的信息素,可以在很大程度上提高算法的收斂性;3)對(duì)信息素?fù)]發(fā)因子采用動(dòng)態(tài)調(diào)整的方法來提高蟻群的搜索速度,使算法快速收斂;4)對(duì)改進(jìn)算法生成的路徑進(jìn)行優(yōu)化處理,提高了路徑的平滑性.

1 環(huán)境模型

在研究路徑規(guī)劃的過程中,需要選擇狀態(tài)空間描述方法來建立環(huán)境模型.本文采用柵格法[7,17]來進(jìn)行環(huán)境建模.柵格法的工作原理是假定機(jī)器人運(yùn)動(dòng)的環(huán)境是在一個(gè)二維空間,就可以將這個(gè)空間劃分為許多大小相同的單元.可以根據(jù)柵格中是否存在障礙物來對(duì)柵格的狀態(tài)進(jìn)行判斷.若柵格中存在障礙物,則對(duì)應(yīng)的柵格狀態(tài)為1;否則,對(duì)應(yīng)的柵格狀態(tài)為0.柵格地圖如圖1(a)所示.白色部分為無障礙物的柵格,機(jī)器人可以向其移動(dòng),黑色部分為有障礙物的柵格,機(jī)器人不能向其移動(dòng).如果將機(jī)器人看做一個(gè)質(zhì)點(diǎn),當(dāng)周圍沒有障礙物存在時(shí),8個(gè)方向都可以滿足機(jī)器人的運(yùn)動(dòng)要求,機(jī)器人的運(yùn)動(dòng)方向如圖1(b)所示.

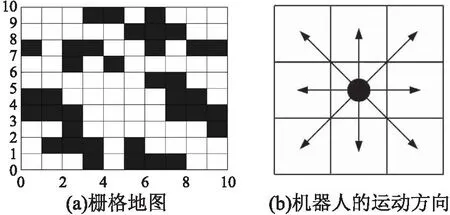
圖1 柵格環(huán)境模型Fig.1 Raster environment model

2 傳統(tǒng)蟻群算法

蟻群算法是一種比較典型的啟發(fā)式搜索算法,螞蟻可以本能地找到從某一點(diǎn)到食物來源的路徑.在t時(shí)刻,第k只螞蟻從節(jié)點(diǎn)i移動(dòng)到節(jié)點(diǎn)j的概率轉(zhuǎn)移公式如下:

(1)

(2)

式中,τij(t)為信息素濃度,α為信息素啟發(fā)因子,β為期望啟發(fā)因子,ηij(t)為啟發(fā)函數(shù).allowedk為路徑搜索所有下一可達(dá)節(jié)點(diǎn)的集合.dij為當(dāng)前節(jié)點(diǎn)i和待選節(jié)點(diǎn)j之間的歐氏距離.

在完成一次迭代后,螞蟻會(huì)在路徑上留下信息素,路徑上原有的信息素會(huì)得到改變.信息素更新公式如下:

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(3)

(4)

(5)

3 蟻群算法改進(jìn)

3.1 啟發(fā)函數(shù)的設(shè)計(jì)

傳統(tǒng)蟻群算法的啟發(fā)函數(shù)通常只取相鄰節(jié)點(diǎn)距離的倒數(shù),由此忽略了待選節(jié)點(diǎn)與目標(biāo)節(jié)點(diǎn)之間的距離,這使得螞蟻在進(jìn)行路徑選擇時(shí)傾向于選擇距離當(dāng)前節(jié)點(diǎn)最近的節(jié)點(diǎn).當(dāng)螞蟻無法搜索到最優(yōu)路徑時(shí),就會(huì)發(fā)生死鎖的狀況.于是,本文不僅考慮了待選節(jié)點(diǎn)與目標(biāo)節(jié)點(diǎn)的距離,還引入起始節(jié)點(diǎn)到待選節(jié)點(diǎn)的距離.由于相鄰節(jié)點(diǎn)距離差異較小,對(duì)整體的啟發(fā)信息影響不算明顯.為此,本文采用一種隨迭代次數(shù)自適應(yīng)變化的放大系數(shù).算法前期,使得相鄰柵格的啟發(fā)信息差異得到明顯增大,在很大程度上增加了螞蟻選擇最優(yōu)路徑的可能性.算法后期,可以減小啟發(fā)信息帶來的影響,有效的避免了局部最優(yōu)情況的發(fā)生.對(duì)應(yīng)的改進(jìn)公式如下:

(6)

(7)

式中,djg為待選節(jié)點(diǎn)和目標(biāo)節(jié)點(diǎn)之間的歐式距離,dSj為起始節(jié)點(diǎn)和待選節(jié)點(diǎn)之間的歐氏距離,N為當(dāng)前迭代次數(shù),Nmax為最大迭代次數(shù).

3.2 改進(jìn)信息素更新策略

傳統(tǒng)的信息素更新策略是在一次迭代結(jié)束后,將那些到達(dá)目標(biāo)點(diǎn)的螞蟻找出來,并在它們所經(jīng)過的路徑上增加信息素.但是,這種情況下,如果給那些劣質(zhì)螞蟻?zhàn)哌^的路徑增加信息素,就會(huì)影響到后續(xù)迭代中的螞蟻.于是,本文采用一種獎(jiǎng)懲機(jī)制[18]來更新路徑上的信息素,即對(duì)最優(yōu)路徑上的信息素采取獎(jiǎng)勵(lì)的措施,對(duì)最差路徑上的信息素采取懲罰的措施,從而使算法快速收斂.對(duì)應(yīng)的信息素更新策略的改進(jìn)公式如下:

(8)

(9)

式中,Lb和Lw為當(dāng)前迭代中最優(yōu)路徑和最差路徑的長(zhǎng)度,Lave為當(dāng)前迭代中的平均路徑長(zhǎng)度,Lk為本次迭代第k只螞蟻?zhàn)哌^的路徑長(zhǎng)度,ψ、φ為權(quán)重系數(shù).

3.3 改進(jìn)信息素?fù)]發(fā)因子

由于路徑規(guī)劃的特殊性,不同階段對(duì)信息素?fù)]發(fā)因子ρ的取值要求也不一樣.ρ過大會(huì)出現(xiàn)路徑上信息素?fù)]發(fā)較快的情況,不利于算法收斂.反之,隨著時(shí)間的增加,信息素會(huì)被大量積累,就會(huì)出現(xiàn)算法陷于局部最優(yōu)的情況.于是綜合以上情況,本文采用一種動(dòng)態(tài)調(diào)整的方法來改進(jìn)ρ.在算法初始階段,給ρ設(shè)定一個(gè)較大的值來加大搜索范圍;在后續(xù)過程中,采用不斷減小ρ的方式來加快算法的收斂速度.對(duì)應(yīng)的改進(jìn)公式如下:

(10)

式中,ρmax和ρmin為信息素?fù)]發(fā)因子的最大值和最小值.

3.4 路徑優(yōu)化策略

3.4.1 拐點(diǎn)優(yōu)化算法

為了減少路徑中的冗余節(jié)點(diǎn),本文引入了一種拐點(diǎn)優(yōu)化算法,該算法可以在很大程度上將路徑長(zhǎng)度和平滑度進(jìn)行優(yōu)化.

拐點(diǎn)優(yōu)化算法的過程如下:在一條起點(diǎn)到目標(biāo)點(diǎn)的路徑中,節(jié)點(diǎn)間的連線不經(jīng)障礙物,則連接下一節(jié)點(diǎn),直到與障礙物相交,將起點(diǎn)與臨近的那個(gè)未穿越障礙物的節(jié)點(diǎn)相連接,并將該節(jié)點(diǎn)作為新的起點(diǎn),直至所選節(jié)點(diǎn)與目標(biāo)點(diǎn)重合才算完成整個(gè)優(yōu)化過程.如圖2(a)所示,初始路徑為S→A→B→C→D→G,經(jīng)過拐點(diǎn)優(yōu)化處理后的路徑為S→B→C→G.由此可見,經(jīng)過拐點(diǎn)優(yōu)化,路徑節(jié)點(diǎn)更少,路徑長(zhǎng)度更短.

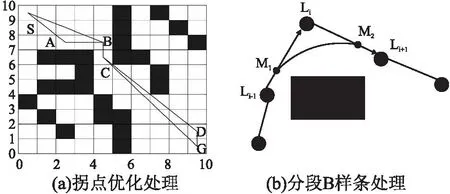
圖2 路徑優(yōu)化處理Fig.2 Path optimization processing

3.4.2 分段B樣條曲線

為了進(jìn)一步改善路徑的平滑性,引入分段B樣條曲線[19]對(duì)拐點(diǎn)優(yōu)化算法所生成的路徑進(jìn)行進(jìn)一步的優(yōu)化處理.采用分段B樣條曲線可以更好地滿足機(jī)器人在柵格環(huán)境下的運(yùn)動(dòng)要求,在一定程度上減少了機(jī)器人與障礙物發(fā)生碰撞的可能性.

由u+1個(gè)控制點(diǎn)Hi和一個(gè)結(jié)點(diǎn)向量n定義的B樣條曲線,公式為:

(11)

式中Fi,k(n)是基于B樣條的函數(shù),下面是遞歸公式:

(12)

(13)

分段B樣條對(duì)原始路徑每個(gè)轉(zhuǎn)折點(diǎn)附近的路徑進(jìn)行平滑處理.分段B樣條處理結(jié)果如圖2(b)所示.Li-1→Li→Li+1表示未經(jīng)處理的路徑,Li為路徑上面的轉(zhuǎn)折點(diǎn),Li附近的路徑需要進(jìn)行平滑處理.

M1Li=M2Li

(14)

在Li-1Li上取一點(diǎn)M1,同時(shí)在LiLi+1上面取一點(diǎn)M2,M1M2為優(yōu)化后的曲線,在這里對(duì)轉(zhuǎn)折點(diǎn)兩側(cè)選定同樣長(zhǎng)度的線段進(jìn)行優(yōu)化處理,具體選取的線段長(zhǎng)度根據(jù)具體的實(shí)驗(yàn)環(huán)境而定.

3.5 本文算法的步驟

步驟1.柵格法建模,并對(duì)算法中所用到的各個(gè)參數(shù)進(jìn)行初始化設(shè)置;

步驟2.將m只螞蟻放在起始點(diǎn),并將該點(diǎn)加入禁忌表;

步驟3.利用式(6)計(jì)算啟發(fā)函數(shù)并用轉(zhuǎn)輪賭法來選擇下一節(jié)點(diǎn),并更新禁忌表;

步驟4.若螞蟻抵達(dá)目標(biāo)點(diǎn),則進(jìn)入步驟5,否則回到步驟3;

步驟5.若螞蟻達(dá)到m只,則進(jìn)入步驟6,否則回到步驟2;

步驟6.利用式(8)更新路徑上的信息素;

步驟7.若滿足N=Nmax,則進(jìn)入步驟8,否則回到步驟2;

步驟8.利用拐點(diǎn)優(yōu)化算法和分段B樣條曲線對(duì)規(guī)劃出的初始路徑進(jìn)行平滑處理,輸出最終結(jié)果.

4 仿真與分析

為了充分驗(yàn)證本文算法的有效性,選用了3種不同規(guī)模的地圖來進(jìn)行機(jī)器人路徑規(guī)劃的仿真實(shí)驗(yàn),分別是20×20規(guī)模、30×30規(guī)模和40×40規(guī)模的柵格地圖.考慮到本文所研究的算法與其他文獻(xiàn)中的算法在參數(shù)的數(shù)值設(shè)置方面存在著一定程度上的差異,為此這里直接引用原始文獻(xiàn)中的實(shí)驗(yàn)數(shù)據(jù)來進(jìn)行仿真實(shí)驗(yàn)上的對(duì)比分析[20].并且考慮到算法運(yùn)行時(shí)間這個(gè)指標(biāo)在很大程度上與計(jì)算機(jī)所對(duì)應(yīng)的處理器的性能有關(guān)聯(lián),這里引用文獻(xiàn)[21]實(shí)驗(yàn)中不同實(shí)驗(yàn)設(shè)備等效耗時(shí)的思想,將原文文獻(xiàn)中的時(shí)間與本文算法中的運(yùn)行時(shí)間進(jìn)行比例換算,即根據(jù)原文文獻(xiàn)設(shè)備得出的算法運(yùn)行時(shí)間,通過換算得到原文文獻(xiàn)在本文設(shè)備中的算法運(yùn)行時(shí)間.通過這種方法有效的解決了不同實(shí)驗(yàn)設(shè)備在時(shí)間指標(biāo)上存在差異的情況,在一定程度上使實(shí)驗(yàn)的數(shù)據(jù)結(jié)果變得真實(shí)可靠.同時(shí)為了便于實(shí)驗(yàn)的對(duì)比分析,4.1、4.2和4.3所用到的實(shí)驗(yàn)參數(shù)會(huì)與公共參數(shù)存在略微差異,這里為了使Nmax和m這兩個(gè)實(shí)驗(yàn)參數(shù)盡可能的與原文文獻(xiàn)保持一致,最大程度上保證實(shí)驗(yàn)上的嚴(yán)謹(jǐn)性,后面實(shí)驗(yàn)中就不再對(duì)修改實(shí)驗(yàn)參數(shù)這項(xiàng)進(jìn)行更多的說明.實(shí)驗(yàn)運(yùn)行環(huán)境為:Windows11 64 bit;Matlab R2021a;處理器Intel(R)Core(TM)i5-1135G7 @ 2.40GHz;內(nèi)存16GB.本文實(shí)驗(yàn)設(shè)計(jì)中所用的公共參數(shù)是根據(jù)許多次的的實(shí)驗(yàn)分析所得出的,這里采用多次實(shí)驗(yàn)的方式來找出滿足實(shí)驗(yàn)最優(yōu)結(jié)果的最佳參數(shù)值.實(shí)驗(yàn)公共參數(shù)如表1所示.

表1 實(shí)驗(yàn)公共參數(shù)Table 1 Experimental public parameters

4.1 20×20仿真環(huán)境

在20×20規(guī)模的地圖環(huán)境下,將本文算法與傳統(tǒng)蟻群算法,文獻(xiàn)[22]算法進(jìn)行仿真實(shí)驗(yàn).實(shí)驗(yàn)參數(shù):m=30,其他參數(shù)與表1相同.3種算法規(guī)劃的路徑如圖3(a)所示,其中帶圓圈標(biāo)記的細(xì)實(shí)線為傳統(tǒng)蟻群算法規(guī)劃的路徑,細(xì)實(shí)線為文獻(xiàn)[22]算法規(guī)劃的路徑,粗實(shí)線為本文算法規(guī)劃的路徑;收斂曲線對(duì)比如圖3(b)所示;實(shí)驗(yàn)結(jié)果對(duì)比如表2所示.從實(shí)驗(yàn)結(jié)果可以看出,本文算法的路徑長(zhǎng)度要優(yōu)于其他兩種算法,可見本文算法具有很強(qiáng)的搜索能力,能夠搜索到較優(yōu)的路徑.并且本文算法的路徑更加平滑,表明在經(jīng)過拐點(diǎn)優(yōu)化算法與分段B樣條曲線的優(yōu)化處理后,路徑的平滑性有了進(jìn)一步的提高.通過圖3(b)可以很明顯的看出,本文算法要比其他兩種算法更快的找到最優(yōu)路徑,收斂于最優(yōu)解.在程序運(yùn)行時(shí)間方面,本文算法和文獻(xiàn)[22]算法差別不大,相比傳統(tǒng)蟻群算法則有著較大的改進(jìn).顯然,本文的改進(jìn)算法在20×20規(guī)模的地圖環(huán)境下,相比較其他兩種算法路徑更優(yōu),算法的收斂性更強(qiáng),搜索路徑的效率更高.

表2 實(shí)驗(yàn)結(jié)果對(duì)比Table 2 Comparison of experimental results

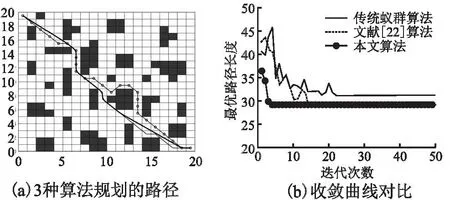
圖3 路徑規(guī)劃結(jié)果Fig.3 Path planning results

4.2 30×30仿真環(huán)境

在30×30規(guī)模的地圖環(huán)境下,利用兩個(gè)不同的地圖環(huán)境,進(jìn)行兩組不同的對(duì)比實(shí)驗(yàn).

4.2.1 實(shí)驗(yàn)1

將本文算法與傳統(tǒng)蟻群算法,文獻(xiàn)[13]算法進(jìn)行仿真實(shí)驗(yàn).3種算法規(guī)劃的路徑如圖4(a)所示,其中帶圓圈標(biāo)記的細(xì)實(shí)線為傳統(tǒng)蟻群算法規(guī)劃的路徑,細(xì)實(shí)線為文獻(xiàn)[13]算法規(guī)劃的路徑,粗實(shí)線為本文算法規(guī)劃的路徑;收斂曲線對(duì)比如圖4(b)所示;實(shí)驗(yàn)結(jié)果對(duì)比如表3所示.從實(shí)驗(yàn)結(jié)果可以看出,本文算法搜索到的路徑長(zhǎng)度更短,路徑更加平滑,搜索到的路徑也更加符合機(jī)器人的行走路線,而傳統(tǒng)蟻群算法和文獻(xiàn)[13]算法路徑長(zhǎng)度還需要得到進(jìn)一步的優(yōu)化,特別的就傳統(tǒng)蟻群算法而言,由于算法搜索路徑的效率較低,以及路徑搜索中難以避免的陷入局部最優(yōu)解的情況,所生成的路線過于差,不能很好的滿足機(jī)器人的行走要求.程序運(yùn)行時(shí)間方面,本文算法要稍遜于文獻(xiàn)[13]算法,相比較傳統(tǒng)蟻群算法仍然存在著明顯的提高.根據(jù)圖4(b)可以很明顯的看出,本文算法在收斂速度上要優(yōu)于另外兩種算法,并且所對(duì)應(yīng)的收斂曲線并沒有存在什么波動(dòng),整體更加平穩(wěn),同時(shí)根據(jù)收斂曲線可以很清楚地看出,本文算法要更早的達(dá)到穩(wěn)定效果.至于與文獻(xiàn)[13]算法在時(shí)間方面的不足可以進(jìn)行舍棄,以得到路徑長(zhǎng)度和收斂速度上的提升.綜合以上可以得出,本文算法得到的的路徑相對(duì)于其他兩種算法而言,路徑更優(yōu),同時(shí)收斂速度更快.

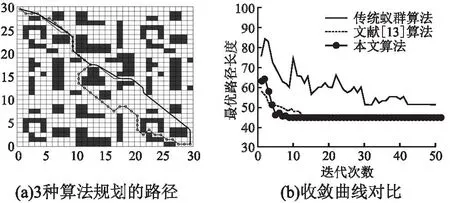
圖4 路徑規(guī)劃結(jié)果Fig.4 Path planning results

4.2.2 實(shí)驗(yàn)2

將本文算法與傳統(tǒng)蟻群算法,文獻(xiàn)[23]算法進(jìn)行仿真實(shí)驗(yàn).實(shí)驗(yàn)參數(shù):Nmax=150,m=100,其他參數(shù)與表1相同.3種算法規(guī)劃的路徑如圖5(a)所示,其中帶圓圈標(biāo)記的細(xì)實(shí)線為傳統(tǒng)蟻群算法規(guī)劃的路徑,細(xì)實(shí)線為文獻(xiàn)[23]算法規(guī)劃的路徑,粗實(shí)線為本文算法規(guī)劃的路徑;收斂曲線對(duì)比如圖5(b)所示;實(shí)驗(yàn)結(jié)果對(duì)比如表4所示.從實(shí)驗(yàn)結(jié)果可以看出,由于本文算法高效的搜索能力以及拐點(diǎn)優(yōu)化算法和分段B樣條曲線先后兩次優(yōu)化處理,使得本文算法在路徑長(zhǎng)度上優(yōu)于文獻(xiàn)[23]算法和傳統(tǒng)蟻群算法.根據(jù)圖5(b)可知,傳統(tǒng)蟻群算法和文獻(xiàn)[23]算法都存在著較明顯的波動(dòng),而本文算法基本沒什么波動(dòng),整體來看較為平穩(wěn).同時(shí),本文算法在收斂速度上相對(duì)于另外的兩種算法明顯更快.表明,本文算法的改進(jìn)策略可以使算法的收斂速度得到明顯的提高.因此,本文算法相比其他兩種算法,具有搜索能力強(qiáng)和快速收斂的特點(diǎn).

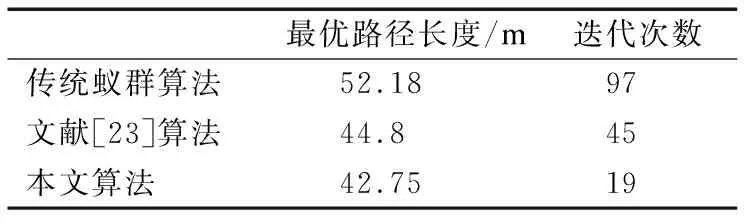
表4 實(shí)驗(yàn)結(jié)果對(duì)比Table 4 Comparison of experimental results

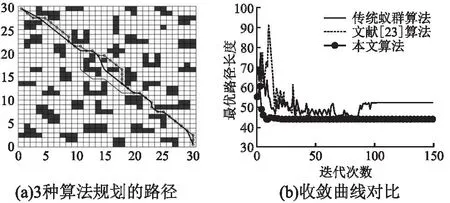
圖5 路徑規(guī)劃結(jié)果Fig.5 Path planning results

4.3 40×40仿真環(huán)境

在40×40規(guī)模的地圖環(huán)境下,將本文算法與文獻(xiàn)[23]算法,傳統(tǒng)蟻群算法進(jìn)行仿真實(shí)驗(yàn).實(shí)驗(yàn)參數(shù):Nmax=400,m=100,其他參數(shù)與表1相同.3種算法規(guī)劃的路徑如圖6(a)所示,其中帶圓圈標(biāo)記的細(xì)實(shí)線為傳統(tǒng)蟻群算法規(guī)劃的路徑,細(xì)實(shí)線為文獻(xiàn)[23]算法規(guī)劃的路徑,粗實(shí)線為本文算法規(guī)劃的路徑;收斂曲線對(duì)比如圖6(b)所示;實(shí)驗(yàn)結(jié)果對(duì)比如表5所示.從實(shí)驗(yàn)結(jié)果可以看出,本文算法經(jīng)過前期的改進(jìn)以及后面拐點(diǎn)優(yōu)化算法和分段B樣條曲線的優(yōu)化處理,所規(guī)劃的路徑更加平滑,也符合機(jī)器人的行走路線.文獻(xiàn)[23]算法和傳統(tǒng)蟻群算法的路徑長(zhǎng)度要高于本文算法,整體上還需要進(jìn)一步的提高.從圖6(b)可知,傳統(tǒng)蟻群算法在前期存在十分明顯的波動(dòng)情況,只是隨著迭代的增加這種波動(dòng)情況開始逐漸減小,直至穩(wěn)定.文獻(xiàn)[23]算法同樣前期存在著較大的波動(dòng),后面才得到明顯的降低,迭代到一定程度才穩(wěn)定下來.而本文算法幾乎沒有存在波動(dòng)的情況,整體比較平穩(wěn),說明本文算法的收斂效果較為明顯.由此可見,本文算法在規(guī)模大,環(huán)境復(fù)雜度高的地圖中,仍然存在著很大的優(yōu)勢(shì).

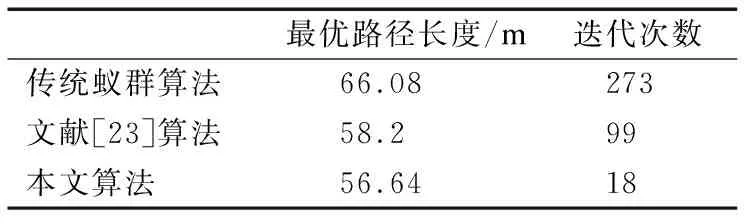
表5 實(shí)驗(yàn)結(jié)果對(duì)比Table 5 Comparison of experimental results

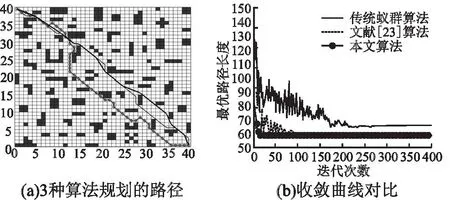
圖6 路徑規(guī)劃結(jié)果Fig.6 Path planning results

5 結(jié) 論

本文提出了一種改進(jìn)蟻群算法的路徑規(guī)劃研究方法,來解決機(jī)器人在復(fù)雜環(huán)境下的路徑規(guī)劃問題.該方法在啟發(fā)函數(shù)中引入動(dòng)態(tài)調(diào)整的放大因子,來增大相鄰節(jié)點(diǎn)的啟發(fā)信息差異,從而增加螞蟻選擇最優(yōu)路徑的概率;采用一種獎(jiǎng)懲機(jī)制更新路徑上的信息素,使算法的收斂速度得到加快;通過動(dòng)態(tài)調(diào)整信息素?fù)]發(fā)因子,加快了算法的收斂速度;在最優(yōu)路徑的基礎(chǔ)上進(jìn)行路徑優(yōu)化,改善了路徑的平滑性,更好的滿足機(jī)器人在柵格環(huán)境下的運(yùn)動(dòng)要求.實(shí)驗(yàn)研究表明,本文改進(jìn)的算法能夠應(yīng)用在規(guī)模性大,復(fù)雜度高的地圖環(huán)境中,并且在一定程度上有著較高的實(shí)用意義.由于本文研究主要是在靜態(tài)環(huán)境下進(jìn)行的,下一步研究可以將路徑規(guī)劃應(yīng)用在動(dòng)態(tài)環(huán)境領(lǐng)域.