移動(dòng)邊緣網(wǎng)絡(luò)中的多目標(biāo)緩存優(yōu)化方法
吳 越,薛釗煜,郭婉婉,崔志華
(太原科技大學(xué) 計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,太原 030024)
0 引 言
隨著信息技術(shù)的快速發(fā)展,各種社交媒體、視頻網(wǎng)站的發(fā)展十分迅速,用戶量快速增長(zhǎng),大量的網(wǎng)絡(luò)通信流量對(duì)基站造成了巨大的壓力.基于移動(dòng)邊緣計(jì)算(MEC)的緩存方法利用邊緣網(wǎng)絡(luò)靠近用戶的特點(diǎn)和感知與存儲(chǔ)能力,將數(shù)據(jù)放置于靠近用戶的邊緣節(jié)點(diǎn)上,能夠有效降低網(wǎng)絡(luò)負(fù)載、提升服務(wù)質(zhì)量.但是在邊緣網(wǎng)絡(luò)環(huán)境中,每個(gè)邊緣節(jié)點(diǎn)的可用緩存空間十分有限,因此如何合理的利用有限的緩存空間將流行度更高的內(nèi)容放置于合適的位置成為了關(guān)鍵問題.
為了提高M(jìn)EC緩存的性能,研究人員做出了許多工作.文獻(xiàn)[1,2]使用基于貝葉斯的流行內(nèi)容預(yù)測(cè)來制定緩存預(yù)取方案;文獻(xiàn)[3]將存儲(chǔ)資源和計(jì)算資源推到網(wǎng)絡(luò)邊緣,基于長(zhǎng)短期記憶(LSTM)神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)內(nèi)容流行度,將預(yù)測(cè)結(jié)果應(yīng)用于緩存方案的制定;文獻(xiàn)[4]基于博弈論的思想將邊緣網(wǎng)絡(luò)中的節(jié)點(diǎn)看做博弈者,決定自身的緩存策略來達(dá)到最大緩存收益,在博弈中達(dá)到納什均衡并據(jù)此設(shè)計(jì)了一種分布式均衡算法;文獻(xiàn)[5]基于多臂強(qiáng)盜方法設(shè)計(jì)的解決如何估計(jì)未知用戶偏好,并提出了一種基于多智能體擴(kuò)展單抗的解決方案,實(shí)現(xiàn)了分散的緩存放置策略;文獻(xiàn)[6]使用神經(jīng)網(wǎng)絡(luò)模型預(yù)測(cè)未來可能的用戶請(qǐng)求,并通過聯(lián)合優(yōu)化延遲和能耗來制定緩存方案;文獻(xiàn)[7]使用Zipf定律估計(jì)用戶偏好,將目標(biāo)建模為延遲最優(yōu),提出了基于改進(jìn)KM(Kuhn-Munkres)的內(nèi)容放置方法;文獻(xiàn)[8]從服務(wù)運(yùn)營(yíng)商的角度將數(shù)據(jù)緩存問題表述為一個(gè)約束優(yōu)化問題,優(yōu)化目標(biāo)位延遲最低,用整數(shù)規(guī)劃的方法來解決優(yōu)化問題;文獻(xiàn)[9]結(jié)合了基于長(zhǎng)短期記憶(LSTM)的局部學(xué)習(xí)和基于集成的元學(xué)習(xí)來提高預(yù)測(cè)性能繼而提高緩存命中率.以上研究主要針對(duì)估計(jì)用戶偏好,根據(jù)估計(jì)的用戶偏好進(jìn)行緩存決策,雖然能夠提高緩存性能,但考慮緩存問題的角度單一,不能滿足多樣化的緩存需求.
針對(duì)復(fù)雜的緩存需求,文獻(xiàn)[10]將RAN建模為一個(gè)區(qū)域,通過劃分區(qū)域的方式簡(jiǎn)化問題,將緩存問題表述為一個(gè)混合整數(shù)線性規(guī)劃模型,文獻(xiàn)[11]同樣使用區(qū)域劃分的方式建模,提出基于博弈論的緩存放置策略;文獻(xiàn)[12,13]從服務(wù)提供商的角度考慮,在滿足訪問延遲約束的前提下最大化服務(wù)提供商的利益;文獻(xiàn)[14-16]使用數(shù)據(jù)訪問計(jì)數(shù)、數(shù)據(jù)訪問頻率和數(shù)據(jù)大小作為優(yōu)化目標(biāo)的多目標(biāo)優(yōu)化數(shù)據(jù)緩存模型,結(jié)合了蟻群算法和遺傳算法進(jìn)行求解;文獻(xiàn)[17]為了克服緩存污染問題,提出了LRU-GENACO,該方法結(jié)合了LRU、ACO和GA算法,其中LRU算法被分配用于解決緩存污染問題,而混合ACO-GA在緩存數(shù)據(jù)被消除之前優(yōu)化緩存數(shù)據(jù)選擇;[18]使用評(píng)估的緩存值、數(shù)據(jù)對(duì)象獲取和替換成本將緩存放置問題建模,使用禁忌搜索算法求解模型;文獻(xiàn)[19]提出了一種基于貪心算法的云邊緣協(xié)同緩存模型和相應(yīng)算法,以降低負(fù)載提高緩存命中率;文獻(xiàn)[20]提出了歸一化布谷鳥搜索算法聯(lián)合優(yōu)化延遲、功耗、連接成功率;文獻(xiàn)[21]基于博弈論的思想研究了聯(lián)合優(yōu)化中如何公平的處理具有競(jìng)爭(zhēng)關(guān)系的優(yōu)化目標(biāo),將QoE和能量效率作為博弈對(duì)象,置于納什均衡模型中,并提出了一個(gè)公平的多回合博弈算法;文獻(xiàn)[22]提出了一種基于多臂強(qiáng)化學(xué)習(xí)的實(shí)用感知協(xié)作服務(wù)緩(UACSC)方案,以協(xié)調(diào)多個(gè)邊緣服務(wù)器以做出動(dòng)態(tài)聯(lián)合緩存決策,在最小化緩存成本的同時(shí)優(yōu)化服務(wù)延遲.文獻(xiàn)[23]將STP和平均傳輸延遲建模為一個(gè)多目標(biāo)優(yōu)化問題,以最大化STP或最小化延遲為目標(biāo),并建立了多目標(biāo)緩存布局優(yōu)化問題.提出了一種新的投影多目標(biāo)杜鵑搜索算法(PMOCSA),以獲得最優(yōu)緩存布局的解決方案.上述研究考慮了多樣化的緩存需求,大部分通過將多目標(biāo)轉(zhuǎn)化為單目標(biāo)的方式聯(lián)合優(yōu)化,然而多個(gè)目標(biāo)之間的關(guān)系難以區(qū)分、不易比較,不同目標(biāo)的權(quán)重參數(shù)確定方式十分主觀,尤其是目標(biāo)之間互相沖突時(shí)會(huì)使加權(quán)目標(biāo)函數(shù)的結(jié)構(gòu)十分復(fù)雜,權(quán)重參數(shù)需要在優(yōu)化開始前確定,在迭代過程中無法干預(yù),這使得優(yōu)化結(jié)果難以使人滿意.
綜上本文站在不同的角度觀察MEC緩存方案得到了不同的需求[24]:用戶希望能在更短的時(shí)間內(nèi)得到響應(yīng)獲得所訪問的內(nèi)容;網(wǎng)絡(luò)提供商希望使得邊緣節(jié)點(diǎn)的負(fù)載盡可能地低,緩存效率更高;服務(wù)提供商則希望降低緩存成本的支出.為了使多個(gè)利益相關(guān)方均能收益,提升系統(tǒng)整體性能,本文構(gòu)建了一個(gè)考慮3個(gè)目標(biāo)的邊緣緩存模型,并設(shè)計(jì)了一種基于最遠(yuǎn)交配和淘汰策略的多目標(biāo)進(jìn)化算法(MOEA-FMES).
本文的重要貢獻(xiàn)總結(jié)如下:
1)構(gòu)建了一個(gè)考慮用戶時(shí)延、緩存存儲(chǔ)成本和邊緣節(jié)點(diǎn)傳輸能耗的多目標(biāo)緩存模型,以提高系統(tǒng)的整體性能,使得不同的利益相關(guān)方均能從中收益.
2)為了求解所提出的緩存模型,設(shè)計(jì)了MOEA-FMES,采用基于參考向量的最遠(yuǎn)距離選擇來選擇父代個(gè)體;采用一種基于BDE和歐式距離的動(dòng)態(tài)適應(yīng)度值算子;在環(huán)境選擇中循環(huán)淘汰機(jī)制選出下一代種群.
3)為了驗(yàn)證所提方法的有效性、評(píng)估提出算法,設(shè)計(jì)了模擬仿真試驗(yàn),通過對(duì)比AGEII、IBEA、SPEA/R、NSGAII、VaEA和MOEA-FMES說明了本文提出方法的有效性.
1 模型設(shè)計(jì)
1.1 網(wǎng)絡(luò)模型
邊緣云計(jì)算環(huán)境是多層網(wǎng)絡(luò)架構(gòu),包括云計(jì)算層、邊緣計(jì)算層和終端層.為了能夠更為高效的利用邊緣網(wǎng)絡(luò)資源來提升服務(wù)效率,需要將高流行度的緩存內(nèi)容放置在合適的邊緣節(jié)點(diǎn).不同的放置方案會(huì)產(chǎn)生不同的影響、收益,如前文所述,MEC緩存中的利益相關(guān)方之間互相沖突.
本文考慮如圖1所示的網(wǎng)絡(luò)架構(gòu),包含一個(gè)宏基站(MBS)和M個(gè)小基站(SBS),宏基站通過光纖鏈路與云網(wǎng)絡(luò)連接,通過BS鏈路與SBS連接;每個(gè)SBS與不等數(shù)量的用戶設(shè)備(UE)連接,MBS中存儲(chǔ)整個(gè)內(nèi)容庫(kù),考慮到實(shí)際情況中的內(nèi)容大小不同,本文假設(shè)內(nèi)容庫(kù)包含N個(gè)大小不等的內(nèi)容,記為D={d1,d2,…,dN},內(nèi)容大小服從參數(shù)為α的正態(tài)分布.使用E={e1,e2,…,eM}表示SBS集合,SBS的存儲(chǔ)容量有限,容量大小記為C.將用戶連接的SBS稱為本地SBS,當(dāng)UE所請(qǐng)求的內(nèi)容不在本地SBS中時(shí),可以向一跳友鄰SBS請(qǐng)求內(nèi)容,若一跳友鄰SBS也沒有緩存內(nèi)容時(shí),向MBS請(qǐng)求內(nèi)容,SBS之間的關(guān)聯(lián)情況由Z={zm1,zm2,…,zMM}表示,zmm=1表示互相連接,否則表示不連接,Y={y1,y2,…,yN}表示SBS連接的用戶的數(shù)量的集合,本文假設(shè)在時(shí)隙t內(nèi)Y服從參數(shù)為δ的泊松分布.X={xm1,xm2,…,xmn}表示緩存方案,xmn表示基站em是否緩存內(nèi)容dn,1表示緩存該內(nèi)容,0則表示不緩存該內(nèi)容.
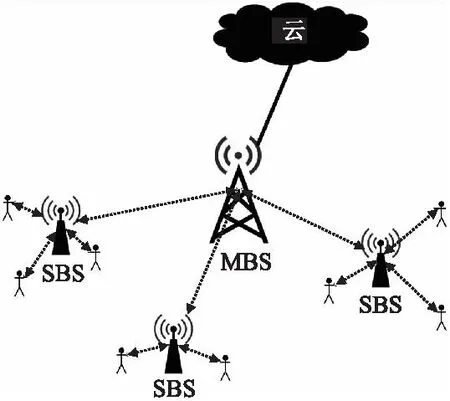
圖1 MEC結(jié)構(gòu)Fig.1 MEC structure
1.2 緩存模型
本文考慮在時(shí)隙t內(nèi)的緩存內(nèi)容放置方案,假設(shè)在時(shí)隙t內(nèi)內(nèi)容的流行度基本穩(wěn)定不變.齊普夫(Zipf)定律被用于估計(jì)內(nèi)容的流行度已經(jīng)被證明了其有效性,許多的研究也基于假設(shè)滿足該定律展開,如文獻(xiàn)[25]證明YouTube上的內(nèi)容流行度服從Zipf分布.因此本文假設(shè)內(nèi)容流行度服從Zipf分布.內(nèi)容庫(kù)中包含N個(gè)內(nèi)容,并按照訪問次數(shù)進(jìn)行降序排序P={p1,p2,…,pN},表示內(nèi)容的請(qǐng)求概率分布,pi表示第i個(gè)內(nèi)容被請(qǐng)求概率,概率值由公式(1)按照Z(yǔ)ipf計(jì)算:
(1)
式中γ為參數(shù)控制分布的密集程度.
SBS、MBS向所連接的設(shè)備發(fā)送數(shù)據(jù)的速率V由公式(2)得出:
(2)
式中y表示所連接的設(shè)備數(shù)量,B為帶寬,Q為平均發(fā)射功率,μ為噪聲功率.SBS的緩存空間大小記為C.
1.3 優(yōu)化目標(biāo)
本文針對(duì)MEC緩存中不同利益方的需求,提出了3個(gè)優(yōu)化目標(biāo),分別為延遲、緩存成本、基站傳輸功耗.當(dāng)用戶請(qǐng)求的內(nèi)容不在本地SBS時(shí),僅向一跳友鄰SBS或MBS發(fā)起請(qǐng)求.因此本文中所計(jì)算的延遲、傳輸功耗需要綜合考慮不同的情況進(jìn)行計(jì)算,即a)請(qǐng)求的內(nèi)容緩存于本地SBS時(shí),直接向用戶返回內(nèi)容;b)請(qǐng)求的內(nèi)容未緩存與本地SBS但緩存于友鄰SBS時(shí),首先將請(qǐng)求的內(nèi)容發(fā)送至本地SBS,再由本地SBS發(fā)送給用戶;c)當(dāng)請(qǐng)求的內(nèi)容本地SBS與友鄰SBS均未緩存時(shí),先由MBS發(fā)送至本地SBS,再由本地SBS發(fā)送給用戶.delay(m)表示某個(gè)SBS所連接用戶的延遲,計(jì)算方式由公式(3)給出.cost(m)表示某個(gè)SBS所緩存的內(nèi)容大小,用于衡量緩存成本計(jì)算方式由公式(4)給出,用于衡量存儲(chǔ)成本,power(m)表示某個(gè)SBS提供服務(wù)時(shí)的傳輸功耗,計(jì)算方式由公式(5)給出.
delay(m)=t1+t2+t3
(3)
(4)
power(m)=Qst1+Qst2+QMt3
(5)
其中t1為情況a下的延遲;t2為情況b下的延遲;t3為情況c下的延遲.
(6)
(7)
(8)
式中BS,BM分別表示SBS和MBS的帶寬,QM,QS分別表示SBS和MBS的平均發(fā)射功率.
那么可以得到3個(gè)互相沖突的目標(biāo),分別是:用戶平均延遲f1,SBS平均緩存成本f2,平均傳輸功耗f3.由于本文考慮的SBS的緩存空間大小有限且一致,故每個(gè)SBS所緩存的內(nèi)容大小必須不大于C.
因此MEC緩存多目標(biāo)優(yōu)化問題可以表述為:
(9)
顯然的,延遲與緩存是否命中相關(guān),節(jié)點(diǎn)緩存的內(nèi)容越多緩存命中的可能性越高將會(huì)使得平均延遲越低,而這將導(dǎo)致緩存成本變高,所以f1與f2互相是沖突的.另外當(dāng)緩存命中時(shí)本地SBS直接向服務(wù)的用戶發(fā)送數(shù)據(jù),而未命中時(shí)則需要友鄰SBS或MBS先向本地SBS發(fā)送數(shù)據(jù)再由本地SBS發(fā)送給服務(wù)的用戶,所以節(jié)點(diǎn)緩存內(nèi)容增加將使得平均傳輸功耗降低,故而f2與f3互相沖突.由于MBS發(fā)射功率高于SBS,因此當(dāng)友鄰節(jié)點(diǎn)緩存了本地所請(qǐng)求的內(nèi)容時(shí)本地SBS無需向MBS請(qǐng)求數(shù)據(jù)從而降低了功耗但相應(yīng)的提高了延遲,因此f1與f3也是互相沖突的.圖2(a)~圖2(c)展示了求解本文時(shí)模型不同目標(biāo)值之間的關(guān)系,通過觀察圖中解的分布也能得出相同的結(jié)論.

圖2 目標(biāo)值關(guān)系圖Fig.2 Objective value relation diagram
2 算法改進(jìn)
上述問題是一個(gè)非凸優(yōu)化問題,進(jìn)化算法是解決大規(guī)模非凸優(yōu)化問題的一種有效方法.再過去的十?dāng)?shù)年中,研究者們提出了多種高性能多目標(biāo)進(jìn)化算法.這些算法的基本一般過程是:1)隨機(jī)生成初始種群并計(jì)算目標(biāo)函數(shù)的值;2)通過交配選擇算子從種群中選擇個(gè)體,以雜交和突變產(chǎn)生后代種群;3)父代和子代種群被合并,下一代種群從環(huán)境選擇算子中選擇;4)重復(fù)上述操作,直到滿足終止條件.其中,匹配選擇算子和環(huán)境選擇算子極大地影響了算法的求解性能.為了更好地平衡分集和收斂,本文提出了MOEA-FMES算法,在匹配選擇時(shí)采取最遠(yuǎn)鄰居結(jié)合的策略來增加多樣性,設(shè)計(jì)了結(jié)合SDE[23]和歐式距離的適應(yīng)度值計(jì)算方式用于環(huán)境選擇算子,以平衡進(jìn)化過程中的收斂性和多樣性,并且環(huán)境選擇還采用了循環(huán)淘汰的方式為下一代種群選擇優(yōu)秀的個(gè)體.
2.1 算法總體描述
為了同時(shí)優(yōu)化本文所提出的3個(gè)目標(biāo)函數(shù),本文提出了MOEA-FMES.如前文所述X表示一個(gè)緩存方案矩陣,表示某個(gè)SBS是否緩存某個(gè)內(nèi)容,因此本文的多目標(biāo)進(jìn)化算法采用二進(jìn)制編碼方式,種群數(shù)量記為L(zhǎng).
多目標(biāo)進(jìn)化算法總體流程如算法1中偽代碼所示.首先進(jìn)行初始化設(shè)置,包括初始化種群,產(chǎn)生L個(gè)個(gè)體;通過混合均勻設(shè)計(jì)方法在單位超平面上精確返回L個(gè)具有M個(gè)目標(biāo)的均勻分布點(diǎn);對(duì)目標(biāo)值進(jìn)行歸一化處理,并將每個(gè)個(gè)體關(guān)聯(lián)到余弦距離最近的參考向量上,從而完成初始種群劃分.然后開始進(jìn)化過程,直到達(dá)到最大迭代次數(shù):計(jì)算參數(shù)θ;根據(jù)匹配選擇算子選擇父代種群;進(jìn)行交叉變異操作產(chǎn)生子代種群;將父代與子代合并,并進(jìn)行歸一化處理;根據(jù)環(huán)境選擇算子選擇最優(yōu)的前L個(gè)個(gè)體作為下一代種群.
算法1.多目標(biāo)進(jìn)化算法框架
輸入:種群數(shù)量L
輸出:最終解集
1.Create an initial parent populationP
2.Generate L reference vectors W according to the MUD method
3.W=MUD()
4.Normalize objectives of members inP
5.P′:= Objective_Normalization (P)
6.Associated reference vector:
7.E(i)=Associate(P′, W)
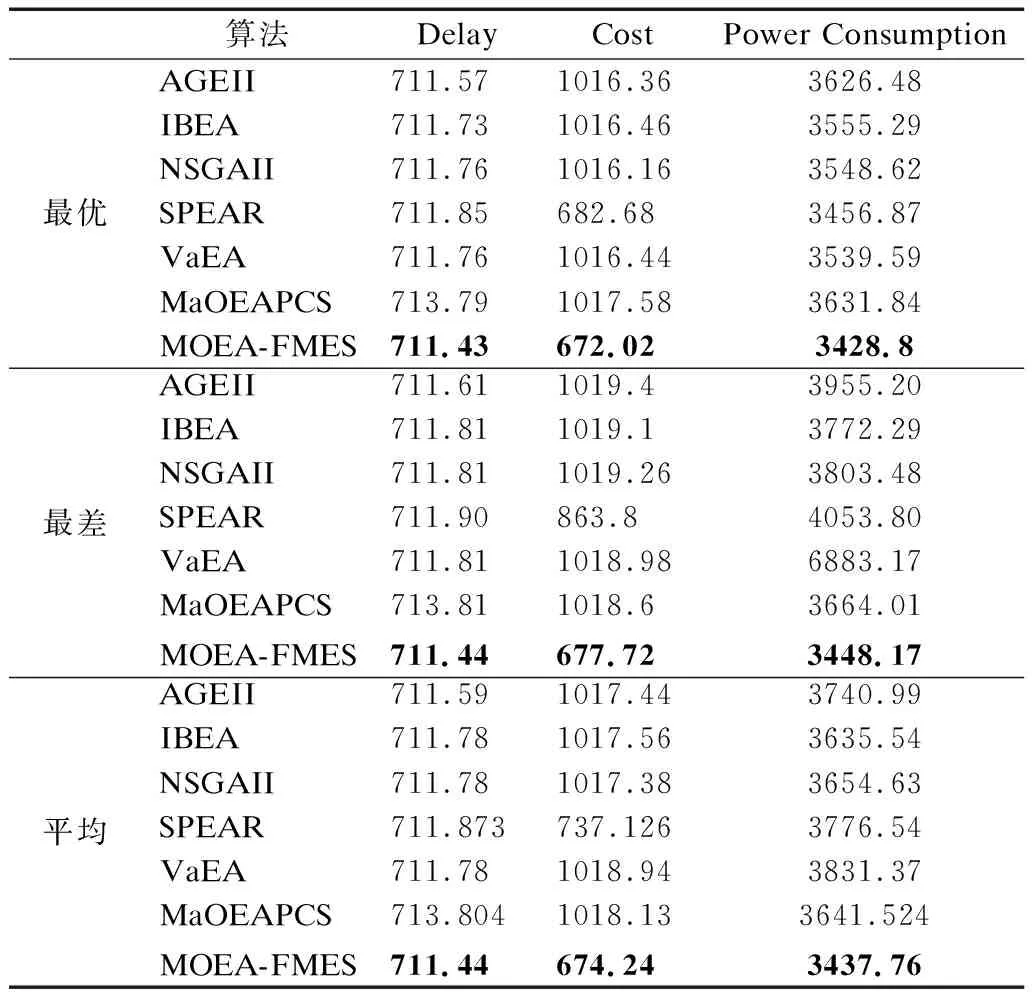
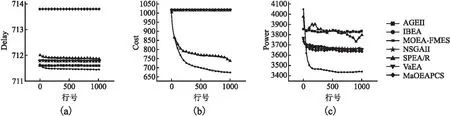
8.while t 9. θ is calculated by Eq.8 10.P=FarthestSelection (W,E(i)) //Select the P by Matching Selection Operator 11. O=GA(P)//The Offspring population O was generated by GA 12.G=P∪O 13.G′=Objective_Normalization(P) 14.P=Environment_Selection(G′,W,θ); 15.end while 匹配選擇的目的是通過高質(zhì)量的父代個(gè)體進(jìn)行交叉、變異,從而產(chǎn)生優(yōu)秀的子代,是進(jìn)化算法的重要組成部分.本文的匹配選擇通過選擇兩個(gè)最遠(yuǎn)子種群中的個(gè)體即余弦距離最遠(yuǎn)的參考向量所關(guān)聯(lián)的個(gè)體來組成父代種群.偽代碼如算法2所示.首先通過使用公式(11)計(jì)算所有參考向量之間的余弦距離: θ=(FE/maxFE)2 (11) 然后開始選擇:從參考向量集中選擇一個(gè)w,隨機(jī)選擇一個(gè)w關(guān)聯(lián)的個(gè)體添加到Parent1中并從當(dāng)前種群中刪去該個(gè)體,選擇w余弦距離最遠(yuǎn)的參考向量w′,之后隨機(jī)選擇一個(gè)w′關(guān)聯(lián)的個(gè)體添加到Parent2中并從當(dāng)前種群中刪去該個(gè)體.循環(huán)結(jié)束后合并Parent1,Parent2. 算法2.匹配選擇 輸入:參考向量W,個(gè)體關(guān)聯(lián)的參考向量集合E(i) 輸出:用于交叉變異的父代種群P 1.Wdis=cosθ(W)//by Eq.(12) 2.while length/(Parent1) 3. for w=W 4. p1=random(E(i)==w) 5. Parent1=[Parent1,p1] 6.w′=max(Wdis(w)) 7. p2=random(E(i)==w) 8. Parent2=[Parent2,p2] 9. end for 10.P=[Parent1, Parent2] 11.end while σ=(FE/maxFE)2 (12) (13) 環(huán)境選擇的目的是從合并后的種群中選擇優(yōu)秀的個(gè)體組成新的種群,新的種群應(yīng)當(dāng)確保個(gè)體之間保持收斂性和多樣性的平衡,從而不斷優(yōu)化種群.在本文的設(shè)計(jì)中,環(huán)境選擇參考了SPEA/R[27].與SPEA/R不同的是:本文替換了適應(yīng)度的計(jì)算方式,且不同于SPEA/R的適應(yīng)度以多樣性優(yōu)先、收斂性第二,本文根據(jù)迭代次數(shù)動(dòng)態(tài)的調(diào)整多樣性與收斂性的關(guān)系;SPEA/R在一個(gè)選擇循環(huán)完成后進(jìn)行下一輪循環(huán),而本文在一個(gè)選擇循環(huán)完成后會(huì)刪去被選擇的個(gè)體并重新評(píng)估剩余個(gè)體再開始下一輪循環(huán). 環(huán)境選擇循環(huán)的從各個(gè)參考向量的關(guān)聯(lián)個(gè)體中進(jìn)行選擇.在每一輪開始時(shí)首先計(jì)算當(dāng)前種群中個(gè)體的適應(yīng)度值,然后從每個(gè)參考向量周圍選擇適應(yīng)度值最小的個(gè)體(求解最小化問題時(shí)),選擇完一輪之后將選擇的個(gè)體添加到下一代種群中并從當(dāng)前種群中刪去,直到新種群的數(shù)量達(dá)到種群數(shù)量L.之所以每選擇一輪就重新計(jì)算剩余個(gè)體的適應(yīng)度值,這是因?yàn)檠h(huán)選擇的目的是均勻的選擇參考向量所劃分的子種群中的優(yōu)秀個(gè)體,以選擇高質(zhì)量的解并提高解的均勻性,而本文在適應(yīng)度的計(jì)算中考慮了個(gè)體之間的密度信息,一輪選擇循環(huán)結(jié)束之后剩余個(gè)體之間的密度信息必然會(huì)發(fā)生變化,因此有必要對(duì)剩余個(gè)體進(jìn)行重新評(píng)估.雖然重新計(jì)算適應(yīng)度增加了計(jì)算量但能夠更好的評(píng)估剩余個(gè)體的優(yōu)劣.環(huán)境選擇的偽代碼如算法3所示. 算法3.環(huán)境選擇 輸入:歸一化目標(biāo)值P′,參考向量W,平衡參數(shù) 輸出:NextP,E 1.E=Associate(P′,W)//Associate reference vector 2.while length(NextP) 3. Fit=(P′,E,σ) 4. for each reference directioni∈W 5. if E(i)≠? 6. q=argminp∈E(i)Fit(p) 7. Save q to H 8. end if 9. end for 10. remove H from P and E 11.end while 為了驗(yàn)證本文提出的MEC緩存方法的有效性,本文基于MATLAB 2022a軟件使用PlatEMO v3.3平臺(tái)進(jìn)行仿真模擬實(shí)驗(yàn),參數(shù)設(shè)置如表1所示,并與5種多目標(biāo)優(yōu)化算法進(jìn)行對(duì)比:AGEII[28]、IBEA[29]、SPEA/R[30]、NSGAII[31]、VaEA[32]、MaOEAPCS[33].為了保證結(jié)果的可靠性,對(duì)比算法的參數(shù)設(shè)置保持默認(rèn)設(shè)置. 表1 仿真參數(shù)表Table 1 Simulation parameter table 本文使用Spacing[34]、IGD[35]來進(jìn)行性能評(píng)價(jià),這兩個(gè)指標(biāo)被廣泛使用的評(píng)估多目標(biāo)優(yōu)化算法,分別用于評(píng)價(jià)算法的解的多樣性、綜合性能. 1)Spacing metric (SP): (14) 2)Inverse generation distance (IGD): (15) P為解集,P′為從前沿面上采樣的一組均勻分布的參考點(diǎn),d(i,j)為參考集中的點(diǎn)i與解集中的點(diǎn)j之間的歐氏距離. 在多目標(biāo)問題中,每個(gè)算法都會(huì)最終給出一組非支配解集,供決策者進(jìn)行決策,解集中的每個(gè)解在不同目標(biāo)上的各有優(yōu)劣. 表2中給出了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES在本文提出的MEC緩存模型上計(jì)算得到的SP、IGD值.表中用黑體著重標(biāo)出了最優(yōu)值,并在每個(gè)數(shù)值的后面用‘+’、‘-’、‘=’標(biāo)注了對(duì)比算法與MOEA-FMES的對(duì)比情況,分別表示優(yōu)于MOEA-FMES、弱于MOEA-FMES和與MOEA-FMES持平.結(jié)果顯示在IGD上MOEA-FMES表現(xiàn)最好,說明MOEA-FMES覆蓋了真實(shí)的帕累托前沿面,能夠給出一組高質(zhì)量的非支配解集,SPEA/R和NSGAII在IGD上較為接近MOEA-FMES,而其他算法表現(xiàn)較差.在SP上,MOEA-FMES表現(xiàn)最好,說明所提出算法的解集最為均勻,種群的多樣性最好,SPEA/R在SP上的表現(xiàn)較為接近MOEA-FMES,而AGEII性能最差,說明其給出的解集分布不均勻,多樣性較差. 表2 評(píng)價(jià)指標(biāo)對(duì)照表Table 2 Comparison table of evaluation indicators 表3中給出了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES對(duì)本文模型上的影響情況.通過對(duì)比不同算法給出的最終解集的不同目標(biāo)值上的最優(yōu)、最差、平均值來評(píng)估算法的優(yōu)劣.可以看出MOEA-FMES在3個(gè)目標(biāo)值上的平均、最優(yōu)和最差表現(xiàn)均優(yōu)于其他算法,表現(xiàn)出了良好的整體性能.具體來說在延遲方面6種算法的表現(xiàn)相似,無論是最優(yōu)、最差還是平均值MOEA-FMES的領(lǐng)先幅度都很小;在緩存成本上MOEA-FMES和SPEA/R在平均、最優(yōu)和最差上對(duì)于其他算法都有明顯優(yōu)勢(shì),且MOEA-FMES均能取得最優(yōu)結(jié)果,說明MOEA-FMES能夠有效的降低緩存成本;在傳輸功耗方面,雖然六種算法的最優(yōu)值和平均值區(qū)別較小,但在最差值上VaEA與其他算法的差距很大,MOEA-FMES在最優(yōu)、最差和平均值上都優(yōu)于其他算法,說明MOEA-FMES能夠有效降低傳輸功耗. 表3 6種算法在3個(gè)目標(biāo)上的目標(biāo)值Table 3 Target values of six algorithms on three targets 圖3中的折線圖顯示了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES求解本文模型的3個(gè)目標(biāo)的收斂情況.本文仿真實(shí)驗(yàn)最大迭代次數(shù)設(shè)為1000,可以看出在前300代收斂速度較快,之后收斂速度不斷放緩,在約900代之后收斂程度基本沒有變化.MOEA-FMES能夠使得3個(gè)目標(biāo)均有效收斂,且表現(xiàn)最好,SPEA/R雖然也能使3個(gè)目標(biāo)共同收斂,但在傳輸功耗上的收斂程度較差,而其他算法則僅能使個(gè)別目標(biāo)收斂,其余目標(biāo)上幾乎不收斂,導(dǎo)致曲線重疊,最終的收斂折線圖直觀上不易觀察到每個(gè)圖像的收斂程度,且收斂程度較低,陷入了局部最優(yōu). 圖3 解集收斂圖Fig.3 Convergence plot of the solution set 圖4中的散點(diǎn)圖顯示了AGEII、IBEA、NSGAII、SPEAR、VaEA、MaOEAPCS和MOEA-FMES求解本文模型得到的解集分布情況,圖中每一個(gè)小球代表一個(gè)解.可以看出SPEA/R的解在空間中的分布呈長(zhǎng)條狀,MaOEAPCS的解集雖然分散較為均勻但最終保留的解個(gè)數(shù)過少,AGEII的解主要分布在空間的上半部分,IBEA、NSGAII、和VaEA的分布范圍較為均勻、接近,MOEA-FMES解在空間中的分布最為均勻,表明解的多樣性較好,在3個(gè)目標(biāo)上均進(jìn)行了有效的探索. 圖4 解集分布圖(a~g分別為AGEII、IBEA、NSGAII、SPEAR、VaEA/MaOEAPCS和MOEA-FMES)Fig.4 Solution set distribution diagram (a~g is AGEII, IBEA, NSGAII, SPEAR, VaEA, MaOEAPCS and MOEA-FMES, respectively) 這是由于MOEA-FMES的環(huán)境選擇在循環(huán)選擇中不斷地重新評(píng)估剩余個(gè)體,動(dòng)態(tài)地調(diào)整收斂性和多樣性的關(guān)系,從而使得選出的個(gè)體具有更好的代表性,在匹配選擇時(shí)從兩個(gè)最遠(yuǎn)子種群中隨機(jī)選擇個(gè)體來組成父代種群,因此MOEA-FMES不僅能夠探索更多的解空間,解集的多樣性更好,還能避免解集陷入局部最優(yōu),使算法更快地收斂且3個(gè)目標(biāo)均能收斂到最優(yōu). 以上分析說明本文提出的MEC緩存模型是合理的,并且本文提出的優(yōu)化算法在求解所提出的緩存模型時(shí)能夠同時(shí)優(yōu)化3個(gè)目標(biāo),最終給出一組收斂性好且分布均勻的非支配解集供決策者選擇. 針對(duì)MEC緩存資源緊張的問題,為了提升系統(tǒng)整體性能,使得各個(gè)利益相關(guān)方均能從MEC中獲益,本文提出了一種兼顧延遲、緩存成本、傳輸能耗的多目標(biāo)緩存模型.為了更好的求解提出的模型,提出了一種基于最遠(yuǎn)交配和淘汰策略的多目標(biāo)進(jìn)化算法(MOEA-FMES),通過從具有最遠(yuǎn)余弦距離的參考向量周圍選擇個(gè)體的方式來選擇父代個(gè)體,通過循環(huán)淘汰機(jī)制從各個(gè)參考向量的關(guān)聯(lián)個(gè)體中進(jìn)行環(huán)境選擇,由于淘汰個(gè)體后會(huì)導(dǎo)致剩余個(gè)體的密度信息發(fā)生改變,所以每一輪選擇開始前需要重新評(píng)估剩余個(gè)體.為了評(píng)估提出的MOEA-FMES,本文進(jìn)行了模擬仿真實(shí)驗(yàn),在IGD、Spacing上均表現(xiàn)優(yōu)秀,并分析了算法的性能.在未來的工作中,將進(jìn)一步完善緩存模型、改進(jìn)算法來提高系統(tǒng)整體性能,如考慮用戶偏好的動(dòng)態(tài)變化;多個(gè)用戶之間的優(yōu)先性;考慮用戶的移動(dòng)對(duì)緩存性能的影響.2.2 匹配選擇
2.3 適應(yīng)度計(jì)算
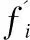
2.4 環(huán)境選擇
3 實(shí)驗(yàn)與總結(jié)
3.1 實(shí)驗(yàn)設(shè)計(jì)

3.2 評(píng)價(jià)指標(biāo)

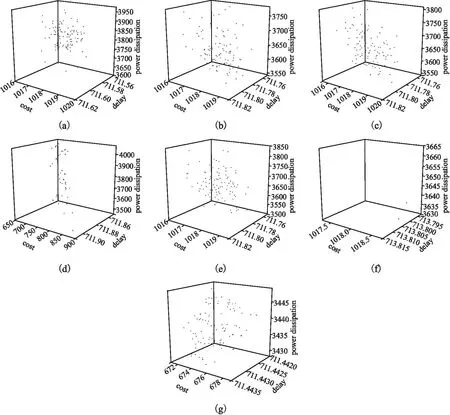
3.3 結(jié)果分析

4 總 結(jié)

