均衡相似程度和緊密程度的局部社區(qū)發(fā)現(xiàn)算法
張霄宏,吳鳳祥,賈會梅,羅軍偉
1(河南理工大學(xué) 計算機科學(xué)與技術(shù)學(xué)院,河南 焦作 454000) 2(河南理工大學(xué) 軟件學(xué)院,河南 焦作 454000) 3(河南中光學(xué)集團有限公司,河南 南陽 473003)
0 引 言
現(xiàn)實世界中的很多系統(tǒng)都能抽象成復(fù)雜網(wǎng)絡(luò)[1].復(fù)雜網(wǎng)絡(luò)往往具有社區(qū)結(jié)構(gòu).同一社區(qū)內(nèi)的節(jié)點連接緊密,不同社區(qū)內(nèi)的節(jié)點連接相對稀疏.研究復(fù)雜網(wǎng)絡(luò)的社區(qū)結(jié)構(gòu)有助于理解網(wǎng)絡(luò)的功能和特性,具有十分重要的理論和應(yīng)用價值[2-5].局部社區(qū)發(fā)現(xiàn)算法因不需要了解網(wǎng)絡(luò)的全局信息、時間復(fù)雜度較低而備受關(guān)注.局部社區(qū)發(fā)現(xiàn)方法可分為局部擴展優(yōu)化[6,7]、派系過濾[8,9]、標簽傳播[10,11]以及局部邊聚類優(yōu)化[12-14]4類.其中,基于局部擴展優(yōu)化的社區(qū)發(fā)現(xiàn)方法不僅能有效揭示網(wǎng)絡(luò)的社區(qū)結(jié)構(gòu),而且劃分結(jié)果穩(wěn)定[15].
基于局部擴展優(yōu)化的社區(qū)發(fā)現(xiàn)方法分為種子節(jié)點選取和局部社區(qū)擴展兩個階段.在種子節(jié)點選取階段,可根據(jù)隨機策略[16]、節(jié)點排名[17,18]以及極大團[8,9]等選擇出種子節(jié)點.然而如果種子節(jié)點選擇不當,則會造成社區(qū)劃分不合理的后果.為了應(yīng)對這一問題,文獻[19-24]提出構(gòu)建種子社區(qū)并從種子社區(qū)開始社區(qū)擴展的方法.在社區(qū)擴展過程中,現(xiàn)有的方法往往根據(jù)某個優(yōu)化函數(shù)融合鄰居節(jié)點.常見的優(yōu)化函數(shù)有模糊關(guān)系函數(shù)[13]、相關(guān)度函數(shù)[25]、中心度函數(shù)[26]、模塊度函數(shù)[27]、適應(yīng)度函數(shù)[18]等.然而,比起不同社區(qū)中的節(jié)點,同一社區(qū)內(nèi)的節(jié)點之間的相似程度更高.上述方法在構(gòu)建種子社區(qū)和進行社區(qū)擴展的過程中并沒同時考慮節(jié)點間連接的緊密程度和相似程度,不可避免的會存在社區(qū)劃分合理性問題.此外,在社區(qū)擴展過程中,現(xiàn)有方法往往采用貪婪的策略,逐步融合最優(yōu)的鄰居節(jié)點,制約了算法的收斂速度.
針對基于局部擴展優(yōu)化的社區(qū)發(fā)現(xiàn)方法在社區(qū)劃分結(jié)果合理性和收斂速度方面存在的問題,本文提出了一種均衡的局部社區(qū)發(fā)現(xiàn)算法,均衡考慮節(jié)點間的相似程度和連接的緊密程度進行社區(qū)擴展.該算法在選定種子節(jié)點的基礎(chǔ)上,結(jié)合相似程度和連接的緊密程度構(gòu)建種子社區(qū),以種子社區(qū)作為初始社區(qū)以迭代的方式對它進行擴展,直至收斂.本文的主要貢獻有以下幾點:
1)本文提出了一種種子社區(qū)構(gòu)建算法,該算法根據(jù)種子節(jié)點及其連通節(jié)點之間的相似程度和連接緊密程度構(gòu)建種子社區(qū),保證了種子社區(qū)的質(zhì)量,提升了社區(qū)劃分的合理性.
2)本文提出了一種兩級節(jié)點篩選機制,該機制均衡考慮相似程度和連接緊密程度篩選最適宜與社區(qū)合并的節(jié)點,緩解了因合并不恰當節(jié)點造成的社區(qū)劃分不合理問題.
3)本文提出了一種寬容的節(jié)點合并策略,可以在一次迭代中將多個節(jié)點合并到社區(qū),提高了社區(qū)擴展過程的收斂速度.
1 問題分析
在本文中,復(fù)雜網(wǎng)絡(luò)用無向無權(quán)圖G=(V,E)來表示.V為節(jié)點集合,且V={vi|i=1,2,…,n},n為節(jié)點總數(shù);E為邊集合,且E={(vi,vj)|vi∈V,vj∈Vandi≠j}.
基于局部擴展優(yōu)化的社區(qū)發(fā)現(xiàn)方法首先按照一定的策略選擇種子節(jié)點,然后從種子節(jié)點出發(fā),根據(jù)預(yù)先定義的優(yōu)化函數(shù)以迭代的方式融合鄰居節(jié)點,直至收斂,形成社區(qū).然而,如果種子節(jié)點選擇不當,將會降低社區(qū)劃分結(jié)果的合理性.針對這一問題,有學(xué)者提出在種子節(jié)點的基礎(chǔ)上構(gòu)建種子社區(qū),從種子社區(qū)出發(fā)進行社區(qū)擴展.而社區(qū)具有社區(qū)內(nèi)部的節(jié)點連接緊密,而社區(qū)之間的節(jié)點連接相對稀疏的特點.比起不同社區(qū)中的節(jié)點,同一社區(qū)內(nèi)的節(jié)點更加相似.現(xiàn)有的方法在構(gòu)建種子社區(qū)以及社區(qū)擴展過程中并沒有從社區(qū)的角度出發(fā),同時考慮社區(qū)內(nèi)部節(jié)點連接的緊密性和節(jié)點間的相似性,因而不可避免的會出現(xiàn)社區(qū)劃分結(jié)果不合理的問題.
此處,以社區(qū)擴展過程為例說明在只考慮社區(qū)內(nèi)部節(jié)點連接的緊密程度或者節(jié)點間的相似程度單個因素的情況下社區(qū)劃分結(jié)果的不合理問題.在只考慮社區(qū)內(nèi)部節(jié)點間相似程度的情況下,社區(qū)的劃分結(jié)果如圖1(a)所示.在這個劃分結(jié)果中,盡管v0和vs與v1,v2,v3,v4連接緊密,但是卻被劃分到不同的社區(qū).在只考慮社區(qū)內(nèi)部節(jié)點間連接緊密程度的情況下,社區(qū)的劃分結(jié)果如圖1(b)所示.盡管v6與v7,v8,v9,v10,v11連接緊密,但是卻被劃分到不同的社區(qū).上述這兩種劃分結(jié)果顯然是不合理的.
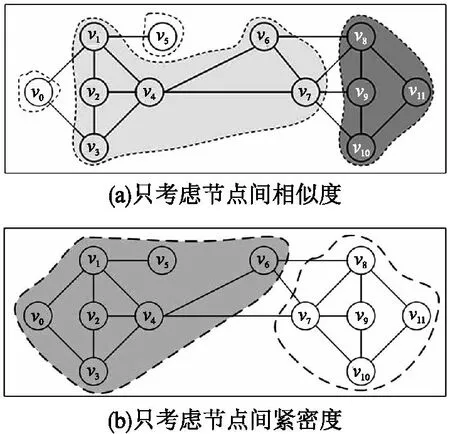
圖1 社區(qū)劃分分析Fig.1 Analysis of the community division
貪婪擴展是最常用的一種社區(qū)擴展方法,它以迭代的方式將優(yōu)化函數(shù)最優(yōu)值對應(yīng)的節(jié)點并入當前社區(qū).假設(shè)優(yōu)化函數(shù)最優(yōu)值對應(yīng)的節(jié)點只有一個,以圖2(a)所示的網(wǎng)絡(luò)為例,則要經(jīng)過5輪迭代社區(qū)擴展過程才能收斂.以圖2(b)所示,如果在每輪迭代中可以合并多個節(jié)點,則經(jīng)過2輪即可收斂.顯然,每次只合并優(yōu)化函數(shù)最優(yōu)值對應(yīng)的節(jié)點會制約社區(qū)擴展過程的收斂速度.

圖2 迭代次數(shù)分析(Ci表示第i輪迭代生成的社區(qū))Fig.2 Analysis of iterations( Ci represents the community generated by i round iteration)
2 均衡相似程度和緊密程度的局部社區(qū)發(fā)現(xiàn)算法
針對基于局部擴展優(yōu)化的社區(qū)發(fā)現(xiàn)方法在社區(qū)劃分結(jié)果合理性和收斂速度方面存在的問題,本文提出了一種新的局部社區(qū)發(fā)現(xiàn)算法,通過均衡考慮節(jié)點間的相似程度和連接的緊密程度進行社區(qū)擴展.該算法在選定種子節(jié)點后,首先結(jié)合相似程度和連接的緊密程度構(gòu)建種子社區(qū),然后以種子社區(qū)作為初始社區(qū)以迭代的方式進行擴展,直至收斂.在擴展過程中,提出了節(jié)點的兩級篩選機制,利用該機制將在相似程度和連接緊密程度兩方面優(yōu)勢均衡的節(jié)點作為最佳的節(jié)點,合并到當前社區(qū),以提高社區(qū)劃分結(jié)果的合理性.兩級篩選機制允許在一次迭代過程中合并多個節(jié)點,以提高社區(qū)擴展的收斂速度.
2.1 種子社區(qū)生成
本文方法擬通過同時考慮節(jié)點間的相似程度和連接的緊密程度構(gòu)建種子社區(qū),來消除由種子節(jié)點選擇不當引起的社區(qū)劃分結(jié)果不合理問題.在構(gòu)建種子社區(qū)時,首先要計算種子節(jié)點與其連通節(jié)點的相似程度和連接的緊密程度.根據(jù)“物以類聚,人以群分”的道理,本文從鄰居節(jié)點的角度衡量某個節(jié)點與種子節(jié)點間的相似程度.具體來講,本文認為兩個節(jié)點擁有的共同鄰居越多,這兩個節(jié)點越相似,反之亦然.基于此,本文引入了式(1)計算節(jié)點的相似程度.在該式中,v表示種子節(jié)點,v1表示v的某個連通節(jié)點,ds(vi,v)表示vi和v的相似程度,N(vi)和N(v)分別表示vi和v的鄰居節(jié)點集合.
(1)
種子社區(qū)的構(gòu)建過程就是種子節(jié)點不斷地與其連通節(jié)點合并的過程.在種子節(jié)點和某個節(jié)點合并后,種子節(jié)點和已合并節(jié)點就構(gòu)成了一個整體.在后續(xù)節(jié)點的合并過程中,只考慮和種子節(jié)點的相似程度是不合理的,應(yīng)當考慮和這個整體的相似程度.為便于計算和這個整體的相似程度,引入了超級節(jié)點來描述這個整體.
定義1.超級節(jié)點:種子節(jié)點和某個或者某些節(jié)點合并后,由這些節(jié)點和這些節(jié)點間的連邊構(gòu)成的子圖稱為種子社區(qū)構(gòu)建過程中的超級節(jié)點.
引入超級節(jié)點后,從超級節(jié)點外部連接到超級節(jié)點內(nèi)部某個節(jié)點的邊,最后要變換為連接到超級節(jié)點的邊.某個節(jié)點和超級節(jié)點間的相似程度仍然可以用式(1)計算,只需要用超級節(jié)點替換公式中的種子節(jié)點,用超級節(jié)點的鄰居節(jié)點集合替代公式中種子節(jié)點的鄰居節(jié)點集合.對于超級節(jié)點包含的各個節(jié)點,其鄰居節(jié)點有可能在超級節(jié)點內(nèi)部,也有可能在超級節(jié)點外部.超級節(jié)點的鄰居節(jié)點集合由在超級節(jié)點外部的這些鄰居節(jié)點構(gòu)成.
在構(gòu)建種子社區(qū)的過程中,除了考慮相似程度,還應(yīng)當考慮緊密程度.本文認為,節(jié)點間的連邊越多,它們之間的連接越緊密.故而,從節(jié)點間的連邊入手衡量節(jié)點間的連接緊密程度.給定節(jié)點v′,?vi∈V,且v′≠vi,記dc(vi,v′)表示v1和v′之間連接的緊密程度,由式(2)計算.在該式中,V′表示超級節(jié)點中各節(jié)點構(gòu)成的集合.
(2)
為了能同時根據(jù)節(jié)點間的相似程度和連接的緊密程度構(gòu)建種子社區(qū),引入了J因子,從相似程度和連接的緊密程度兩個角度度量某個節(jié)點適宜加入種子社區(qū)的程度,也就是適宜與種子節(jié)點或者超級節(jié)點合并的程度.?vi∈V,vi與種子節(jié)點或超級節(jié)點v′的J因子根據(jù)式(3)計算.J因子越大,越適宜與種子節(jié)點或者超級節(jié)點合并.
J(vi,v′)=dc(vi,v′)·ds(vi,v′)
(3)
在構(gòu)建種子社區(qū)時,只根據(jù)J因子決定是否將一個節(jié)點與種子合并.根據(jù)影響力傳播的三度分割原理,在所有的連通節(jié)點中,一個節(jié)點和它三跳范圍內(nèi)連通的節(jié)點關(guān)系更為密切.基于此,本文方法只考慮與種子節(jié)點的距離不超過三跳的連通節(jié)點.在構(gòu)建種子社區(qū)的具體過程中,按照與種子節(jié)點的距離依次遍歷這些連通節(jié)點.在第1輪遍歷中,只訪問與種子節(jié)點距離為一跳的各連通節(jié)點,分別計算各連通節(jié)點與種子節(jié)點的J因子,將最大J因子對應(yīng)的節(jié)點與種子節(jié)點合并,形成超級節(jié)點.在第2輪和第3輪遍歷中,分別訪問與種子節(jié)點距離為二跳和三跳的各連通節(jié)點,分別計算這些連通節(jié)點與對應(yīng)超級節(jié)點的J因子,將J因子最大的節(jié)點與超級節(jié)點合并.
超級節(jié)點最終演變?yōu)榉N子社區(qū).超級節(jié)點形成后,可能會出現(xiàn)某個連通節(jié)點與超級節(jié)點的因子大于該節(jié)點與種子節(jié)點的J因子.鑒于這一情況,在第2輪和第3輪遍歷中應(yīng)考慮超級節(jié)點的鄰居節(jié)點,即與超級節(jié)點有直接連邊的節(jié)點.綜上,本文方法構(gòu)建種子社區(qū)的過程如算法1所述.
算法1.種子社區(qū)構(gòu)建
輸入:網(wǎng)絡(luò)G=(V,E),種子節(jié)點seed
輸出:種子社區(qū)Cseeds
1.Vseeds={seed}
2.h←1,Δ←3
3.whileh≤Δ
4.rnodes←與種子節(jié)點距離為h的連通節(jié)點;
5.If(h==1)
6.計算rnodes中各節(jié)點與seed的J因子
7.最大J因子對應(yīng)的節(jié)點與種子節(jié)點合并生成超級節(jié)點
8.else
9.neinodes←獲取當前超級節(jié)點的鄰居節(jié)點
10.將僅在neinodes中出現(xiàn)的節(jié)點加入rnodes
11.計算rnodes中各節(jié)點與當前超級節(jié)點的J因子
12.將最大J因子對應(yīng)的節(jié)點加入超級節(jié)點
13.end if
14.End while
15.ReturnCseeds
2.2 第1級節(jié)點篩選
為了在社區(qū)擴展過程中同時考慮節(jié)點與社區(qū)間的相似程度和連接的緊密程度,本文根據(jù)前文定義的因子逐步合并鄰居節(jié)點直至收斂.如果一個節(jié)點是社區(qū)內(nèi)部的節(jié)點,它的所有鄰居節(jié)點都在社區(qū)內(nèi)部.如果是社區(qū)的邊界節(jié)點,它的一部分鄰居節(jié)點在社區(qū)內(nèi)部,另一部分鄰居節(jié)點則在其它社區(qū).在進行社區(qū)擴展時,應(yīng)盡量避免合并可能是邊界的節(jié)點.因此,在進行社區(qū)擴展時沒有必要去嘗試合并每個鄰居節(jié)點.基于此,本文引入了對節(jié)點的第1級篩選.
第1級篩選的目標是將大概率不屬于給定社區(qū)的節(jié)點排除在給定社區(qū)可能合并的節(jié)點范圍之外.為了達到這一目的,引入了歸屬度,利用歸屬度來判斷某個鄰居節(jié)點屬于給定社區(qū)的概率.?vi∈V,vi相對于給定社區(qū)的歸屬度記為db(vi,C),根據(jù)式(4)計算.在該式中,Vc表示社區(qū)C的節(jié)點集合.當db(vi,C)的值大于等于給定閾值θb時,認為vi可能屬于社區(qū)C;否則,認為vi不可能屬于社區(qū)C.
(4)
Vmerge(C)={vi|vi∈N(C) anddb(vi,C)≥θb}
(5)
在節(jié)點歸屬度的基礎(chǔ)上,引入了可合并節(jié)點集合.在迭代擴展過程中,社區(qū)只能融合可合并節(jié)點集合中的節(jié)點.記給定社區(qū)C的可合并節(jié)點集合為Vmerge(C),由式(5)表示.在該式中,N(C)為社區(qū)C的鄰居節(jié)點集合.由式(5)中的條件db(vi,C)≥θb可知,不可能屬于社區(qū)C的節(jié)點被排除在可合并節(jié)點集合之外,從而實現(xiàn)了第1級篩選的目標.算法2展示了可合并節(jié)點集合的構(gòu)建過程.
算法2.可合并節(jié)點集合
輸入:網(wǎng)絡(luò)G=(V,E),當前正在擴展社區(qū)C,閾值θb
輸出:可合并節(jié)點集合Vmerge
1.Vmerge=?
2.neinodes←C的鄰居節(jié)點
3.for eachnodeinneinodes
4.計算db(node,C)
5.ifdb(vi,C)≥θb
6.Vmetge=Vmerge∪{node}
7.end if
8.end for
9.ReturnVmetge
2.3 第2級節(jié)點篩選
為了能根據(jù)節(jié)點間的相似程度和連接的緊密程度劃分社區(qū),本文方法在社區(qū)擴展過程中仍根據(jù)J因子來選擇可以合并的節(jié)點.在社區(qū)擴展過程中,J因子由節(jié)點和社區(qū)的相似程度以及節(jié)點與社區(qū)連接的緊密程度共同決定.?vi∈V,vcur表示正在擴展的社區(qū)Ccur對應(yīng)的超級節(jié)點.在ds(vi,vcur)較小,也就是vj與當前擴展社區(qū)相似度較低的情況下,如果dc(vj,ccur)足夠大,也就是vj與當前社區(qū)連接的緊密程度足夠大,那么J(vj,ccur)也較大,從而使得vj與當前擴展社區(qū)合并.在dc(vj,vcur)較小的情況下,如果ds(vj,vcur)足夠大,也會使得vj與當前社區(qū)擴展社區(qū)合并.前一種情況相當于在社區(qū)合并過程中過于強調(diào)緊密度,后一種情況則相當于過于強調(diào)相似度.
這兩種情況都與本文均衡考慮相似程度和連接緊密程度的初衷相悖.基于此,本文提出了第2級節(jié)點篩選.第2級節(jié)點篩選的目標是從可合并節(jié)點集合中篩選出上述兩種情況涉及到的節(jié)點,將它們從可合并節(jié)點集合中刪除,并從可合并節(jié)點集合中選擇相似程度和連接緊密程度都能兼顧的節(jié)點,也就是相似程度和連接緊密程度均衡的節(jié)點,合并到當前社區(qū).基于此,本文引入了以下均衡性判定策略:
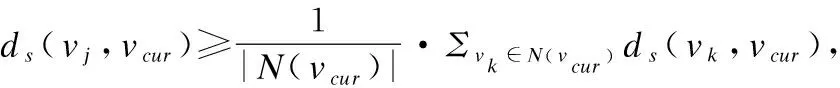
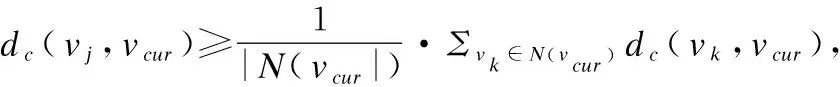
按照均衡性判定策略1-2對Vmerge(C)的節(jié)點進行篩選后,Vmerge(C)中保留的節(jié)點就是相似程度和連接緊密程度均衡的節(jié)點.為了提高社區(qū)擴展過程的收斂速度,本文引入了如下的合并策略.該策略通過允許在一輪迭代中合并滿足條件的多個節(jié)點,來提升合并過程的收斂速度.
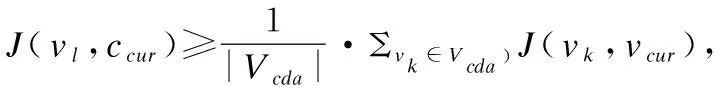
通過執(zhí)行均衡性判定策略1-2可以保證將相似程度和連接緊密程度都比較高的節(jié)點合并到當前擴展社區(qū),可以實現(xiàn)第2級篩選的目標.貪婪策略在每輪迭代擴展過程中只合并優(yōu)化函數(shù)最大值對應(yīng)的節(jié)點,限制了算法的收斂速度.與貪婪策略不同,本文提出的合并策略在每輪迭代過程中將滿足合并條件的多個節(jié)點都合并到當前社區(qū)中,以此來加快社區(qū)擴展過程的收斂速度.根據(jù)上述策略,本文方法擴展社區(qū)的過程如算法3所示.
算法3.社區(qū)擴展
輸入:網(wǎng)絡(luò)G=(V,E),種子節(jié)點Seed
輸出:局部社區(qū)Ccur
1.Ccur←Cseeds
2.Vcda←為Ccur創(chuàng)建可合并節(jié)點集合
3.Jsum=0
4.WhileVcda≠?
5.dcresults←計算Vcda中每個節(jié)點與Ccur的緊密度
6.dsresults←計算Vcda中每個節(jié)點與Ccur的相似度
7.dsave←計算平均相似程度
8.dsave←計算平均緊密程度
9.for eachnodainVcda
10.Ifds(node,vcur) 11.從Vcda中刪除node 12.else 13.計算node與ccur的J因子 14.Jsum←node與Ccur的J因子+Jsum 15.End if 16. End for 17. IfVcda!=? 18.Jave←計算Vcda節(jié)點與Ccur的J因子平均值 19.else 20. break 21. for eachnodeinVcda 22.ifJ(node,vcur)≥Jave 23.將node合并到Ccur 24.End if 25. End for 26.Vcda←為Ccur創(chuàng)建可合并節(jié)點集合 27.End while 28.ReturnCcur 假設(shè)網(wǎng)絡(luò)中節(jié)點的平均度為d,算法迭代t次檢測完整社區(qū).本文算法主要分為種子社區(qū)生成和種子社區(qū)擴展兩個階段.在種子社區(qū)生成階段,假設(shè)超級節(jié)點的鄰接節(jié)點在種子節(jié)點三跳之內(nèi)的節(jié)點個數(shù)為q,當h為1時計算給定種子節(jié)點與鄰接節(jié)點的J因子值的時間復(fù)雜度為O(d);當h不為1時計算超級節(jié)點和其符合條件鄰居節(jié)點的J因子值的時間復(fù)雜度為O(q).因此,種子社區(qū)生成的時間復(fù)雜度為O(d+q).在種子社區(qū)擴展階段,引入節(jié)點兩級節(jié)點篩選機制.在第1級種子節(jié)點篩選,根據(jù)歸屬度篩選社區(qū)的鄰居節(jié)點,假設(shè)社區(qū)的平均鄰接節(jié)點個數(shù)為m,則第1級節(jié)點篩選的時間復(fù)雜度為O(m);假設(shè)經(jīng)過第1級節(jié)點篩選,可合并節(jié)點集合中的節(jié)點個數(shù)為k,則在第2級節(jié)點篩選階段中,計算可合并節(jié)點集合中各個節(jié)點與當前計算社區(qū)相似程度和連接緊密程度的時間復(fù)雜度都為O(k),按照均衡判定策略篩選遍歷各個節(jié)點的時間復(fù)雜度為O(k).假設(shè)按照均衡判定策略篩選后可合并節(jié)點集合的節(jié)點個數(shù)為n,按合并策略遍歷該集合中節(jié)點的時間復(fù)雜度為O(n),篩選滿足融合社區(qū)節(jié)點的時間復(fù)雜度為O(n).由于滿足合并策略的節(jié)點屬于可合并候選集k≥n,即,則第2級種子節(jié)點篩選的時間復(fù)雜度為O(k).因此,種子社區(qū)擴展階段的時間復(fù)雜度為O(m+k).綜上所述,本文算法的時間復(fù)雜度約為O(t(d+q+k+m)). 為了驗證本文算法的正確性和有效性,在多個真實數(shù)據(jù)集和人工數(shù)據(jù)集上與LCDMD算法[16]、LCDFSR算法[28]、MULTICOM算法[29]、MLC算法[30]進行了對比實驗.實驗中用到的操作系統(tǒng)為行Win10,處理器為Intel(R)Pentium(R)CPU G4600 @ 3.60GHz,內(nèi)存容量為16GB.所有算法由python語言實現(xiàn). 在實驗過程中選取了6個真實數(shù)據(jù)集和9個人工數(shù)據(jù)集,這些數(shù)據(jù)集的社區(qū)結(jié)構(gòu)都是已知的. 1)真實數(shù)據(jù)集 Karate網(wǎng)絡(luò)[31]是根據(jù)一個空手道俱樂部成員間的關(guān)系創(chuàng)建的社交網(wǎng)絡(luò),包含34個節(jié)點和78條邊,共分成2個社區(qū).Dolphins網(wǎng)絡(luò)[32]由海豚之間交互行為構(gòu)成的社交網(wǎng)絡(luò),包含62個節(jié)點和159條邊,共分成2個社區(qū);Polbooks網(wǎng)絡(luò)[33]是根據(jù)美國政治書籍網(wǎng)絡(luò),包含105個節(jié)點和441條邊,共分成3個社區(qū);Football網(wǎng)絡(luò)[34]是根據(jù)足球比賽構(gòu)建的網(wǎng)絡(luò),包含115個節(jié)點和616條邊,共分成12個社區(qū);DBLP網(wǎng)絡(luò)[35]是一個科學(xué)家合作網(wǎng)絡(luò),該網(wǎng)絡(luò)包含317080個節(jié)點和1049866條邊,共分成13477個社區(qū);亞馬遜網(wǎng)絡(luò)[35]是一個關(guān)于在亞馬遜網(wǎng)站上銷售產(chǎn)品的網(wǎng)絡(luò),該網(wǎng)絡(luò)有334863個節(jié)點和925872條邊,共分成75149個社區(qū). 2)人工數(shù)據(jù)集 人工數(shù)據(jù)集根據(jù)Lancichinetti等人[36]提出的LFR基準網(wǎng)絡(luò)生成.在生成過程中,參數(shù)配置如下:N=10000,k=17,maxk=3,minc=20,maxc=70,μ從0.1開始取值,每次遞增0.05,直到μ=0.5,共生成9個人工網(wǎng)絡(luò).μ值越大,給對應(yīng)網(wǎng)絡(luò)劃分社區(qū)的難度越大.故而,在實驗中μ的最大值只取到0.5. 由于Karate、Dolphins、Polbooks、Football和人工網(wǎng)絡(luò)數(shù)據(jù)集中包含的節(jié)點數(shù)較少,在實驗過程中將這些數(shù)據(jù)集中的每一個節(jié)點都視作種子節(jié)點,分別從各個種子節(jié)點出發(fā)進行社區(qū)劃分.而DBLP和Amazon數(shù)據(jù)集中包含的節(jié)點數(shù)較多,在實驗過程中隨機從每個數(shù)據(jù)集中選取10000個不同的節(jié)點作為種子節(jié)點,分別從每個種子出發(fā)進行社區(qū)劃分. 本文采用調(diào)和均值F-Score[15]作為評價指標,來評估本文方法的正確性和有效性,這個指標根據(jù)式(6)計算.在式(6)中,Precision是查準率,表示被正確劃分的節(jié)點占所有實際劃分節(jié)點的比例;Recall是查全率,表示被正確劃分的節(jié)點占真實劃分節(jié)點的比例.Precision和Recall分別根據(jù)式(7)和式(8)來計算.在式(7)和式(8)中,CT表示由種子節(jié)點所屬真實社區(qū)中節(jié)點構(gòu)成的集合,CF表示由算法檢測出的種子節(jié)點所屬社區(qū)節(jié)點構(gòu)成的集合. (6) (7) (8) 本文方法在第1級節(jié)點篩選過程中需要計算各鄰居節(jié)點相對于給定社區(qū)的歸屬度,根據(jù)計算結(jié)果和預(yù)設(shè)的閾值θb把大概率不屬于給定社區(qū)的鄰接節(jié)點排除在外.本文通過實驗的方法設(shè)置θb的取值.令θb從0.1開始取值,每次遞增0.1,共取9個不同的值.分別在θb取不同值時,對各個數(shù)據(jù)集進行社區(qū)劃分,并根據(jù)劃分結(jié)果計算θb取不同值時算法在不同數(shù)據(jù)集上的F-Score平均值,結(jié)果如圖3和圖4所示.綜合考慮各個數(shù)據(jù)集上的結(jié)果,在本次實驗中θb的值設(shè)置為0.4. 圖3 θb取不同值時本文方法在真實數(shù)據(jù)集上的結(jié)果Fig.3 Experimental results with different values of θb on the real datasets 圖4 θb取不同值時本文方法在人工數(shù)據(jù)集上的結(jié)果Fig.4 Experimental results with different values of θb on the artificial datasets 圖5展示了各算法在真實數(shù)據(jù)集上的對比結(jié)果.圖5(a)展示的是各算法Precision指標平均值的對比結(jié)果.由此圖可知,本文算法在Karate、Polbooks、Football和Amazon數(shù)據(jù)集上的Precision指標平均值在所有算法中是最高的,在Dolphins和DBLP數(shù)據(jù)集上的Precision指標平均值僅分別高于LCDFSR算法和MLC算法. 圖5 在真實數(shù)據(jù)集上的實驗結(jié)果Fig.5 Experimental results on the real datasets 圖5(b)展示的是各算法Recall指標平均值的對比結(jié)果.由此圖可知,本文算法在Dolphins、DBLP和Amazon數(shù)據(jù)集上的Recall指標平均值在所有算法中是最高的,在Polbooks數(shù)據(jù)集上的Recall指標平均值僅次于LCDFSR算法,在Karate數(shù)據(jù)集上的Recall指標平均值高于LCDMD算法和MULTICOM算法,在Football數(shù)據(jù)集上的Recall指標平均值高于LCDMD算法和MLC算法. 表1展示了各算法在真實數(shù)據(jù)集上F-Score指標的平均值,最高的F-Score值用粗體顯示,次高的F-Score值加下劃線顯示.由此表可知,本文算法的F-Score指標平均值均高于4種對比算法.在從Karate到Amazon的6個數(shù)據(jù)集上,本文算法的F-Score值相比于次高的F-Score值分別提高了2.13%、3.42%、6.86%、2.12%、3.35%以及7.94%. 表1 算法在真實數(shù)據(jù)集上的F-Score指標對比結(jié)果Table 1 F-Score metrics comparison results of algorithm on real datasets 圖6展示各算法在真實數(shù)據(jù)集上的運行時間.由圖可知,本文算法的運行時間明顯低于各對比算法.由于DBLP數(shù)據(jù)集和Amazon數(shù)據(jù)集規(guī)模較大,各算法在這兩個數(shù)據(jù)集上的運行時間遠大于在其它4個數(shù)據(jù)集上的運行時間.考慮到篇幅和圖形的美觀,設(shè)置了斷層. 圖6 不同算法在真實數(shù)據(jù)集上的運行時間Fig.6 Running time of different algorithms on real datasets 圖7展示了各算法在人工數(shù)據(jù)集上的對比結(jié)果.圖7(a)展示的是各算法Precision指標平均值的對比結(jié)果.由此圖可知,本文算法和LCDFSR算法的Precision指標平均值要高于其它3個對比算法.在μ值分別為0.25、0.4和0.5時,本文算法的Precision指標平均值略低于LCDFSR算法;在μ取其它6個值的情況下,本文算法的Precision指標平均值與LCDFSR算法持平. 圖7 在人工數(shù)據(jù)集上的實驗結(jié)果Fig.7 Experimental results on the artificial datasets 圖7(b)展示的是各算法Recall指標平均值的對比結(jié)果.由此圖可知,本文算法的Recall指標平均值僅在μ值分別為0.45和0.5兩種情況下略低于MULTICOM算法;在μ取其它7個值的情況下,本文算法的Recall指標平均值均高于所有對比算法. 表2展示了各算法在人工數(shù)據(jù)集上F-Score指標的平均值,最高的F-Score值用粗體顯示,次高F-Score值加下劃線顯示.由此表可知,本文算法的F-Score指標平均值均高于4種對比算法.在4個對比算法中,LCDMD算法在值分別為0.4、0.45和0.5時相對于其他3個算法表現(xiàn)最好,在取其他6個值時,LCDFSR算法相對于其他3個算法表現(xiàn)最好.本文算法在取前6個值時的F-Score指標平均值相對于LCDFSR算法分別提高了0.77%、3.07%、6.67%、7.90%、8.71%和20.37%,在取后3個值時的F-Score指標平均值相對于LCDMD算法分別提高了21.51%、19.47%和20.70%.圖8展示了各算法在人工數(shù)據(jù)集上的運行時間.由圖可知,與LCDMD算法、MULTICOM算法和MLC算法相比,本文算法的運行時間更短.與LCDFSR算法相比,本文算法的運行時間則略長.但考慮到本文算法的F-Score值要明顯高于LCDFSR算法,而且在值增大的過程中,LCDFSR算法的F-Score值下降劇烈,而本文算法則表現(xiàn)較為平穩(wěn),故認為本文算法更優(yōu). 表2 算法在人工數(shù)據(jù)集上的F-Score指標對比結(jié)果Table 2 F-Score metrics comparison results of algorithm on artificial datasets 圖8 不同算法在人工數(shù)據(jù)集上的運行時間Fig.8 Running time of different algorithms on artificial datasets 本文提出了一種局部社區(qū)劃分方法.該方法將局部社區(qū)劃分分為種子社區(qū)構(gòu)建和種子社區(qū)擴展兩個階段.在種子社區(qū)構(gòu)建階段,根據(jù)節(jié)點間的相似程度和連接緊密程度生成種子社區(qū).在種子社區(qū)擴展階段,引入節(jié)點的兩級篩選機制,利用該機制將在相似程度和連接緊密程度兩方面優(yōu)勢均衡的節(jié)點作為最佳的節(jié)點,合并到當前社區(qū),以提高社區(qū)劃分結(jié)果的合理性.兩級篩選機制允許在一次迭代過程中合并多個節(jié)點,以提高社區(qū)擴展過程的收斂速度.在多個真實數(shù)據(jù)集和多個人工數(shù)據(jù)集上的對比實驗證明了本文方法的正確性和有效性.2.4 算法復(fù)雜度分析
3 實 驗
3.1 實驗數(shù)據(jù)
3.2 評價指標
3.3 實驗參數(shù)
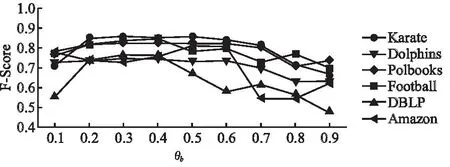

3.4 真實數(shù)據(jù)集上的對比實驗與分析
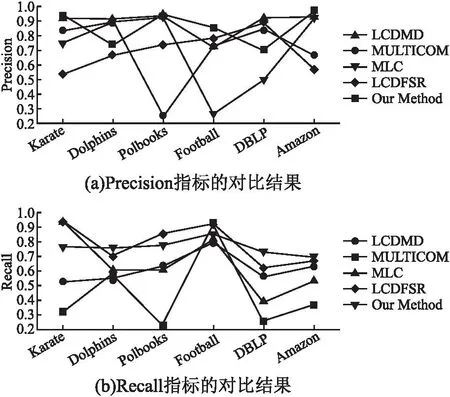
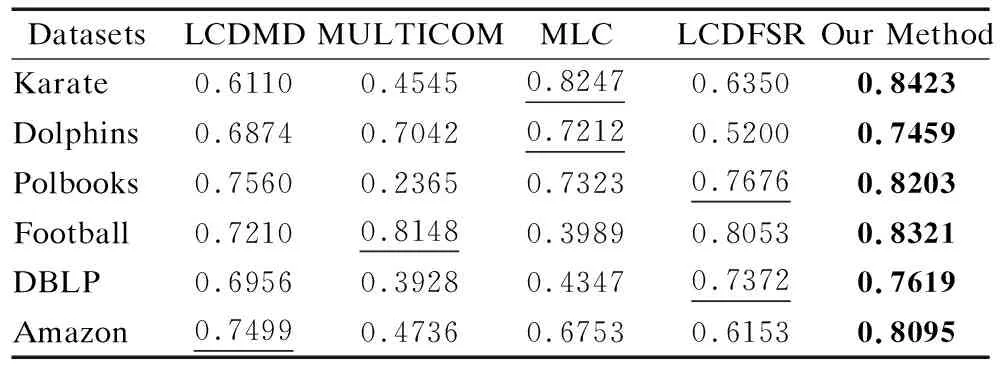
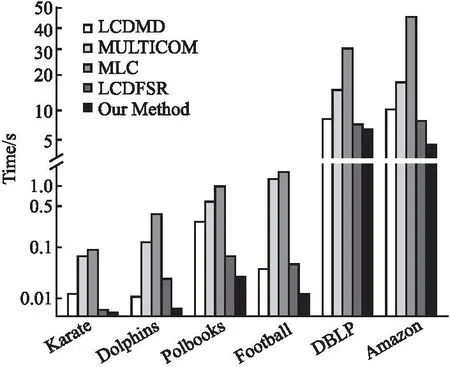
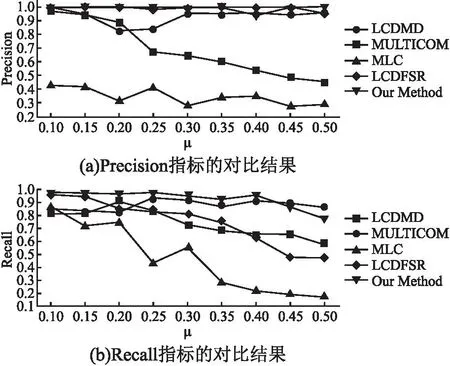
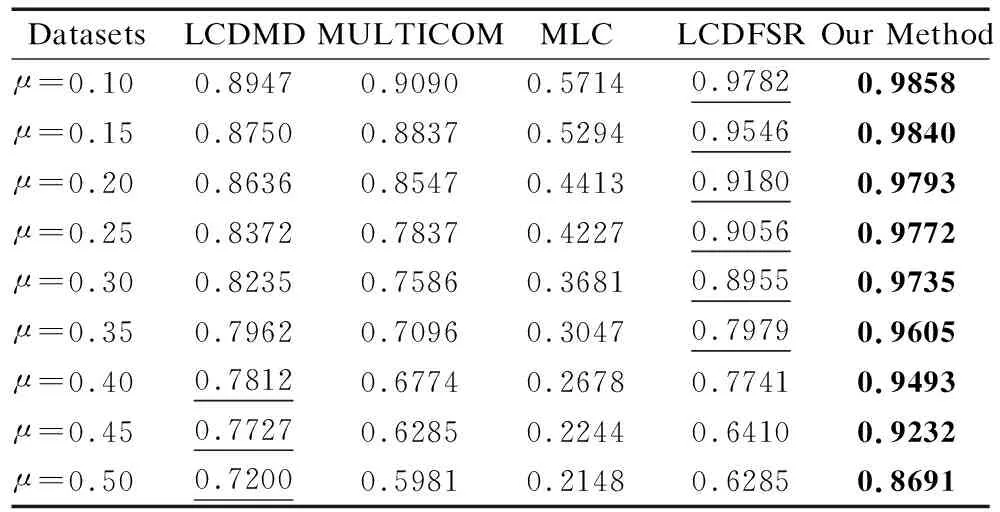
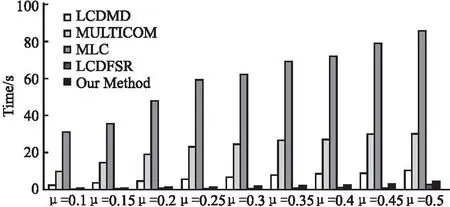
3.5 人工數(shù)據(jù)集上的對比實驗與分析
4 結(jié)束語

