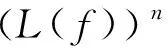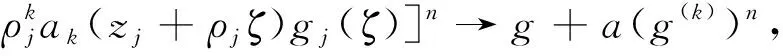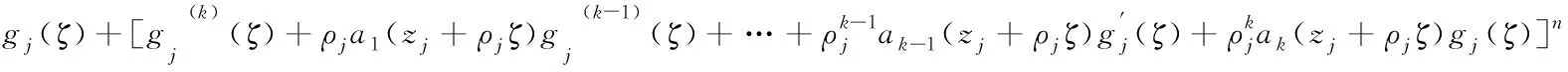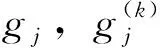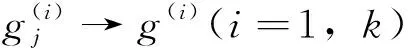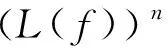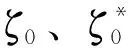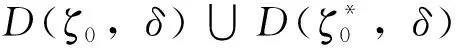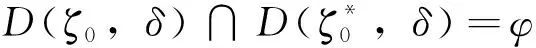關于f+a(L(f))n的正規定則
冉 娜,楊 祺
(新疆師范大學 數學科學學院,新疆 烏魯木齊 830017)
0 引言
D是復數域內的一鄰域,F為區域D內的一亞純函數族,{fn}為函數列,{fnv}為函數列{fn}的子序列,若?{fn}?F,均?{fnv}在區域D內按球距內閉一致收斂到一個亞純函數或者∞,則稱F在區域D內是正規的[1-3]。
用σ(x,y)表示x和y的球面距離[4]。2013年,雷春林等在文獻[5]中證明了定理A。
定理A設F為區域D內的一亞純函數族,a≠0,b為兩個有窮復數,n≥2,k為兩個正整數,若對于定義在D內的?f∈F,f的零點重級至少是k+1,且滿足
f+a(f(k))n≠b,
(1)
則F在區域D上正規。
2021年,曾翠萍等考慮到分擔值的情形,將定理A進行了推廣,在文獻[6]中證明了定理B。
定理B設n≥2,k是兩個正整數,a≠0,b為兩個有窮復數,F為區域D上的亞純函數族,且滿足:
(1)對于?f∈F,f的零點重級至少是k+1;
(2)對于?f∈F,f(k)(z)的零值點不是f(z)的b值點;
(3)對于F內的任意兩個函數f和g,f+a(f(k))n和g+a(g(k))n分擔b,則F在區域D上正規。
基于以上的研究,文章將定理A和定理B中的f(k)換成關于f的微分多項式L(f),這里L(f)=f(k)(z)+a1f(k-1)(z)+…+akf(z),ai(z),i=1,2,…,k,是區域D上的全純函數,得到了兩個新的有關微分多項式的正規定則。
1 一些引理
引理1[7]單位圓Δ內,設F是該區域內的一族亞純函數,?f∈F的零點重級均≥k。若F在Δ內不正規,則對0≤α≤k,存在
(1)一個數0 (2)一個點列:|zj| (3)一個函數列fj∈F, (4)一個正數列ρj→0+, 引理2[8]若全純函數f的球面導數f#在上有界,則f的級至多為1。 引理3[9]若超越亞純函數f≠0,且a(≠0)為有窮復數,n≥2為正整數,則f+a(f(k))n有無窮多個零點。 引理4[10]設有理函數f≠0,a(≠0)為有窮復數,k、n為兩個正整數,滿足n≥2,則f+a(f(k))n至少存在nk+1個零點。 (2) 其中c和d為兩個不同的復常數。 定理1設F為區域D內的一亞純函數族,a≠0,b為兩個有窮復數,n、k為兩個正整數,n≥2,若對于定義在D內任意f∈F,f的零點重級至少是k+1,且滿足 (3) 則F在區域D上正規。 證明不失一般性,令D=Δ,設F為單位圓Δ內的一亞純函數族,若F在Δ內不正規,則至少存在一點z0∈Δ,使得F在z0處不正規,接下來,將分兩種情況討論。 情形1b=0 根據引理1可知,?fj∈F,zj→z0,ρj→0+使得 (4) 又根據式(4)知 (5) 故由Hurwitz定理知,g+a(g(k))n≡0,則g是一個整函數,根據引理2可知,g的級至多為1,又因為g≠0,故可令g=ecζ+d,c、d為兩個復數,c≠0,因此 ecζ+d+a(ckecζ+d)n=ecζ+d{1+acnk(ecζ+d)n-1}≡0, (6) 當n≥2時是不可能的,故而F在Δ內正規。 情形2b≠0時 根據引理1可知,?fj∈F,zj→z0,ρj→0+使得 fj(zj+ρjζ)+a[L(fj(zj+ρjζ))]n-b→a(g(k))n-b。 (7) 若a(g(k))n≠b,根據Nevanlinna第二基本定理可知 (8) 又根據式(7)知 =fj(zj+ρjζ)+a[L(fj(zj+ρjζ))]n-b→a(g(k))n-b, (9) 故g是一個k次多項式,又因為根據已知條件知g的零點重級至少k+1,故矛盾。證畢。 定理2設n、k是兩個正整數,n≥2,a、b為兩個有窮復數,a≠0,F為區域D上的亞純函數族,且滿足: (1)對于?f∈F,f的零點重級至少是k+1; (2)對于?f∈F,L(f)的零值點不是f(z)的b值點; 證明不失一般性,令D=Δ,設F為單位圓Δ內的一亞純函數族,若F在Δ內不正規,則至少存在一點z0∈Δ,使得F在z0處不正規,接下來,將分兩種情況討論。 情形1b=0 由定理條件知,對于D內?f∈F有f≠0,否則,假設f=0,f的零點重級至少是k+1,則f(i)=0,i=1,2,…,k即L(f)=0,這與條件(2)矛盾。 若想證F在區域D內正規,即證F在?z0∈D處正規。 對于D內?f∈F,則有f(z0)+a[L(f(z0))]n=0或者f(z0)+a[L(f(z0))]n≠0,故存在δ>0,使得在Dδ={ζ:|ζ-ζ0|<δ}內,f+a[L(f)]n至多有一個不同的零點,由條件(c)知,?g∈F,g+a[L(g)]n至多有一個不同的零點。 假設F在z0處不正規,根據引理1可知,?fj∈F,zj→z0,ρj→0+使得 (10) gj(ζ)+[gj(k)(ζ)+ρja1(zj+ρjζ)gj(k-1)(ζ)+ …+ 我們斷言g+a(g(k))n至多有一個不同的零點。 D(ζ0,δ)={ζ:|ζ-ζ0|<δ}, (11) (12) fj(zj+ρjζj)+a[L(fj(zj+ρjζj))]n=0, (13) (14) 又因為fj+a[L(fj)]n在Dδ={ζ:|ζ-ζ0|<δ}內至多有一個不同的零點,從而 (15) 情形2b≠0時 對于D內的?f∈F,則有f(z0)+a[L(f(z0))]n=b或者f(z0)+a[L(f(z0))]n≠b,故存在δ>0,使得在Dδ={ζ:|ζ-ζ0|<δ}內,f+a[L(f)]n-b至多有一個不同的零點,由分擔條件知,?g∈F,g+a[L(g)]n-b至多有一個不同的零點。 假設F在z0處不正規,根據引理1可知,?fj∈F,zj→z0,ρj→0+使得 fj(zj+ρjζ)+a[L(fj(zj+ρjζ))]n-b→a(g(k))n-b。 (16) 類似于情況1的討論,a(g(k))n-b至多有一個不同的零點。 由于n≥2,故wn=b/a至少存在2個不同的根,不妨設g(k)≠b1,g(k)=b2至多只有一個不同的零點,若是g超越亞純函數,利用Nevanlinna理論,可得 (17) 因此T(r,g(k))=O(logr)+S(r,g(k)),矛盾。因此g為有理函數,因為g(k)≠b1,g的零點重級至少k+1。根據引理5知 (18) 其中:c和d為兩個不同的復常數且b1≠0。因此 (19) 其中:A≠0為復常數,從而g(k)(ζ)=b2存在至少k+1不同的零點,這與g(k)(ζ)=b2至多只有一個零點矛盾。 綜上所述,F在區域D內正規。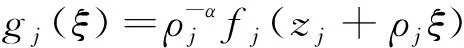
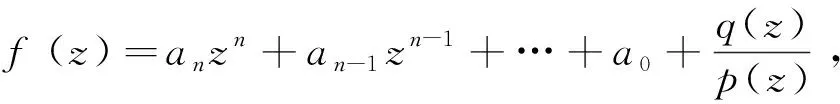
2 主要結果及定理證明