機場航站樓空調系統運行能耗優化模型
趙植竹
(山東省機場管理集團煙臺國際機場有限公司,山東煙臺 264006)
0 引言
機場航站樓空調系統用電量占航站樓總耗電量的35%~65%,其運行能耗是機場建筑能耗的主要構成部分。因為航站樓空調系統在組件選型時大多依據設計日負荷,而在實際運行過程中,很多組件長時間處于低負荷運行狀態,運行效率較低,造成大量能源浪費。因此,構建其運行能耗優化模型,對于降低機場建筑能耗、實現節能發展,具有重要現實意義。空調系統運行能耗的優化主要取決于對供冷需求與供應的精準對接,因此需要考慮以逐時供冷負荷預測值為基礎來構建模型,以精準的冷負荷預測來降低運行能耗支出,達到運行能耗優化目標。
1 機場航站樓逐時供冷負荷預測
依據功能特征與圍護結構特征,將機場航站樓供冷負荷分為圍護供冷負荷、太陽輻射供冷負荷、有組織新風供冷負荷、無組織滲風供冷負荷、人體散熱供冷負荷與機器設備散熱供冷負荷,并根據熱量傳遞的物流過程,構建機場航站樓供冷負荷預測模型:
式中 K——圍護結構的傳熱系數,W/(m2·℃)
tτ-ξ-tn——溫度波作用時刻計算溫度與室內溫度的差值,℃
F1——圍護結構幕墻面積,m2
F2——外窗幕墻面積,m2
Xg——構造修正系數
Iwτ——在沒有遮陽狀態下玻璃的太陽輻射供冷負荷,W/m2
G1——有組織新風風量,kg/s
G2——無組織滲風風量,kg/s
Hτ——室外的空氣焓值,kJ/kg
Hn——室內的空氣焓值,kJ/kg
n——室內人員數量,個
qs——人員輕度勞動狀態下的顯熱發熱量,W
ql——人員輕度勞動狀態下的潛熱發熱量,W
Wτ——所有設備設施在消耗電能時形成的發熱量總和,W
根據相關研究查,單位人員總發熱量(qs+ql)為181 W。
考慮到上述模型存在部分數據難以獲取到準確數值的問題,因此采用回歸分析法反復對實際供冷量進行測量,并根據上述模型重復計量對應時刻的預估供冷量,將上述數據作為訓練集合,以回歸模型建立二者間的回歸關系,從而獲取到較為精準的未知參數,并將集中數據代入檢驗,通過對比未來運行時刻下的實際供冷量與預估供冷量的差值大小,判斷模型的有效性。以上述方法構建的機場航站樓供冷負荷預測模型為基礎,充分利用已有數據,通過回歸分析的方式推斷出無法獲取到準確數值的未知參數,并將未知參數重新代入到模型中進行檢驗,通過實際值與預估值的對比檢驗模型,如果發現數據仍存在較大誤差,可獲取更多樣本量進行模型校正,從而實現對建筑供冷負荷的精準計算。
2 機場航站樓空調系統運行能耗優化模型構建
本文設計提出的航站樓空調系統優化模型有制冷機組、冷卻塔、蓄冰罐等組成。系統運行耗能優化模型設計中,根據不同系統組件進行了模型設計。
2.1 制冷機組能耗優化模型
制冷機組是空調系統中的關鍵能耗部分,其耗能約占整體的70%以上,因此有必要對該部件能耗進行優化設計。優化中以制冷能耗比EER 作為負荷性能先進指標,其計算方法如下:
制冷機組在不同工況條件下的部分負荷率為:
其中,EER 為制冷機組額定工況下的能效比;QCHLR為第i 時刻下機組的制冷或蓄冰量;X(j)為第j臺機組的負荷分配系數;CCAP 為機組制冷或蓄冰的最大供冷量。
機組運行過程中冷卻系統的進水溫度會直接影響冷凝溫度,而機組中冷凍水的出水溫度則會影響其蒸發溫度。航站樓空調系統多臺制冷機組在滿足基本制冷需求的前提下,通過聯合運行模式可滿足最低能耗要求,提升機組的能效比,不僅可以有效降低系統的啟停次數,還可以提高機組的運行效率。因此,確定多臺制冷機組聯合運行的能耗優化模型如下:
其約束條件為:
其中,i=1,2,…,N。
2.2 冷卻塔能耗優化模型
考慮到其運行的熱交換原理,電機驅動風扇工作后會帶走冷卻水中的熱量,從而有效降低冷凝器的出口溫度。因此,冷卻塔能耗與電機運行效率與冷凝器的熱負荷具有直接關系,冷卻塔的能耗優化設計模型為:
2.3 蓄冰罐能耗優化模型
設備運行過程中通常會在低電價時期進行蓄冰,在高電價時期進行融冰,從而達到制冷降溫的效果。該設備由直接蓄冰和間接蓄冰系統共同構成,對蓄冰罐的能耗研究主要以分析融冰性能速率為主。在航站樓空調系統蓄冰設備應用過程中,本文在分析融冰速率時引入蓄冰罐狀態變量r 和變化率u,則融冰速率:
其中,u(i)為第i 時刻的融冰率,r(i)為第i 時刻的剩余冰量。
u(i)在不同時刻的變化是唯一存在的,因此可計算確定融冰速率的最大值和最小值:
集合多項式擬合的方法,以蓄冰罐融冰時間作為自變量,第i 時刻的已融冰總量R(i)為因變量,因此可確定在i 時刻最大融冰速率下的能耗優化模型為:
2.4 最小化運行費用優化模型
航站樓空調系統運行費用由電度電費和需量電費組成,開展系統能耗優化設計應以降低系統運行費用為目標,在多類能耗設備運行下結合能耗優化模型可計算得出航站樓空調系統運行費用最小優化模型為:
其約束條件為:
其中,i=1,2,…,N,e(i)為第i 時刻電價;Psys為某時刻總用電量;QTES(i)為第i 時刻蓄冰罐供冷量。
考慮到航站樓空調系統運行問題為多目標問題,因此采用自適應權重wk將其轉換為單目標問題:
充分利用種群中有利信息進行權重的動態更新,根據目標值的最大解與最小解不斷迫近正理想點,最終求得動態的最大極限點與最小極限點,而二者的變化也將引起wk的變化:
因此,可以將最小化運行費用問題通過等價轉化為最大化問題,并將式(14)代入單目標函數表達式,得到新的目標函數為:
3 實例應用
某航站樓共有3 臺制冷機組與1 臺蓄冰罐,根據空調系統制冷與蓄冷設備運行情況,將相關數據代入模型(1)中計算得到冷負荷預測值,并選擇冷負荷的100%、75%、50%、25%四種狀態進行檢驗,所選取的狀態涵蓋了冷負荷的不同情況,從而可以確保在不同狀態下均可以確定最優運行模式。
(1)在100%冷負荷下,此時系統運行負荷最大,所有冷機均處于滿負荷運行狀態,由蓄冷設備完成剩余冷量供應,即蓄冷設備與制冷設備處于聯合運行模式,此時的優化控制結果與冷機優先一致(圖1)。

圖1 100%冷負荷下的運行優化策略
(2)在75%冷負荷下,系統運行負荷偏大,此時通過Matlab 變成求解可得到運行優化策略:冷機3 僅在負荷高峰期開啟,且3 臺冷機的優先啟動權以天為單位進行循環,可以保證冷機的總運行時間保持一致,此時所有冷機均接近滿負荷運行且處于節能狀態(圖2)。
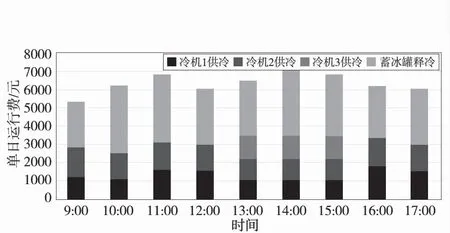
圖2 75%冷負荷下的運行優化策略
(3)在50%冷負荷下,系統運行負荷處于中間狀態,系統大部分時間處于該狀態下,此時可有效縮短機組高峰段運行時間,實現費用最小化的目標。在此狀態下,空調系統同時包含和蓄冰罐融冰模式與聯合供冷模式,且有效借助前一種模式來控制機組的運行時間(圖3)。
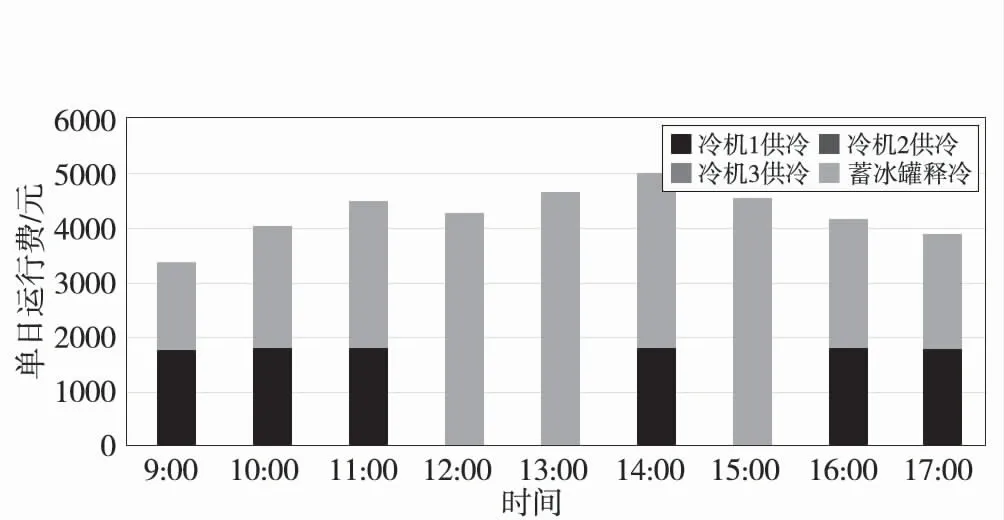
圖3 50%冷負荷下的運行優化策略
(4)在25%冷負荷下,系統運行負荷較小,此時蓄冰罐融冰模式完全可以滿足冷負荷需求,因此在夜間不需要蓄滿蓄冷罐,在白天進行釋冷,此時與蓄冰罐融冰優先一致,無需冷機運行(圖4)。
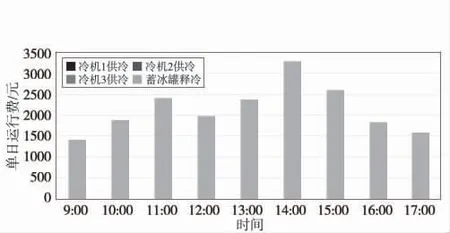
圖4 25%冷負荷下的運行優化策略
因此,在不同負荷狀態下均可以找到空調系統最優運行模式,且與傳統的冷機優先模式進行對比,75%冷負荷下單日可減少2107 元的運行費,50%冷負荷下單日可減少1399 元,25%冷負荷下單日可減少1316 元,因此在4 種負荷狀態下均滿足優化控制目標。同時,從能耗方面進行對比,可以發現雖然優化控制的日運行能耗更高,75%冷負荷下單日耗電量增加了248 kW·h,50%冷負荷下單日耗電量增加了3072 kW·h,25%冷負荷下單日耗電量增加了1435 kW·h,但考慮到政府電價調控問題,75%、50%、25%冷負荷下的電費分別為0.527 元、0.410 元、0.314 元,分別低了0.146 元、0.358元、0.451 元,優化控制下的日運行費用整體更低,分別低了2 101.79元、1 397.56 元、1 316.225 元,因此優化控制運行策略仍然較為合理。
4 結束語
本研究提出了基于機場航站樓逐時供冷負荷預測的機場航站樓空調系統運行能耗優化模型,包括多臺制冷機組能耗優化模型、蓄冰罐模型、冷卻塔能耗模型以及最小化運行費用優化模型等,屬于非線性優化控制問題,同時考慮到經濟成本與運行模式最優,可以在不同負荷狀態下確定最優運行策略,且可以有效降低成本支出,滿足優化控制目標。

