多因素下基于路網拓撲的電動汽車充電路徑規劃策略

周箏 龍華 李帥 蔡偉平 梁昌侯

隨著電動汽車產業的發展，電動汽車的充電需求也日益增加.為了滿足電動汽車用戶充電多樣性需求并提高充電設施利用率，本文在考慮出行距離、充電電價以及充電站排隊情況等三種影響因素下構建混合整數線性規劃模型，提出了一種多因素下基于充電站路網拓撲結構的電動汽車充電路徑規劃方法，為用戶規劃充電路徑與充電站選擇.首先，該方法在能耗約束的前提下基于Dijkstra最短路徑算法進行充電引導，為求解多目標最優引入信息熵的概念來確定各參數影響權重.其次，針對用戶充電需求的差異性問題，提出了三種不同目標下的規劃方法以降低用戶充電成本.此外，本文構建了站點隨機充電服務排隊模型并進行敏感性分析以研究充電站服務能力對充電成本的影響.以某地區路網為算例進行仿真，結果表明本文提出的方法能夠有效降低用戶充電出行成本并合理規劃出行路徑，驗證了所提模型的可行性和有效性，對充電選擇和站點配置具有一定的決策參考意義.

電動汽車； 充電路徑； 路網拓撲； 排隊模型； 路徑規劃

TM73; U491 A 2024.017002

Electric vehicles charging path planning method ?based on road network ?under multi parameters

ZHOU Zheng ?1 ， LONG Hua ?1 ， LI Shuai ?1 ， CAI Wei-Ping ?2 ， LIANG Chang-Hou ?1

（1. Faculty of Information Engineering and Automation， Kunming University ?of Science and Technology， Kunming 650500， China;

2. Suzhou Branch Group Information Center （CI）， Bosch （China） Investment Co.Ltd.， Suzhou 215000， China）

With the development of the electric vehicle industry， the charging demand for electric vehicles is also increasing. To meet the diverse charging demand of electric vehicle users and improve the utilization rate of charging facilities， this paper proposes a mixed integer linear programming model considering three influencing parameters： travel distance， charging price and charging station queuing. It then prensents a multi-factor electric vehicle charging path planning method based on the topology of road network to plan the charging path and station selection for users. Firstly， we uses Dijkstra algorithm for charging guidance under the premise of energy consumption constraint， and introduces the concept of information entropy to determine the weight of each parameter for solving the multi-objective optimization. Secondly， to address the variability of users′ charging demand， three planning methods with different objectives are proposed to reduce users′ charging costs. Additionally， this paper constructs a stochastic charging service queue model and conducts sensitivity analysis to investigate the impact of station service capacity on charging cost. Finally， the proposed method is applied to an actual road network for simulation， the results demonstrate that the proposed method can effectively reduce the users′ charging travel cost and reasonably plan the travel path and has certain decision-making significance for charging selection and station configuration.

Electric vehicle; Charging path; Road network topology; Queuing model; Path planning

1 引 言

隨著經濟的發展，汽車行業規模逐漸擴大，汽車數量也與之增長，由此帶來的一系列社會問題尤其是能源安全與環境污染的壓力日益增加 ?［1］ .自我國提出“雙碳”目標以來，綠色出行的方式逐漸被人們所重視.相比于燃油汽車，電動汽車（Electric Vehicle， EV）駕駛用戶在路途中往往會對電池能耗產生焦慮， 同時電動汽車充電基礎設施建設的滯后 ?［1］ 與長時間的充電時長也會進一步加深用戶焦慮，這就是里程焦慮 ?［2］ 問題.因此在考慮控制荷電狀態（State of Charge， SOC）的前提下如何為具有充電需求的電動汽車用戶提供充電引導策略尤為重要.

目前關于電動汽車充電引導與控制策略的研究，一方面集中在電動汽車能耗預測與負載平衡下的充電引導調度.文獻［3］針對電動汽車行駛途中的耗電行為構建動態能耗模型，以剩余電量為約束提出一種考慮出行時間、距離與充電費用的充電路徑規劃策略.文獻［4］分析了電動汽車能耗與出行速度之間的權衡關系.通過引入圖論的思想并改進貝爾曼-福特（Moore-Bellman-Ford）算法，提出了一種以出行時間最優為目標的路徑規劃方法以解決多目標最短路徑問題.文獻［5］提出帶有能量緩沖器的能耗模型來解決電動汽車能耗預測過程中存在的不確定性問題，減少出行途中電量耗盡的概率.文獻［6］提出了雙階段電動汽車充電調度優化方法，以降低用戶成本并實現負荷均衡.文獻［7］提出一種預測決策（Prognostic Decision Making）的方法并構建層次化模型來解決電動汽車隨機最短充電路徑問題.文獻［8］提出了一種模糊自適應大鄰域搜索算法來解決出行過程中不確定性因素對能耗的影響，并將其應用在電動汽車配送出行的路徑引導問題中.文獻［9］提出一種涵蓋路網與充電站位置結構的兩層約束路徑規劃方法，研究電動汽車的充電調度策略.上述研究從整體角度以大規模電動汽車作為研究對象，結合實際交通路網信息進行電動汽車能耗預測來解決最優路徑問題，并未考慮電動汽車個體需求和充電站服務成本對充電引導服務的影響.

另一方面，電動汽車充電站性能配置與服務能力同樣會對電動汽車充電引導服務產生影響.文獻［10］構建充電站排隊模型，研究其對交通路網均衡與用戶路徑選擇的影響.文獻［11］和文獻［12］提出一種混合排隊網絡（Mixed Queueing Network，MQN）來評估站點模型性能與服務質量，同時研究了站點模型參數對阻塞概率的影響.文獻［13］在考慮充換電及車輛到電網放電的多服務模式下，構建電動汽車充換電站排隊與盈利模型，并將模型應用于混合整數線性規劃問題，以實現利潤最大化的目標.文獻［14］以評估充電站服務能力為目標，使用層次分析與廣義熵權法獲取評價分值并構建多服務排隊模型，提出一種結合定性與定量分析的充電站服務能力評價方法.文獻［15］分析了有限長隊列下充電站排隊行為，以總成本最小化為目標優化充電站的位置與容量配置.上述文獻均側重于對充電站性能影響的分析與充電設施的優化，忽略了充電費用和充電服務時間對電動汽車充電引導服務策略的影響.

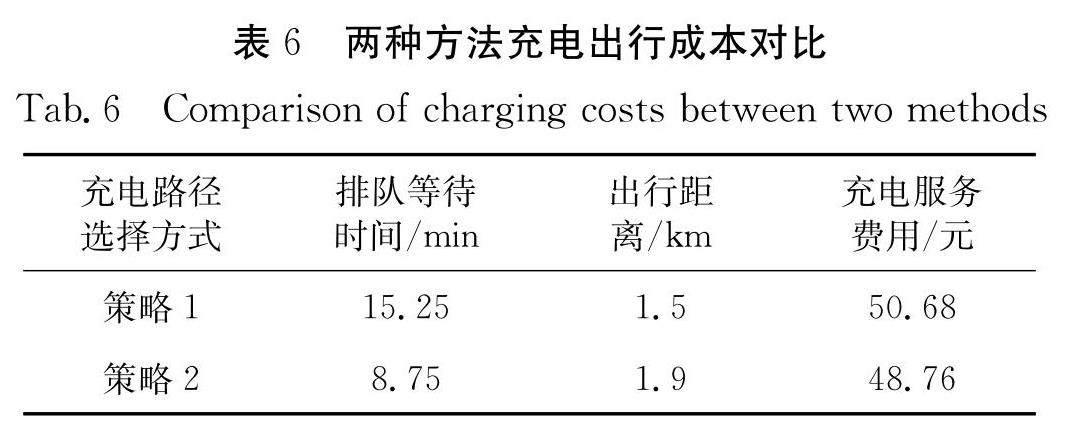
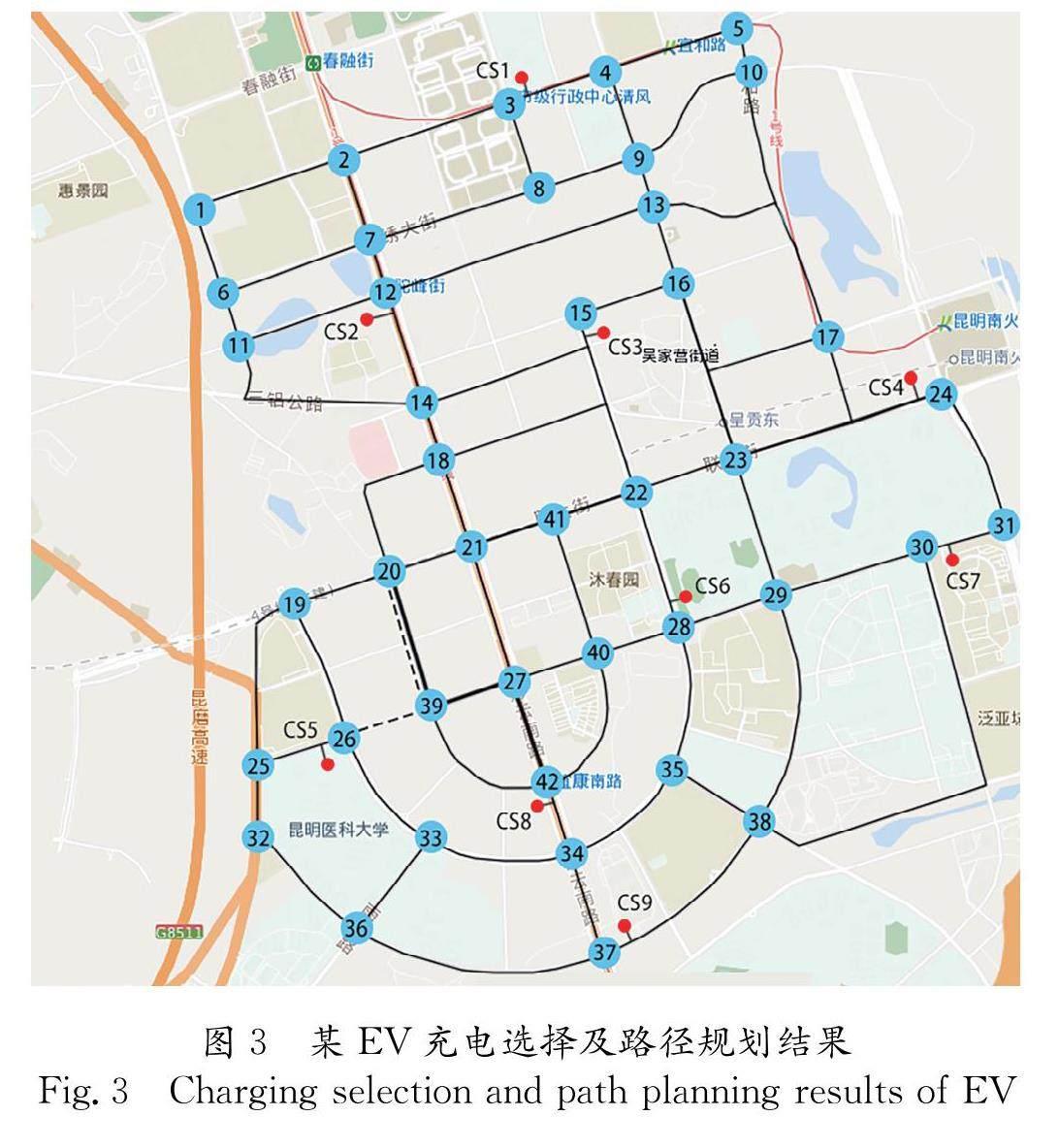
基于上述研究內容，本文建立充電站模型以分析站內配置與服務強度對用戶充電選擇的影響，并從電動汽車用戶個體角度出發，在考慮出行距離、充電電價以及充電設施占用情況三者因素下將電動汽車充電引導服務問題構建為混合整數線性規劃模型，以規劃目標最小化為目的提供充電出行選擇策略，進而減少電動汽車充電出行與充電服務成本.

2 模型建立

電動汽車用戶在選擇充電站進行充電時，除去出行距離與時間外，還需考慮充電站服務成本等因素.為研究充電站性能配置與服務能力對電動汽車充電引導出行的影響，本文建立了充電站時間成本模型與融合充電成本的路網出行成本模型來模擬電動汽車充電出行過程.在分析過程中對模型做出以下假設：

（1） 電動汽車到達充電站的行為受用戶日常用車習慣的影響，具有一定的隨機性.為分析電動汽車的出行特性，現有研究根據真實數據進行分布規律檢驗 ?［16］ 和數量擬合 ?［17］ 得出車輛到達服從泊松分布時準確率較高，基于此，本文假設電動汽車到達充電站的過程服從泊松分布，各個充電站基礎服務設施無差別且充電服務效率相同.

（2） 由于等待充電服務時間過長會提高用戶焦慮度，也會導致電動汽車用戶的服務質量降低 ?［13，18］ ，因此假設電動汽車排隊等待時間存在上限.此外，本文主要研究電動汽車的充電行為，不考慮V2G（Vehicle-to-Grid）技術下車輛到電網的放電行為所帶來的影響.

（3） 電動汽車包括純電動汽車（Battery Electric Vehicle， BEV）和插電式混合動力汽車（Plug-in Hybrid Electric Vehicle， PHEV）.本文研究的電動汽車均為BEV類型且蓄電池最大容量相同.由于大多數電動汽車用戶出行時會保持SOC值在60%以上 ?［19］ ，且電池的放電深度為50%時可將電池損耗降至最低 ?［20］ .為延長電池壽命、提高電池使用的合理性，假設出行過程中當SOC值低于50%時電動汽車存在充電需求.

2.1 充電站時間成本模型

充電站整體服務模式采取先到先服務模式（First Input First Output，FIFO）.在電動汽車充電站 u 內，電動汽車到達使用優先級隊列存儲，充電樁數量為 n u ，充電樁的使用情況用二進制變量 c u 表示，充電樁處于空閑狀態時 c u=0 ，處于使用狀態時 c u=1 .當 ∑c ?u

排隊過程中等待時間上限表明充電站并非無限排隊制模型，等同于站點內存在最大排隊長度即充電站容量的限制.對于充電站 u ，其最大容量 K u 為.

K u=n u+ ?n u δ ?，n u∈

+ 0 ?（1）

其中， ?δ 表示充電樁數量與充電站最大排隊長度的比值，即 ??n u δ ??表示當前充電站的最大隊列長度.電動汽車充電站的服務強度 ρ 定義有

ρ = λ u/n uμ ?（2）

式（2）中， λ u 為充電站 u 的平均到達率， μ 為平均服務率;則 1/λ u 表示車輛到站的平均時間間隔， 1/μ 表示平均充電時間.

根據上述公式結合文獻［15，21］推導可得當前充電站 u 內電動汽車的排隊長度 L u 和平均等待時間 W u ，如下式.

L u= n ?n u ?uρ ?n u+1 P u（0） n u！ （1-ρ） ?2 ×

［1- K u-n u+1 × 1-ρ ρ ?K u-n u - ?ρ ?K u-n u+1 ］ ?（3）

W u= n ?n u ?uρ ?（n u+1） P u 0 ?λn u！ 1- n ?n u ?uρ ?K u ?n u！ P u 0 ???1-ρ ??2 ×

1- K u-n u+1 ?1-ρ ρ ?K u-n u -ρ ?K u-n u+1 ???（4）

式（3）和式（4）中， P u（0） 表示系統處于平穩狀態時，充電站 u 內無電動汽車到達即初始狀態的概率.

P ?u（0）=

∑ ?n ?u-1 ??s=0 ??n ?s uρ ?s s！ + n ??n ?u ?uρ ??n ?u ?1-ρ ??K ?u-n ?u+1 ??n ?u！ 1-ρ ?????-1 ，ρ≠1 ???∑ ?n ?u-1 ??s=0 ??n ?s u s！ + n ??n ?u ?u n ?u！ ?K ?u-n ?u+1 ????-1 ，ρ=1 ??（5）

電動汽車從不同位置選擇不同路徑到達充電站的能耗存在差異，則電動汽車在充電站花費的總時間成本 T u 有

T u=t u+W u ?（6）

式（6）中，充電時間 t u 取決于電動汽車到達充電站 u 時的剩余電量.

2.2 充電出行成本模型

研究路徑選擇問題的基礎是數學圖的構建 ?［5］ .為方便研究電動汽車充電路徑規劃策略，將充電站路網結構抽象簡化為圖的形式來進行數學定義與描述.定義有向賦權圖 G= V，R， Φ ??來表示一組由節點集 V= v 0，v 1，…，v S ?和邊集 R= r 0，r 1，…，r D ?組成的圖拓撲結構，以Φ = φ 0，φ 1，…，φ D ?表示 R 到 V 中元素有序對簇 V×V 的關聯函數，邊集 R 中每條邊 r l 用三元組 ?v s，v d，φ l ?表示，其中 v s，v d∈V 分別表示起始節點和目標節點， φ l 為對應邊成本函數， v s 和 v d 之間的路徑集表示為 h ?s，d ?.對有向賦權圖 G 中 D 條邊對應的邊成本函數進行賦值，可用鄰接矩陣 M= m ?sd ??表示簡化后的圖 G ，式（7）中， m ?sd =∞ 表示節點之間不存在有向邊連接路段;式（8）中， m ?sd ?表示節點 s 和節點 d 之間的距離.

與燃油汽車相比，電動汽車出行途中需考慮電池SOC閾值的約束.傳統路由算法應用在電動汽車背景時，需引入電池電量消耗模型來對電池能耗問題進行約束.因此在路徑集中每條邊所代表的路段上引入路徑能耗參量 E c ，此時路段 r l 在原有邊成本函數的基礎上添加能耗描述路段情況 ???r l= v s，v d，φ l，E c ?.

M= ?0 m ?12 ?∞ … ∞ m ?21 ?0 m ?23 ?… ∞ ∞ m ?32 ?0 … ∞∞ ∞ ∞ … 0 ???（7）

m ?sd = 0， v s=v d

m ?sd ， v s≠v d， r l∈E

∞， v s≠v d，r lE ??（8）

本文建立的路網模型是依據充電站分布情況將充電站節點化為 v u∈V 并引入至路網模型 G ?（V，R， Φ ） ?中.電動汽車到達充電站后至充電服務結束前存在時間成本消耗，因此在路網模型 G ?（V，R， Φ ） ?中的每個充電站節點處引入虛擬節點 v′ u 來表示車輛完成充電服務后的狀態，則虛擬節點與原節點集 V 共同構成集合 V′ 且有 V′={v|v∈V∪v′ u，u=1，2，…} .

如圖1所示，假設電動汽車以 v 0 為源節點， v 2 為目標充電站，則可通過最短路徑尋優的方法來獲取從源節點到目標節點的最短路徑.電動汽車在到達充電站后會在站點耗費一定的時間成本，在每個充電站節點處新增一個節點，二者組合成的節點集用于表示電動汽車到達充電站和離去的兩個狀態，節點之間由虛擬邊 r′ 相連.對原圖 G 的邊集 R 進行擴展，有 R′= r r=R∪r′ ??.虛擬邊的權重取電動汽車在充電站的總時間成本即式（6），圖 G 中原邊成本集擴展后有Φ ′= φ φ= Φ ∪Τ u ??.

2.3 能耗模型

城市道路等級通常劃分為快速路、主干路、次干路和支路等四級.道路等級的差異會影響電動汽車的電能消耗.文獻［22］根據實際數據建立能耗模型以計算電動汽車單位距離能耗，如式（9）.

E 1 c=0.247+1.520V ?ev_s ????-1 -0.004V ?ev_s +

2.992×10 ?-5 V ?ev_s ?E 2 c=-0.179+0.004V ?ev_s +5.492V ?ev_s ????-1 ?E 3 c=0.21-0.001V ?ev_s +1.531V ?ev_s ????-1 ?E 4 c=0.208-0.002V ?ev_s +1.553V ?ev_s ??-1 ???（9）

式（9）中， E 1 c、E 2 c、E 3 c、E 4 c 分別表示電動汽車途徑道路等級為快速路、主干路、次干路和支路時的單位距離能耗; V ?ev_s ?為電動汽車平均速度， E c 表示電動汽車出行路徑總能耗.此時電動汽車的剩余電量如式（10）和式（11）所示.

B r=B ??init ?-E c ?（10）

ΔE=BC-B r ?（11）

其中， B r 表示電池剩余電量; B ??init 為初始電量; ΔE 表示充電電量; BC 為電池容量，單位均為kW·h.

2.4 動態定價模型

電動汽車充電入網后產生的負荷在高峰期可能會對電網穩定性產生一定影響，現階段主要采用峰谷分時電價的方法，依據一天內電網使用情況來劃分峰、谷時段，并按時段設定不同的電價以達到引導用戶充電的目的 ?［23］ .但用戶側負荷需求會受到地域環境等變化的影響，擁堵的變化可能會造成需求負荷與電價在峰谷值不匹配的情況.因此本文提出一種基于充電擁擠度的定價模型，如式（12）～式（14）所示.

p ?u，t =p t+β tp f ?（12）

β t=L u/K u ?（13）

p t = ?0.76， t∈（23 ∶ 00，7 ∶ 00）

0.95， t∈（7 ∶ 00，10 ∶ 00）∪

（12 ∶ 00，18 ∶ 00）∪（21 ∶ 00，23 ∶ 00）

1.18， t∈（10 ∶ 00，12 ∶ 00）∪

（18 ∶ 00，21 ∶ 00） ??（14）

式（12）中， p ?u，t ?為充電站 u 在當前時刻 t 的電價，由基礎電價 p t 和浮動電價 p f 組成； ?β t 表示當前時刻站內充電擁擠度.其中基礎電價受峰谷時段的影響，峰時段為10∶00-12∶00、18∶00-21∶00，谷時段為23∶00-7∶00，其余為平時段 ?［6，24］ ，各時段的電價見式（14）.

3 電動汽車充電引導規劃模型

3.1 目標函數

電動汽車充電出行選擇受到多因素影響.本文在考慮出行距離、充電電價和充電站使用情況的因素下構建混合整數線性規劃模型，目標函數如式（15）所示.考慮到用戶的充電出行需求存在差異，對影響因素采用賦權處理以滿足不同用戶需求.

min ［w 1∑ ?l∈h ??s，d ??φ ?l v ?s，v ?d y v ?s，v ?d η ?SOC ???v ?s，v ?d +

w 2p ??u，t ΔEc ?uc ?type ??u+w 3c ?I u］ ?（15）

s.t. ?∑ ?v ?i，v ?j∈V ?y v ?i，v ?j -y v ?j，v ?i = ?1， -1， 0， ??v ?i=v ?s v ?i=v ?d 其他 ???（16）

式（15）中， w 1，w 2，w 3 為不同影響因素的權重系數，第一項表示電動汽車出行成本， η ??SOC ???v s，v d ?表示電動汽車能耗約束， η ??SOC ???v s，v d =1 時電動汽車剩余電量足夠到達充電站;第二項為電動汽車充電價格成本，其中 c ??type ??u 為二進制變量用于表示電動汽車充電類型： c ??type ??u=1 表示快充服務， c ??type ??u=0 表示慢充服務;第三項為充電時間成本， c I u 為充電站 u 的充電樁使用空閑率.式（16）中 y v s，v d ?為用于描述路徑選擇約束的二進制變量，當電動汽車出行路徑包含邊 r l v s，v d ?時 y v s，v d =1 .

3.2 結合權重的目標函數計算

信息熵可以衡量各因素指標在評價中的重要性，并從客觀角度來過濾原始數據中的冗余信息 ?［14］ ，從而構造權重進行決策的評價分值計算.通過引入信息論中信息熵的概念，能夠從客觀角度來衡量指標，并將不同影響因子的內部差異以信息量的形式進行表達.電動汽車用戶在選擇充電站時各影響因素在性質和量綱等上面存在一定差異，因此首先需要對各指標數據進行無量綱化處理.設充電站數量為 u ，影響因子數為 q ，初始決策矩陣 X= x ?ij ??有

X= ?x ?11 ?x ?12 ?… x ?1q ?x ?21 ?x ?22 ?… x ?2q ?x ?u1 ?x ?u2 ?… x ?uq ????（17）

為消除量綱影響對矩陣 X 進行標準化處理 ?［25］ ，如式（18）～（23）所示.式（18）根據效率型和成本型影響因素對 x ?ij ?分別進行標準化以得到 x * ?ij ?，其中 ??x ?ij ???j ??min ??表示第 j 項因子下的最小值， ??x ?ij ???j ??max ??同理;式（19）分別計算第 j 項指標下第 i 個節點所占比重得到對應概率 p ?ij ?;式（20）、式（21）計算出各指標對應的信息熵 E j 與信息效用值 I j ;式（22）中 w j 即為基于信息熵計算得出的各影響因素權重系數，且 ∑ ?q ??j=1 w ?j=1.

使用熵權法計算獲得的權重具有一定的適應性 ?［14］ ，三種影響因素的偏重存在差異導致其分別適應于不同的權重系數，權重系數值越大表明電動汽車用戶對應影響因素的需求越大.將無量綱化后的數據賦予權重來計算目標成本以作為評價分值 S j ，如式（23）所示，即可確定每個站點的影響因素成本并進行充電路徑的優先級選擇.

x * ?ij = x ?ij - ?x ?ij ???j ??min ????x ?ij ???j ??max ?- ?x ?ij ???j ??min ???x * ?ij = ??x ?ij ???j ??max ?-x ?ij ???x ?ij ???j ??max ?- ?x ?ij ???j ??min ??????（18）

p ??ij =x ?* ?ij /∑ u ?i=1 ?x * ??ij ??（19）

E ?j=- 1 ?ln u ∑ u ?i=1 ?p ??ij ?ln p ??ij ??（20）

I j=1-E j ?（21）

w ?j=I ?j/∑ u ?i=1 ?I ?j ?（22）

S ?j=∑ q ?j=1 ?w ?jx * ??ij ??（23）

3.3 電動汽車充電出行路徑規劃流程

根據上節內容，可將式（15）描述的規劃問題在增加耗電量約束條件的前提下使用Dijkstra算法思想進行求解.

Step 1 ???輸入涵蓋充電站分布的路網拓撲圖鄰接矩陣 M 、道路參數與充電站參數.

Step 2 ???仿真模擬生成電動汽車的初始位置 v s 、初始電量 B ?init ?、出發時間 t 和平均速度 V ?ev_s ?.

Step 3 ???確定源點集 V s 和可選目標充電站點集 V d .通過Dijkstra算法計算以源點集 V s 中每個元素 v s∈V s 為起點到達可選目標站點集合中的所有站點的最短路徑 h ?s，d ?，并計算各路徑對應距離 m ?sd ?，得到源點到可選目標充電站點的最短距離矩陣 M′ .

Step 4 ???根據能耗模型計算電動汽車到達各個目標充電站的路徑總能耗 E c ，通過式（10）獲取剩余電量，并結合能耗約束條件判斷電動汽車能否到達各個目標充電站點;對目標點集 V d 進行遍歷，若未滿足能耗約束令對應路徑 h ?s，d ?的最短距離 ?m′ ?sd = ∞ ，否則繼續遍歷直至結束.保留能耗約束下能夠到達的充電站節點并移除 m′ ?sd = ∞的站點，更新最短距離矩陣 M′ 和目標充電站點集 V′ d .

Step 5 ???獲取當前時刻對應的基礎電價 p t 并計算電價 p ?u，t ?.根據最短距離 m′ ?sd ?，各個充電站電價 p ?u，t ?和使用空閑率 c I u 三種影響因素的原始數據進行無量綱化處理，根據式（22）計算獲得各指標的權重集合 w j={w 1，w 2，w 3} .

Step 6 ???根據權重集合 w j 求解式（15）混合整數線性規劃模型，獲得模型最優解.根據最優解結果確定充電站的選擇并根據式（4）、式（10）和式（11）計算電動汽車用戶到達充電站 u 后預計等待時間 W u 和充電費用 p ?u，t ΔE 并返回 （m′ ?sd ，h ?s，d ，W u， ??p ?u，t ΔE） .

4 仿真分析

4.1 仿真參數

本文使用Python3.7對所建立模型進行仿真模擬.模型選取昆明市某區域作為研究區域，占地面積約25.98 ??km ??2 ，路網結構與道路參數均使用GIS軟件從百度地圖中提取，區域內共具有42個節點和77條道路，涵蓋9個充電站，如圖2所示.根據路網結構依據圖論思想構建拓撲圖并提取鄰接矩陣，如表1所示.具體道路參數如表2所示.

充電站模型仿真時間以小時為單位按全天24 h進行仿真，慢充功率為10 kW，快充功率為30 kW，充電效率均為90%;設置電動汽車電池容量均為60 kW·h，初始電量隨機選取SOC的10%～50%.各個充電站的服務率均為0.33，具體參數設置如表3所示.

4.2 仿真分析

4.2.1 基于多目標成本的充電規劃結果分析 ?以某電動汽車用戶個體為例，設置在兩種不同的充電規劃策略下電動汽車均在起始節點 v ?20 ?出發，起始時間為17∶00.策略1設置為就近策略選擇充電站點 ?［26］ ;策略2設置為采用多目標規劃策略即本文規劃方法，在綜合考慮多因素的前提下根據混合整數線性規劃模型選擇最優站點進行充電.在剩余電量約束的前提下，各影響因素的計算權值見表4.

由表4可知各影響因素的權值.從當前起點 v ?20 ?到達各個充電站的路徑規劃與對應目標值如表5所示.根據目標函數值可以看出，用戶充電出行的最優選擇是 cs ?8充電站.具體路徑如圖3所示，虛線標注路段表示策略1下的充電站點選擇與行駛路徑;粗實線標注路段表示策略2下的充電站點選擇與形式路徑.不同策略的充電出行成本如表6所示.

從表6中可以看出，使用該規劃策略致使電動汽車出行距離增加，但充電排隊等待時間減少了42.6%，充電服務費用減少了5.8%，說明在綜合多目標因素的影響下該方法能夠從綜合角度考慮，提高電動汽車路徑規劃的合理性.

4.2.2 基于用戶需求的規劃結果分析 ?不同電動汽車用戶充電出行需求不同.為滿足場景多元化對式（12）中的參數 ?w 1，w 2，w 3 ?從主觀角度進行調整.三種目標場景下電動汽車用戶均以 v ?20 ?作為起始節點，充電出行路徑規劃后結果如表7.

從表7可看出，電動汽車用戶不同的充電需求產生的規劃結果偏重不同.場景1中用戶充電出行偏重于出行距離最短，相比于場景2和場景3能看出場景1下出行距離分別下降60.5%，44.4%;場景2中用戶充電出行偏重于充電費用最低，可以看出充電服務費用這一因素場景2相比于場景1和場景3降低了6.1%，7.0%;場景3充電出行偏重于排隊站等待時間最短，相比于場景1和場景2的充電排隊等待時間減少了71.9%，63.8%.從實驗結果可看出，所提出的電動汽車用戶充電出行引導規劃模型能夠較好地適應不同用戶的需求以進行充電選擇.

4.2.3 充電站模型參數的敏感性分析 ?充電站的服務強度易受到充電站基礎設施配置的影響，而充電排隊時間與服務能力有關，充電排隊時間的變化影響到用戶充電時間成本;同樣充電站電價的變化也會對充電費用成本產生一定影響.由于路網拓撲中充電站的位置已固定，故本節在保持出行成本不變的基礎上，通過對充電站模型參數與充電電價和排隊時間的權重比值進行敏感性分析，以研究充電成本對電動汽車用戶充電出行引導策略的影響.

保持路網拓撲與充電站點位置不變，通過改變電價與排隊時間因素的權重比值來探討其對充電成本的影響.圖4給出了 w 2 和 w 3 比值分別設置為 w 2∶w 3∈ 1∶1，1∶3，1∶5，1∶7，1∶9 ?時增加站點流量對目標函數結果的影響，從圖4可看出，不同權重比值整體趨勢均為隨著充電站充電流量的增加致使目標函數結果逐漸增加，且5組權重比值呈現相同增長趨勢.當權重比值為 w 2∶w 3=1∶3 時目標結果變化幅度最大;之后隨著權重 w 3 的增大結果變化幅度逐漸縮小，表明在權重比值達到1∶3時能夠有效減少充電成本，隨后增加權重比值對充電成本的影響逐漸減小.這說明在實際應用中保持出行距離不變的前提下，充電站的電價與服務能力的影響比重會對用戶充電行為產生影響，可根據此在考慮經濟效益的前提下設置充電站電價與基礎設施配置.

由式（2）和式（4）易知，充電站內的樁數的設置會影響充電站的服務能力，進而影響充電站排隊等待時間.圖5描述了不同到達率下電動汽車充電排隊等待時間對充電站樁數設置的敏感性.從圖5可以看出，隨著充電站樁數的增加充電服務能力逐漸增強，電動汽車的充電平均等待時間整體呈下降趨勢，且下降斜率逐漸減少，最終趨于平緩.此外到達率為0.79時隨著樁數的增加下降趨勢相比于其他到達率更早趨于平緩狀態.該結果說明充電站可通過安裝更多的充電樁以減少排隊等待時間，而增加充電樁數對服務能力的提高有限，在實際應用中可考慮充電樁成本的基礎上結合充電站流量來合理設置站點樁數，在提高用戶充電服務質量的同時盡可能提高利用率.

5 結 論

本文研究了電動汽車在多種因素影響下的充電路徑規劃問題，針對該問題文中構建了混合整數線性規劃模型來解決包括用戶出行成本和充電成本最優的多目標規劃問題.考慮到不同用戶具有不同出行需求，對三種目標狀態下進行最優充電選擇規劃以滿足用戶需求差異性.仿真證明該方法能夠較好地達到綜合目標最優，并能夠有針對性地根據用戶需求差異進行充電規劃選擇以降低相應成本.此外，在充電站點及出行成本固定的情況下，文中構建了站點隨機充電服務排隊模型以模擬充電服務過程，并對站內服務強度和基礎設施配置進行敏感性分析以研究其對用戶出行成本的影響，為提高充電站配置的合理性提供了參考.

本文目前研究主要在路網拓撲結構上結合能耗約束為用戶提供充電選擇并規劃出行路徑，未考慮對用戶充電行為進行分析以獲取其偏好.未來將結合實際充電站數據和出行數據以開展用戶行為習慣挖掘，進一步驗證模型的合理性，同時以站點選址與設施優化為方向進行下一步研究.

參考文獻：

［1］ ??Ma J， Lyu X D， Chen Y S， ?et al . Current status and countermeasures for Chinas new energy automobile industry and technology development ［J］. China J Highw Transp， 2018， 31： 1.［馬建， 劉曉東， 陳軼嵩， 等. 中國新能源汽車產業與技術發展現狀及對策［J］. 中國公路學報， 2018， 31： 1.］

［2］ ?Noel L， de Rubens G Z， Sovacool B K， ?et al . Fear and loathing of electric vehicles： The reactionary rhetoric of range anxiety ［J］. ERSS， 2019， 48： 96.

［3］ ?Su ?S， Yang T T， Li Y J， ?et al . Charging route planning for electric vehicles considering real-time dynamic energy consumption ［J］. AEPS， 2019， 43： 136.［蘇粟， 楊恬恬， 李玉璟， 等. 考慮實時動態能耗的電動汽車充電路徑規劃［J］. 電力系統自動化， 2019， 43： 136.］

［4］ ?Morlock F， Rolle B， Bauer M， ?et al . Time optimal ro-uting of electric vehicles under consideration of available charging infrastructure and a detailed consumption model ［J］. IEEE T Intell Transp， 2020， 21： 5123.

［5］ ?Huber G， Bogenberger K， van Lint H. Optimization of charging strategies for battery electric vehicl-es under uncertainty［J］. IEEE T Intell Transp， 2022， 23： 760.

［6］ ?Luo W X， Chang X Q， Fu R， ?et al . Charging-discharging scheduling strategy for electric vehicles considering supply and demand ［J］. P CSU-EPSA， 2022， 34： 106.［羅維祥， 常喜強， 伏睿， 等. 考慮供需需求的電動汽車充放電調度策略［J］. 電力系統及其自動化學報， 2022， 34： 106.］

［7］ ?Rozas H， Munoz-Carpintero D， Saez D， ?et al . Solving in real-time the dynamic and stochastic shortest path problem for electric vehicles by a prognost-ic decision making strategy［J］. Expert Syst Appl， 2021， 184： 115489.

［8］ ?Zhang S， Chen M， Zhang W， ?et al . Fuzzy optimization model for electric vehicle routing problem with time windows and recharging stations［J］. Expert Syst Appl， 2019， 145： 113123.

［9］ ?Zhang Y， Wu B， Chiang Y Y， ?et al . BiS4EV： a fast routing algorithm considering charging stations ?and preferences for electric vehicles［J］. Eng Appl Artif Intel， 2021， 104： 104378.

［10］ ?Li H， Chen H. Mixed traffic network equilibrium with battery electric vehicles considering charging queuing time ［J］. J Jilin Univ（Technol Ed）， 2021， 51： 1684.［李浩， 陳浩. 考慮充電排隊時間的電動汽車混合交通路網均衡［J］. 吉林大學學報（工學版）， 2021， 51： 1684.］

［11］ Tan X， Sun B， Wu Y， ?et al . Asymptotic performance e-valuation of battery swapping and charging stati-on for electric vehicles［J］. Perform Evaluation， 2018， 119： 43.

［12］ Tan X， Sun B， Tsang D. Queueing network models for electric vehicle charging station with battery swapping［C］//IEEE International Conference on ?Smart Grid Communications. ［S.l.］： IEEE， 2015.

［13］ Esmailirad S， Ghiasian A， Rabiee A. An extended M/M/K/K queueing model to analyze the profit of a multiservice electric vehicle charging station［J］. ?IEEE T Ven Technol， 2021， 70： 3007.

［14］ Sheng R， Tang Z， Xue J C. Dynamic evaluation method of EV charing station service capability under multi indicators ［J］. P CSEE， 2021， 41： 4891.［盛銳， 唐忠， 薛佳誠. 多指標下EV充電站服務能力動態評價方法［J］. 中國電機工程學報， 2021， 41： 4891.］

［15］ Xiao D， An S， Cai H， ?et al . An optimization model for electric vehicle charging infrastructure pl-anning considering queuing behavior with finite queue length ［J］. J Energ Storage， ?2020， 29： 101317.

［16］ Zhang D， Jiang J C， Zhang W G， ?et al. ?Optimal configuration of charing spots for electric taxis ［J］. Trans China Electrotech Soc， 2015， 30： 181.［張帝， 姜久春， 張維戈， 等. 電動出租車充電樁優化配置［J］. 電工技術學報， 2015， 30： 181.］

［17］ Yu J W， Sun Y L， Zhang X D. Charging load forecasting considering the unbalanced development of EV ［J］. Electr Meas Instrum， 2019， 56： 43.［余軍偉， 孫云蓮， 張笑迪. 考慮發展不均衡的電動汽車充電負荷預測［J］. 電測與儀表， 2019， 56： 43.］

［18］ Kumar N， Kumar T， Nema S， ?et al . A comprehensive planning framework for electric vehicles fast charging station assisted by solar and battery based on Queueing theory and non-dominated sorting genetic algorithm-Ⅱ in a coordinated transportation and power network ［J］. J Energ Storage， 2022， 49： 104180.

［19］ Yan Y J， Zha W X， Shi J G， ?et al . Mixed network equilibrium model with stochastic charging demand ［J］. J Jilin Univ（Technol Ed）， 2022， 52： 136.［閆云娟， 查偉雄， 石俊剛， 等. 具有隨機充電需求的混合動態網絡平衡模型［J］. 吉林大學學報（工學版）， 2022， 52： 136.］

［20］ Ge S Y， Li R， Han J， ?et al . Charging station planning considering probability behavior characteristic of electric taxi ［J］. AEPS， 2016， 40： 50.［葛少云， 李榮， 韓俊， 等. 考慮電動出租車隨機概率行為特性的充電站規劃［J］. 電力系統自動化， 2016， 40： 50.］

［21］ Li R Q， Su H Y.Optimal allocation of charging facilities for electric vehicles based on queuing theory ［J］. AEPS， 2011， 35： 58.［李如琦， 蘇浩益. 基于排隊論的電動汽車充電設施優化配置［J］. 電力系統自動化， 2011， 35： 58.］

［22］ Song Y Y. Energy consumption modeling and cruising range estimation based on driving cycle for electric vehicles ［D］. Beijing： Beijing Jiaotong University， 2014.［宋媛媛. 基于行駛工況的純電動汽車能耗建模及續駛里程估算研究［D］. 北京： 北京交通大學， 2014.］

［23］ Deng H Q， Zhang X F， Zeng J F， ?et al . Orderly charging and discharging scheduling strategy of electric vehicle based on dynamic TOU price ［J］. J Hebei Univ Sci Tech， 2022， 43： 240.［鄧慧瓊， 張曉飛， 曾凡淦， 等. 基于動態分時電價的電動汽車有序充放電調度策略［J］. 河北科技大學學報， 2022， 43： 240. ］

［24］ Cao F， Hu J T， Luo J B， ?et al . Capacity configuration of fast charging stations based on EV path simulation under dynamic model of transportation network ［J］. Electr Pow Autom Eq， 2022 42： 107.［曹昉， 胡佳彤， 羅進奔， 等. 基于路網動態模型下EV路徑模擬的快速充電站容量配置［J］. 電力自動化設備， 2022 42： 107.］

［25］ Yu X Y， Wei J L， Wei Y L， ?et al . Study on the decision of airport taxi drivers based on income priority ［J］. J Sichuan Univ（Nat Sci Ed）， 2020， 57： 689.［俞雪永， 魏金嶺， 魏弋力， 等. 基于收益優先的機場出租車司機決策研究［J］. 四川大學學報（自然科學版）， 2020， 57： 689.］

［26］ Duan P P， Liu L. Design and research of intelligent charging station management system ［J］. Computer Tech Dev， 2019， 29： 200.［段芃芃， 劉鋰. 智能充電站管理系統設計與研究［J］. 計算機技術與發展， 2019， 29： 200.］

收稿日期： ?2022-09-04

基金項目： ?國家自然科學基金（61761025）

作者簡介： ??周箏（1998-）， ?女， ?河南平頂山人， 碩士研究生， 研究方向為數據處理與建模仿真. E-mail： ria_zhou.km@foxmail.com

通訊作者： ?龍華. E-mail： 1670931890@qq.com