從整體和局部的關(guān)系學(xué)習(xí)相似

第六章 圖形的相似

領(lǐng)" 銜" 人：諸士金

組稿團(tuán)隊(duì)：江蘇省南京市鼓樓區(qū)教師發(fā)展中心

“相似的圖形”這一章重點(diǎn)研究相似，尤其是三角形相似的相關(guān)知識(shí)。而在學(xué)習(xí)本章之前，同學(xué)們已經(jīng)完整地經(jīng)歷了對全等圖形、三角形全等的探索和認(rèn)識(shí)，掌握了三角形全等的性質(zhì)與判定，而全等圖形是特殊的相似圖形。因此，本章就可以通過“類比、猜想、推理”的方法，利用“探索三角形全等的條件”學(xué)習(xí)策略，探索三角形相似的條件和相似三角形的性質(zhì)。

整體看，從全等，到相似，再到位似，體現(xiàn)了“特殊——一般——特殊”的過程。在本章學(xué)習(xí)的最后階段，我們還會(huì)學(xué)習(xí)如何運(yùn)用相似三角形的知識(shí)解決實(shí)際問題，這清晰地體現(xiàn)了研究幾何圖形的“判定——性質(zhì)——運(yùn)用”的主線。在這一主線的學(xué)習(xí)過程中，整體認(rèn)識(shí)變化，局部厘清關(guān)系，可以為研究圖形相似的判定和性質(zhì)提供更好的理解視角。

一、從局部到整體，學(xué)習(xí)圖形相似的判定

在本章學(xué)習(xí)中，我們通過探索可以發(fā)現(xiàn)“兩角分別相等的兩個(gè)三角形相似”“兩邊成比例且夾角相等的兩個(gè)三角形相似”“三邊成比例的兩個(gè)三角形相似”。這三個(gè)判定定理都是從構(gòu)成三角形的基本元素的關(guān)系出發(fā)進(jìn)行判定的，其共性是從“局部”到“整體”。以此類推，我們可以嘗試從三角形其他的局部元素出發(fā)進(jìn)行組合，并研究是否能夠判定兩個(gè)三角形相似，如例1。

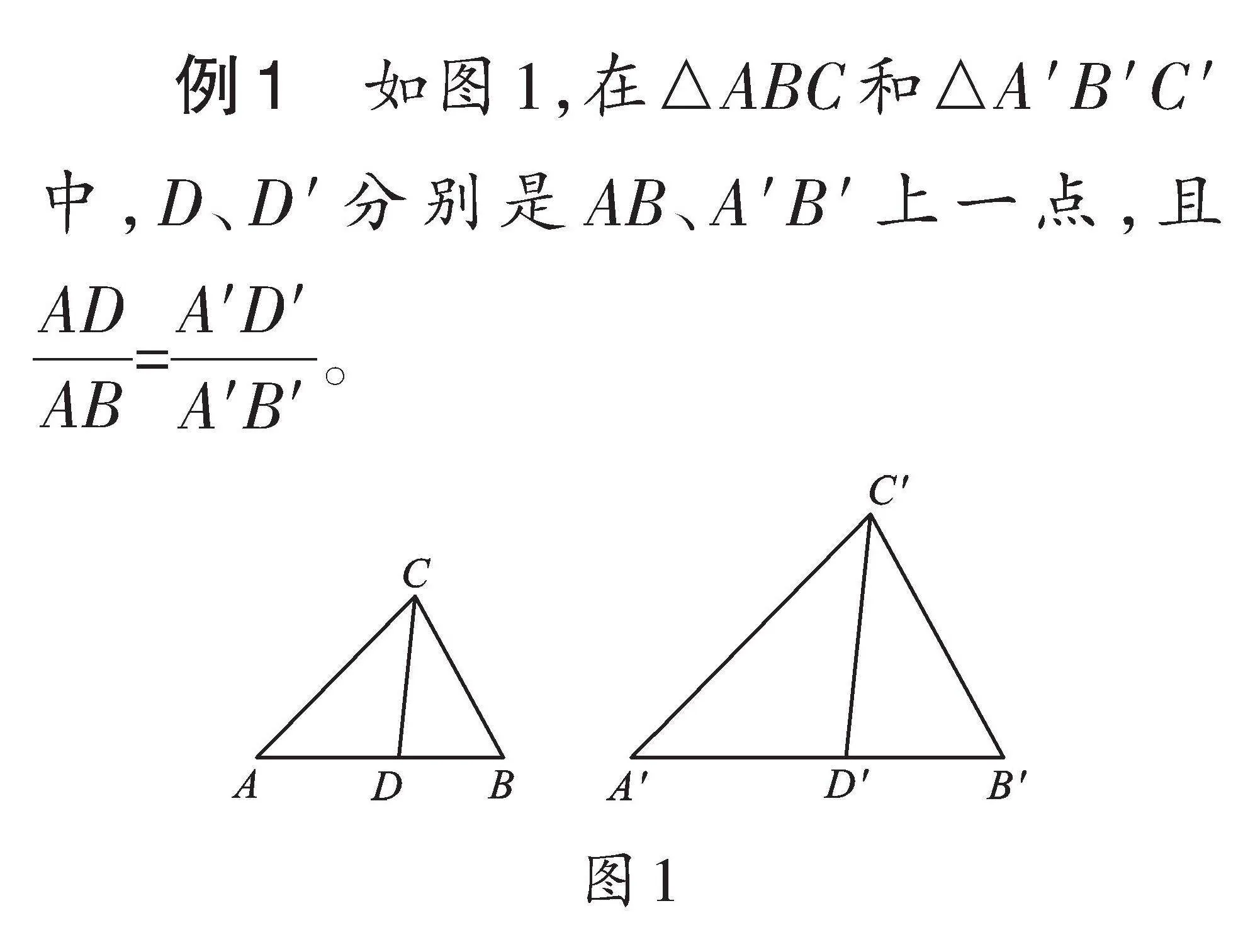
例1 如圖1，在△ABC和△A′B′C′中，D、D′分別是AB、A′B′上一點(diǎn)，且[ADAB]=[A′D′A′B′]。

（1）當(dāng)[CDC′D′]=[ACA′C′]=[ABA′B′]時(shí)，判斷△ABC與△A′B′C′是否相似，并說明理由。

（2）當(dāng)[CDC′D′]=[ACA′C′]=[BCB′C′]時(shí)，判斷△ABC與△A′B′C′是否相似，并說明理由。

【解析】（1）△ABC與△A′B′C′相似。

∵[ADAB]=[A′D′A′B′]，

∴[ADA′D′]=[ABA′B′]。

又∵[CDC′D′]=[ACA′C′]=[ABA′B′]，

∴[CDC′D′]=[ACA′C′]=[ADA′D′]。

∴△ADC∽△A′D′C′。

∴∠A=∠A′。

∵[ACA′C′]=[ABA′B′]，

∴△ABC∽△A′B′C′。

（2）△ABC與△A′B′C′相似。

如圖2，過點(diǎn)D、D′分別作DE∥BC、D′E′∥B′C′，DE交AC于點(diǎn)E，D′E′交A′C′于點(diǎn)E′。

∵DE∥BC，∴△ADE∽△ABC。

∴[ADAB]=[DEBC]=[AEAC]。

同理[A′D′A′B′]=[D′E′B′C′]=[A′E′A′C′]。

又[ADAB]=[A′D′A′B′]，∴[DEBC]=[D′E′B′C′]。

∴[DED′E′]=[BCB′C′]。同理[AEAC]=[A′E′A′C′]。

∴[AC-AEAC]=[A′C′-A′E′A′C′]，

即[ECAC]=[E′C′A′C′]。

∴[ECE′C′]=[ACA′C′]。

又[CDC′D′]=[ACA′C′]=[BCB′C′]，

∴[CDC′D′]=[DED′E′]=[ECE′C′]。

∴△DCE∽△D′C′E′。

∴∠CED=∠C′E′D′。

∵DE∥BC，∴∠CED+∠ACB=180°。

同理∠C′E′D′+∠A′C′B′=180°。

∴∠ACB=∠A′C′B′。

又[ACA′C′]=[BCB′C′]，

∴△ABC∽△A′B′C′。

我們從例1的解析過程可以看到，判定兩個(gè)圖形之間的關(guān)系，并不一定要從構(gòu)成圖形的基本元素出發(fā)，還可以從圖形的其他相關(guān)元素出發(fā)。在滿足一定條件以及這些相關(guān)元素局部關(guān)系的共同作用下，也能判定整體的關(guān)系。類似的，我們可以繼續(xù)研究一些變式：

如圖3，在△ABC和△A′B′C′中，D、D′分別是AB、A′B′上一點(diǎn)，且[ADAB]=[A′D′A′B′]。

變式1 當(dāng)[CDC′D′]=[ACA′C′]，∠ACD=∠A′C′D′時(shí)，判斷△ABC與△A′B′C′是否相似，并說明理由。

變式2 當(dāng)[CDC′D′]=[ACA′C′]，∠BCD=∠B′C′D′時(shí)，判斷△ABC與△A′B′C′是否相似，并說明理由。

變式3 當(dāng)[CDC′D′]=[ACA′C′]，∠A=∠A′時(shí)，判斷△ABC與△A′B′C′是否相似，并說明理由。

……

這樣的變式，同學(xué)們有興趣的話可以研究一下。如果不能判斷兩個(gè)三角形相似，請大家嘗試舉反例說明。

二、從整體到局部，學(xué)習(xí)圖形相似的性質(zhì)

結(jié)合對圖形相似判定的理解來研究圖形相似的性質(zhì)，具體體現(xiàn)在局部元素之間的關(guān)系上，比如“相似三角形的對應(yīng)邊成比例、對應(yīng)角相等”“相似三角形的對應(yīng)線段的比等于相似比”等。這些性質(zhì)的學(xué)習(xí)價(jià)值不僅表現(xiàn)為對兩個(gè)相似三角形在整體變化中的對應(yīng)元素關(guān)系的認(rèn)知，而且表現(xiàn)為“性質(zhì)”的共性價(jià)值——應(yīng)用。

例2 如圖4，AC與BD交于點(diǎn)O，OA=OD，∠ABO=∠DCO，E為BC延長線上一點(diǎn)，過點(diǎn)E作EF∥CD，交BD的延長線于點(diǎn)F。

（1）求證：△AOB≌△DOC；

（2）若AB=2，BC=3，CE=1，求EF的長。

【解析】（1）證明：∵∠ABO=∠DCO，∠AOB=∠DOC，OA=OD，

∴△AOB≌△DOC（AAS）。

（2）解：∵BC=3，CE=1，

∴BE=BC+CE=4。

∵△AOB≌△DOC，∴CD=AB=2。

∵CD∥EF，∴△BCD∽△BEF。

∴[BCBE]=[CDEF]。

∴EF=[BE·CDBC]=[4×23]=[83]。

從整體到局部，學(xué)習(xí)相似三角形的性質(zhì)，是整體決定局部的體現(xiàn)。兩個(gè)圖形相似，既可以看成圖形整體形狀相同，也可以看成由一個(gè)圖形進(jìn)行相似變化（擴(kuò)大或縮小）得到另一個(gè)圖形。因此，研究圖形相似的性質(zhì)也可以理解為整體圖形在相似變化中局部元素關(guān)系中的變中不變性以及變中有序性。

三、從整體去理解全等與相似的一致性

在初中階段，我們重點(diǎn)研究的是三角形相似，而研究三角形相似可以類比三角形全等的學(xué)習(xí)路徑。

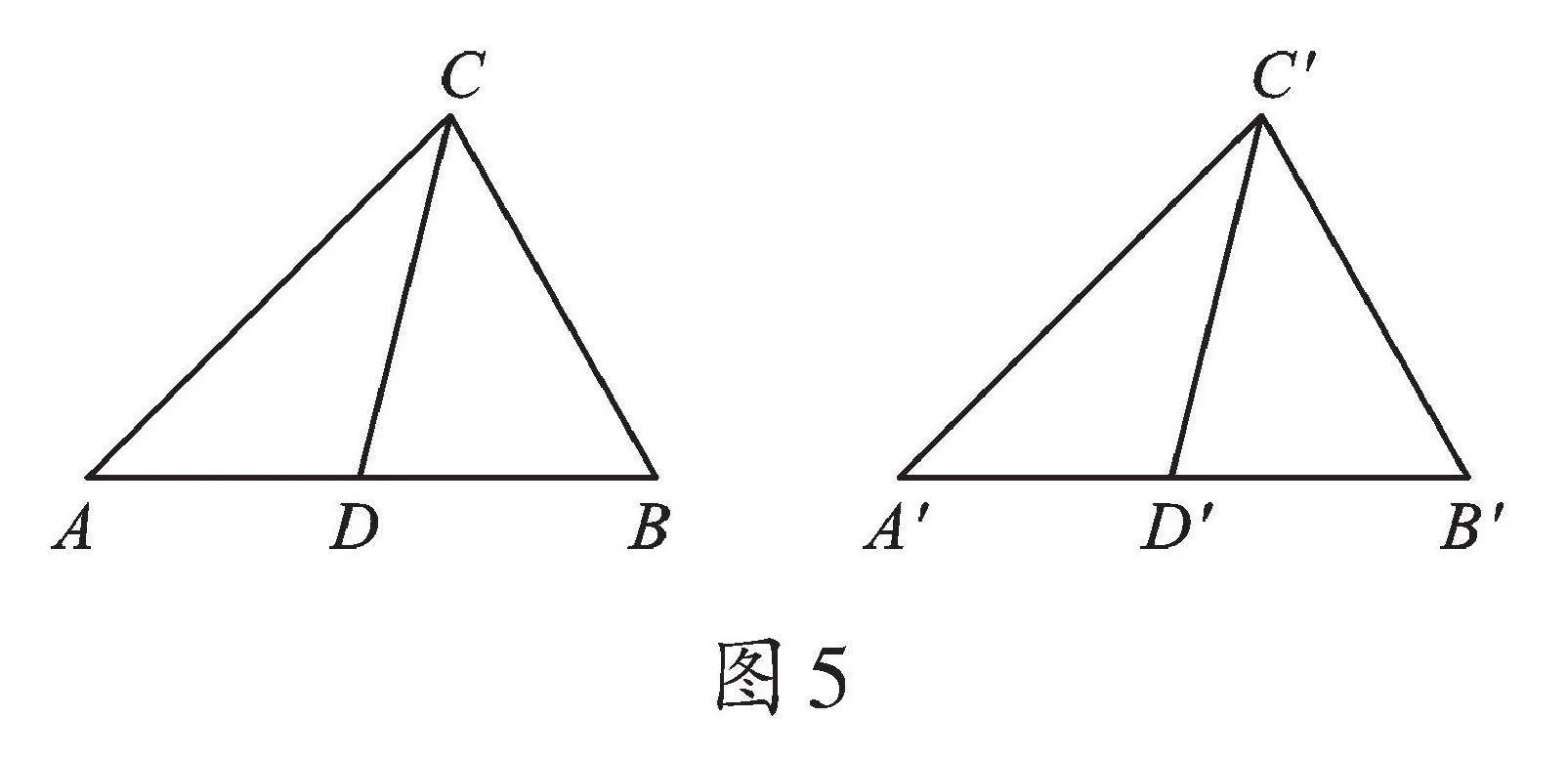
例3 如圖5，在△ABC和△A′B′C′中，D、D′分別是AB、A′B′的中點(diǎn)。若CD=C′D′，AC=A′C′，BC=B′C′，判斷△ABC與△A′B′C′是否全等，并說明理由。

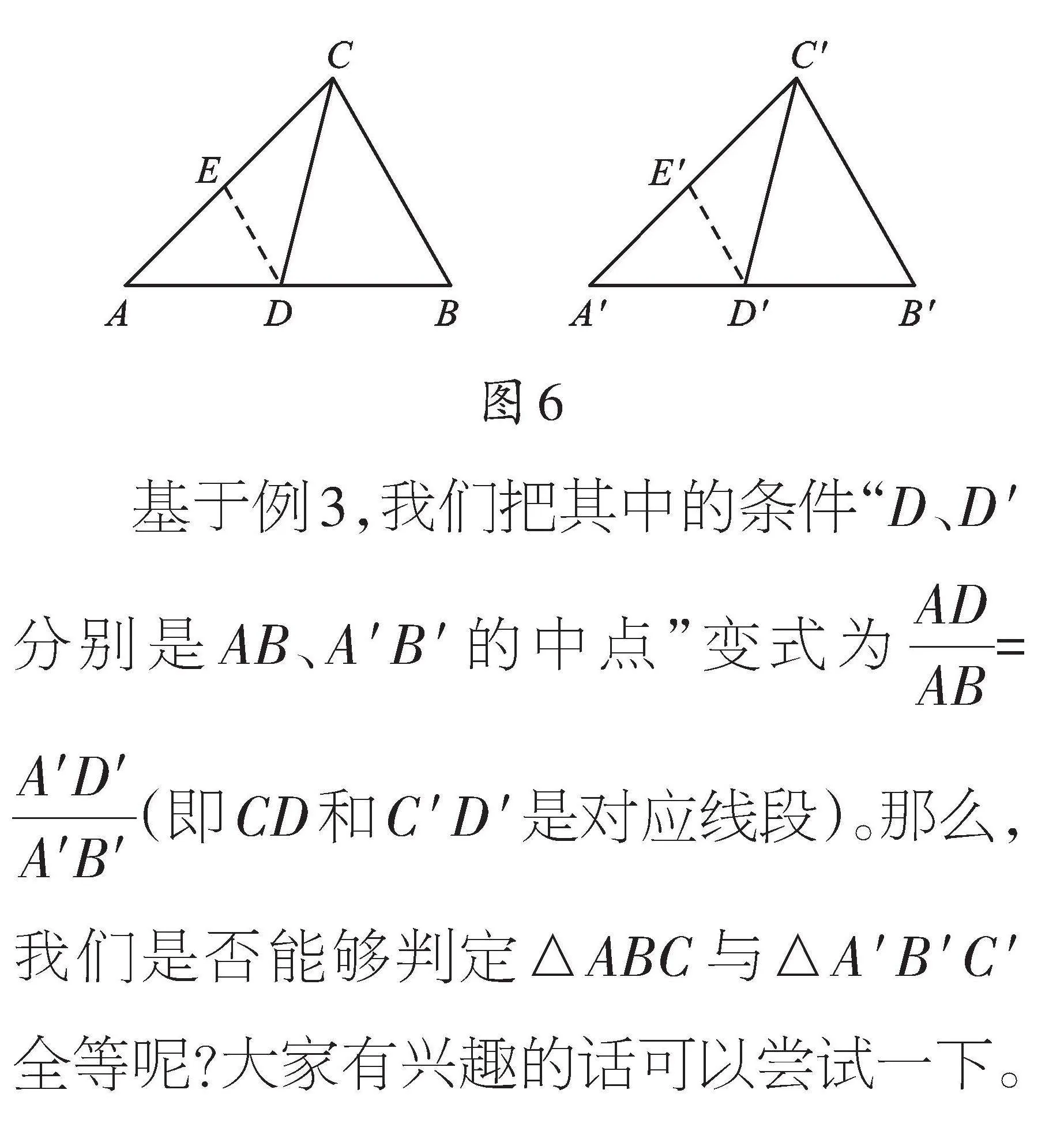
【解析】例3與例1類似，這個(gè)問題并不陌生，是我們在學(xué)習(xí)全等三角形時(shí)研究過的。如圖6，可以分別取AC、A′C′的中點(diǎn)E、E′，連接DE、D′E′。這樣就可以把AC=A′C′，BC=B′C′轉(zhuǎn)化為EC=E′C′，ED=E′D′，再結(jié)合CD=C′D′，就能先證明△CED≌△C′E′D′，得到∠ACD=∠A′C′D′。再證明△ACD≌△A′C′D′，得到AD=A′D′，AB=A′B′，這樣就可以證明△ABC≌△A′B′C′。

基于例3，我們把其中的條件“D、D′分別是AB、A′B′的中點(diǎn)”變式為[ADAB]=[A′D′A′B′]（即CD和C′D′是對應(yīng)線段）。那么，我們是否能夠判定△ABC與△A′B′C′全等呢？大家有興趣的話可以嘗試一下。

同學(xué)們，我們之前接觸較多的是推理兩條線段之間的相等關(guān)系，而現(xiàn)在需要解決的是四條線段之間的比例關(guān)系。這就需要我們在學(xué)習(xí)時(shí)厘清全等和相似的關(guān)系，全等是特殊的相似。一些證明三角形相似的問題，可以通過作平行線將相似的問題轉(zhuǎn)化為全等的問題來解決。但有一些經(jīng)典圖形模型，如“手拉手”“一線三等角”等模型，我們需要在具體的題目中進(jìn)行分解、感悟，既要心中有模，也不能唯模不變。我們需要努力提高解決綜合問題的能力，用變中不變、變中有序的眼光來看問題。

（作者單位：江蘇省南京市鼓樓區(qū)教師發(fā)展中心）