借力旋轉 探尋本質

旋轉是初中幾何圖形變化的一種基本方式。以旋轉為載體的圖形相似問題是命題的熱點和難點。這類問題具有一定的共性，即在旋轉過程中會隱藏諸多“不變”的關系。下面就通過一些例題，幫助同學們感受旋轉在圖形相似中的應用，體會以“不變”應萬“變”。

一、感受旋轉，建立模型

引例 如圖1，在△ABC與△ADE中，已知∠BAC=∠DAE。

（1）要使△ABC∽△ADE，還需要添加什么條件？

（2）連接BD和CE，當△ABC∽△ADE時，是否有其他相似的三角形？若有，請寫出對應邊的比例式。

【解析】（1）要使兩個三角形相似，在已有一組對應角相等的情況下，只需要再找到一組對應角相等或這對等角的兩條鄰邊對應成比例即可。可以添加∠B=∠D或∠C=∠E或[ABAD]=[ACAE]。（2）在△ABC∽△ADE相似的情況下，會有[ABAD]=[ACAE]，∠BAC=∠DAE。連接BD、CE后，由∠BAC=∠DAE，得∠BAD=∠CAE；由[ABAD]=[ACAE]，得[ABAC]=[ADAE]，此時，就有△ABD∽△ACE，對應邊會滿足[ABAC]=[ADAE]=[BDCE]。

【點評】本題中△ABC與△ADE有公共頂點A，可以看作將△ABC繞點A旋轉一定角度后，再放大形成△ADE，這類經過旋轉和相似變化得到的基本圖形稱為“旋轉相似模型”。連接兩個相似三角形的對應點B、D和C、E后，必然伴隨著第二次相似（△ABD∽△ACE），使得原本沒有聯系的兩條線段BD和CE與原三角形的邊對應成比例。

二、運用模型，感受規律

例1 如圖2，在Rt△OAB和Rt△OCD

中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，連接AC，交BD的延長線于點M，請計算[ACBD]的值及∠AMB的度數。

【解析】由題目中兩組相等的角，易知△OAB∽△OCD，由含30°角的直角三角形的特點可知[OCOD]=[OAOB]=[3]，而這組比例關系可以用于證明△COA∽△DOB，得到[ACBD]=[OCOD]=[3]，∠CAO=∠DBO，再由“8”字模型求得∠AMB=∠AOB=90°。

【點評】本題是“旋轉相似模型”的直接運用，Rt△OAB可以看作由Rt△OCD繞點O旋轉后放大得到的。第二組相似三角形也以點O為旋轉中心，通過兩邊成比例且夾角相等，證得△COA∽△DOB。

三、構造模型，培養思維

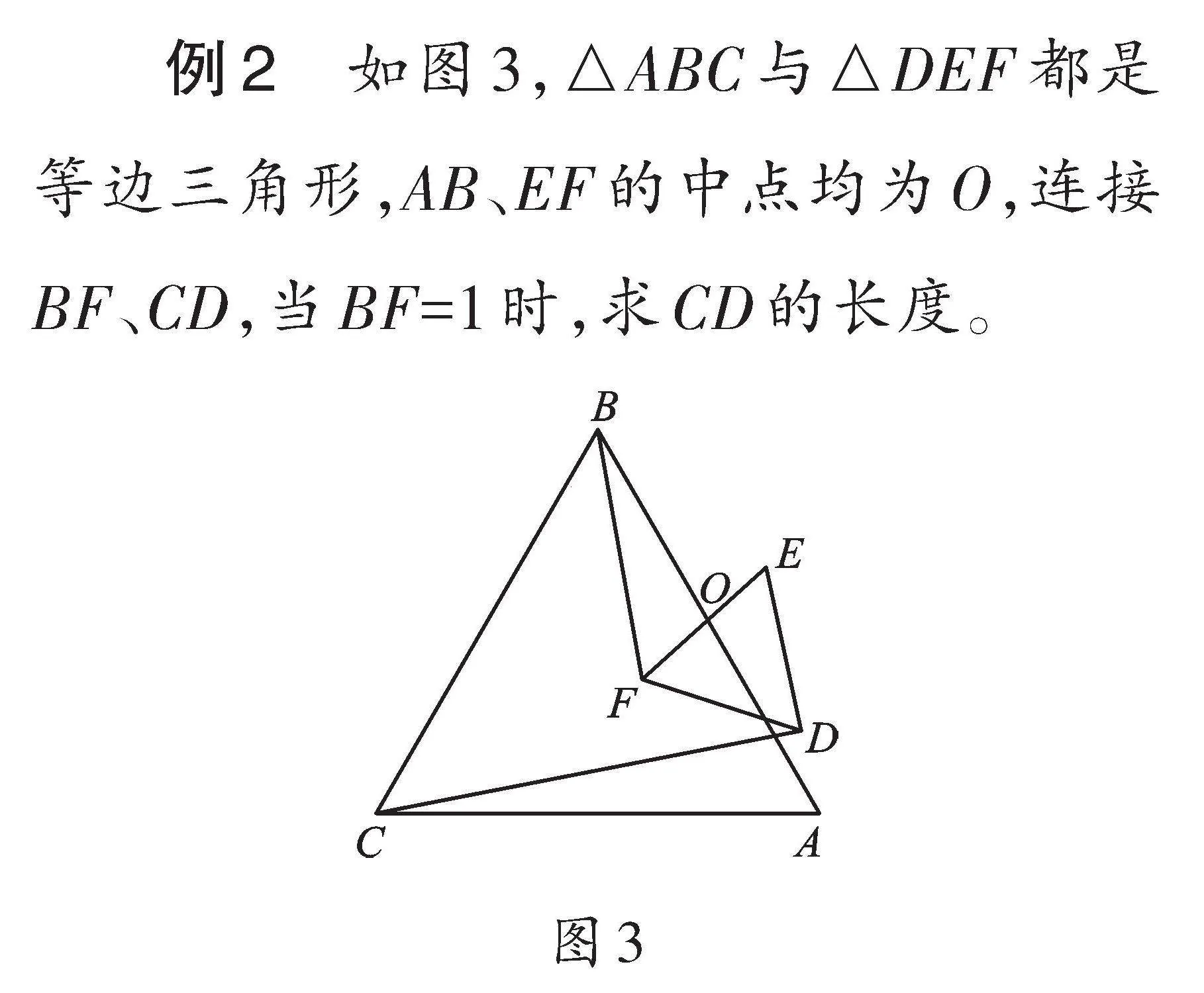
例2 如圖3，△ABC與△DEF都是等邊三角形，AB、EF的中點均為O，連接BF、CD，當BF=1時，求CD的長度。

【解析】我們通常會分別找出BF和CD所在的三角形，看其是否相似，從而得到BF與CD的比例關系。因為圖中沒有這樣的三角形，所以我們考慮添加輔助線構造能包含CD和BF的相似三角形。由等邊三角形的性質和中點，想到連接OC、OD（如圖4），這樣就能得到△BOC∽△DOF，所以有[OBOC]=[OFOD]=[33]，∠BOC=∠DOF，則∠BOF=∠COD，所以△BOF∽△COD。因此CD=[3]。

【點評】題中明顯相似的兩個等邊三角形并不具有“旋轉相似模型”的特征，但AB、EF的中點都是點O，所以我們可以將這兩個等邊三角形看作分別繞著一條邊的中點旋轉。Rt△BOC可以看作由Rt△FOD繞點O旋轉后放大得到的，因此，第二組相似△BOF∽△COD也伴隨出現，把本身沒有關聯的CD和BF聯系在相似三角形的對應邊上。

（作者單位：江蘇省南京市第二十九中學初中部）