以相似之手，解最值問題

相似是幾何中轉化線段與角的重要工具。將相似與函數、圓相結合，通過添加適當的輔助線，構造相似圖形基本模型，可以解決線段的最值問題。

例1 如圖1，在正方形ABCD中，AB=6，AE=[13]AB，點F在AD上運動（不與A、D重合），過點F作FG⊥EF交CD于點G，則DG的最大值為 。

【解析】由“一線三等角”模型易證△AEF∽△DFG。設AF=x，則DF=6-x。通過[AEDF]=[AFDG]，可得DG=[12]x（6-x）=[-12]（x-3）2

[+92]。∵0＜x＜6，∴當x=3時，DG取最大值[92]。

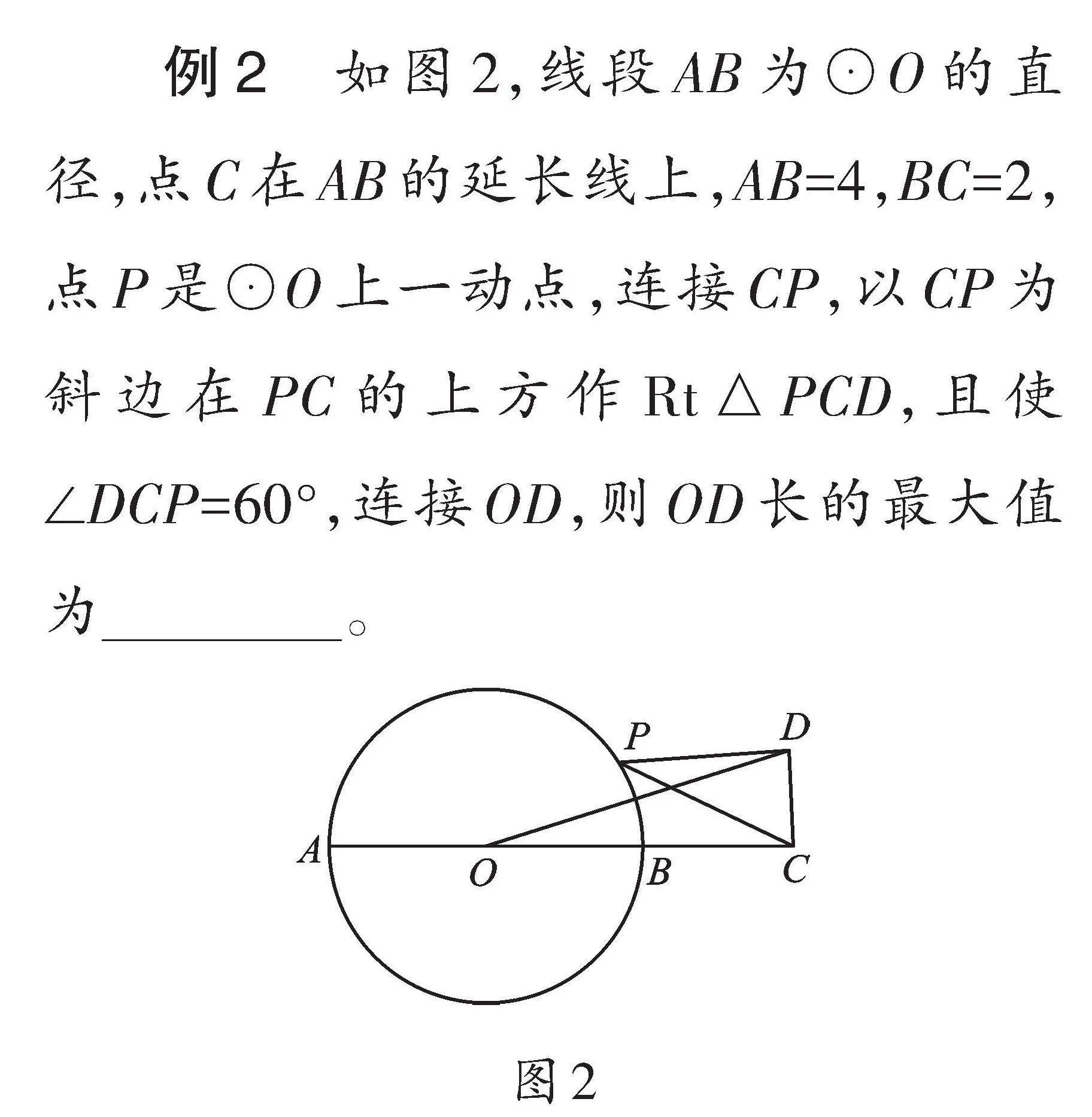
例2 如圖2，線段AB為⊙O的直徑，點C在AB的延長線上，AB=4，BC=2，點P是⊙O上一動點，連接CP，以CP為斜邊在PC的上方作Rt△PCD，且使∠DCP=60°，連接OD，則OD長的最大值為 。

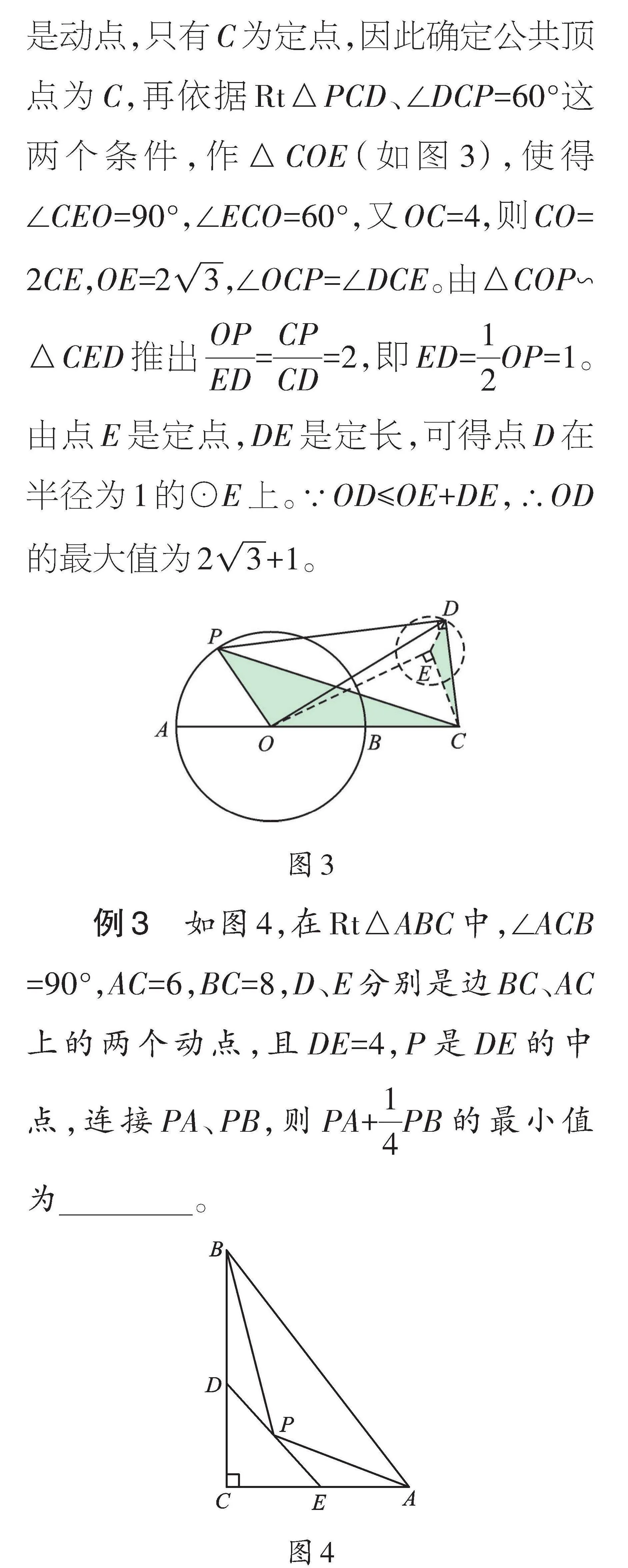
【解析】本題O為定點，所以需要尋求點D的運動軌跡。D、P兩點通過Rt△PCD、∠DCP=60°這兩個條件建立關系，屬于“主從聯動”問題，因此可以通過構造“手拉手”相似，確定點D的運動軌跡。而在Rt△PCD的三個頂點中，D、P都是動點，只有C為定點，因此確定公共頂點為C，再依據Rt△PCD、∠DCP=60°這兩個條件，作△COE（如圖3），使得∠CEO=90°，∠ECO=60°，又OC=4，則CO=2CE，OE=[23]，∠OCP=∠DCE。由△COP∽△CED推出[OPED]=[CPCD]=2，即ED=[12]OP=1。由點E是定點，DE是定長，可得點D在半徑為1的⊙E上。∵OD≤OE+DE，∴OD的最大值為[23]+1。

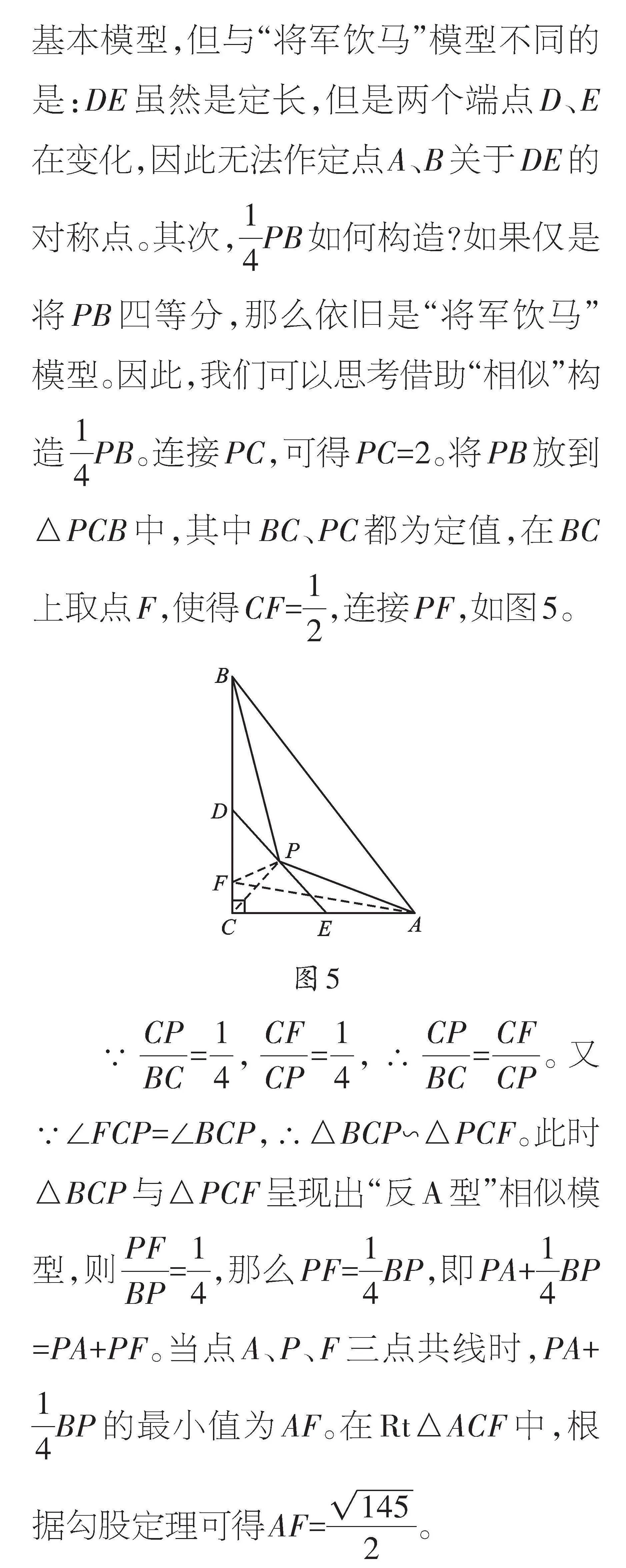
例3 如圖4，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，D、E分別是邊BC、AC上的兩個動點，且DE=4，P是DE的中點，連接PA、PB，則PA+[14]PB的最小值為 。

【解析】本題要求解兩條變化的線段之和的最小值，可能會想到“將軍飲馬”基本模型，但與“將軍飲馬”模型不同的是：DE雖然是定長，但是兩個端點D、E在變化，因此無法作定點A、B關于DE的對稱點。其次，[14]PB如何構造？如果僅是將PB四等分，那么依舊是“將軍飲馬”模型。因此，我們可以思考借助“相似”構造[14]PB。連接PC，可得PC=2。將PB放到△PCB中，其中BC、PC都為定值，在BC上取點F，使得CF=[12]，連接PF，如圖5。

∵[CPBC]=[14]，[CFCP]=[14]，∴[CPBC]=[CFCP]。又∵∠FCP=∠BCP，∴△BCP∽△PCF。此時△BCP與△PCF呈現出“反A型”相似模型，則[PFBP]=[14]，那么PF=[14]BP，即PA+[14]BP=PA+PF。當點A、P、F三點共線時，PA+[14]BP的最小值為AF。在Rt△ACF中，根據勾股定理可得AF=[1452]。

（作者單位：江蘇省南京市第二十九中學初中部）