走進生活，統計概率伴我行

為了解決某些實際問題，我們常經歷這樣的過程：提出問題→收集數據→整理、描述、分析數據→做出估計、推斷。而對于生活中的隨機問題，我們也常用概率模型幫助分析問題，做出估計、推斷、決策。

一、恰當選圖，直觀呈現

例1 空氣的成分（除去水汽、雜質等）是：氮氣約占78%，氧氣約占21%，其他微量氣體約占1%。要反映上述信息，宜采用的統計圖是（ ）。

A.條形統計圖

B.折線統計圖

C.扇形統計圖

D.頻數分布直方圖

【解析】扇形統計圖可以清楚地看出各統計項目占總體的百分比，所以用扇形統計圖。故選C。

【點評】我們要根據問題的需要選擇恰當的統計圖來解決問題。因此，了解各統計圖的特點是解題的關鍵。條形統計圖可以清楚地看出各統計項目的數據；折線統計圖能夠描述數據的變化過程和趨勢；頻數分布直方圖可以直觀、形象地反映樣本的分布規律，清楚地看出數據分布的總體趨勢。

二、統計分析，精準預測

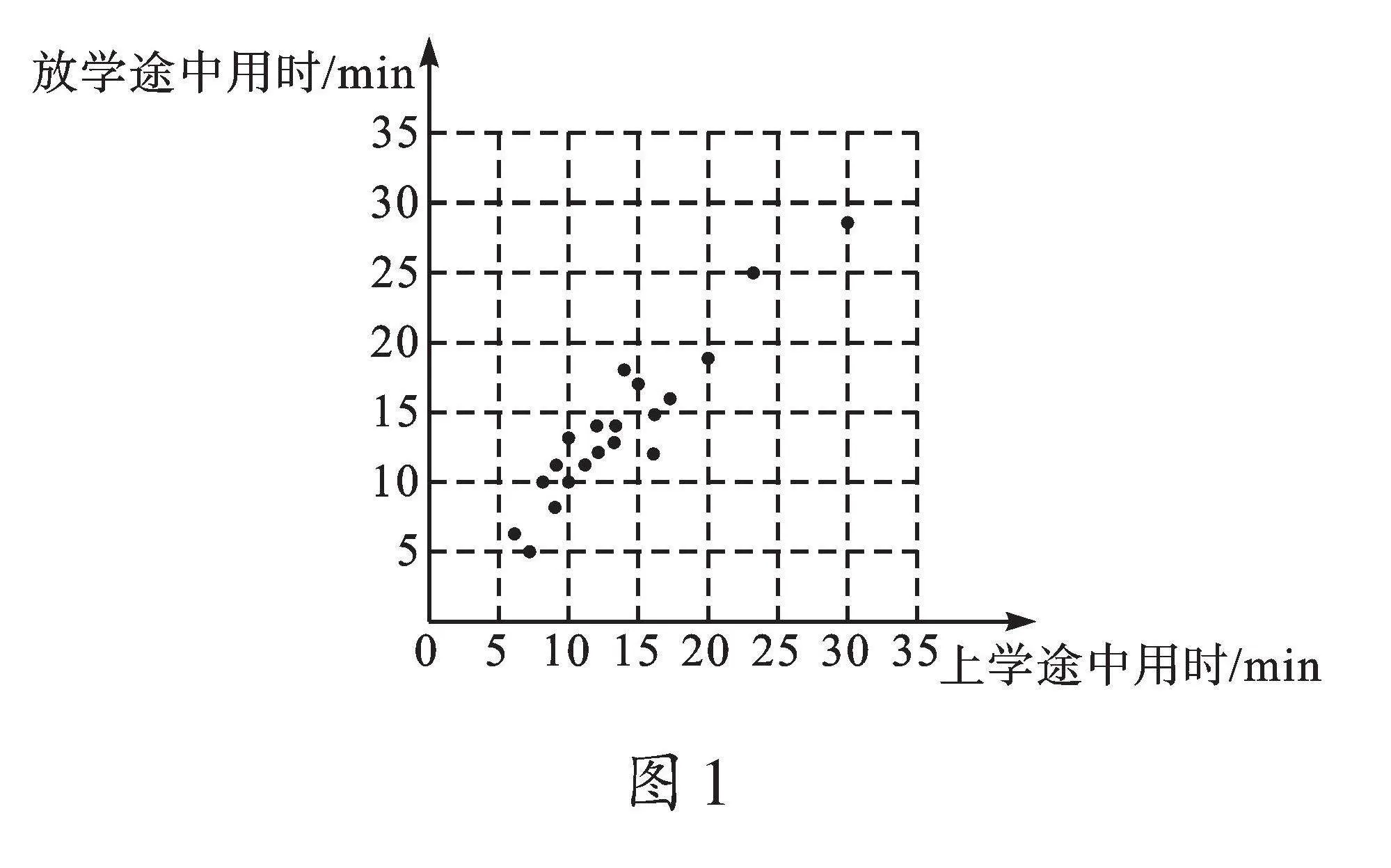
例2 為合理安排進、離校時間，學校調查小組對某一天八年級學生上學、放學途中的用時情況進行了調查。本次調查在八年級隨機抽取了20名學生，建立以上學途中用時為橫坐標、放學途中用時為縱坐標的平面直角坐標系，并根據調查結果畫出相應的點，如圖1所示：

（1）根據圖中信息，下列說法正確的是 （寫出所有正確說法的序號）。

①這20名學生上學途中用時都沒有超過30min；

②這20名學生上學途中用時在20min以內的人數超過一半；

③這20名學生放學途中用時最短為5min；

④這20名學生放學途中用時的中位數為15min。

（2）已知該校八年級共有400名學生，請估計八年級學生上學途中用時超過25min的人數。

（3）調查小組發現，圖中的點大致分布在一條直線附近，請直接寫出這條直線對應的函數表達式并說明意義。

【解析】（1）上學途中的用時情況，需要觀察圖中這些點的橫坐標。從圖上看，所有的點的橫坐標都小于等于30，①正確。要找上學途中用時在20min以內的人數，就要看這些點中橫坐標小于等于20的點有多少個，超過了一半，就是大于等于10名，②正確。這些點的縱坐標最小是5，所以放學途中用時最短的是5min，③正確。求放學途中用時的中位數，要從下往上數，找到第10個和第11個點，看它們對應的縱坐標，求出平均數即可，發現小于15，④錯誤。

（2）從抽取的樣本來看，橫坐標超過25的點只有1個，所以用樣本估計總體則有400×[120]=20，估計有20人。

（3）這條直線對應的函數表達式為y=x。實際意義是：每名學生上學、放學途中用時接近。

【點評】這是一個生活中的常見情境，跟我們的生活息息相關。解決此類問題的方法就是將生活問題數學化，建立平面直角坐標系，理解每個點的意義。

例3 某汽車評測機構對市面上多款新能源汽車的0～100km/h的加速時間和滿電續航里程進行了性能評測，評測結果繪制如圖2，每個點都對應一款新能源汽車的評測數據。

已知0～100km/h的加速時間的中位數是ms，滿電續航里程的中位數是nkm，相應的直線將平面分成了①②③④四個區域（直線不屬于任何區域），欲將最新上市的兩款新能源汽車的評測數據對應的點繪制到平面內，若以上兩組數據的中位數均保持不變，則這兩個點可能分別落在（ ）。

A.區域①② B.區域①③

C.區域①④ D.區域③④

【解析】這些點的橫坐標表示滿電續航里程，縱坐標表示0～100km/h的加速時間，要使得兩款新能源車的評測數據加進去后，滿電續航里程的中位數不變，則兩個數據應該位于直線n的左右兩側，使原先排在最中間的兩個點的位置不變。同樣的道理，要使得0～100km/h的加速時間的中位數不變，新加進去的兩個點的位置應分布在直線m的上下兩側，所以只有B選項符合。

【點評】這個生活問題本質上考查的是中位數的概念。研究中位數時，我們通常見到的都是具體的數據，而這里以散點圖的方式呈現。和例2一樣，我們同樣要理解每個點的橫坐標和縱坐標所代表的含義。這里雖然沒有具體數據，但是從點的位置分布的高低和左右情況可以看出數據的大小。

三、生活游戲，概率幫忙

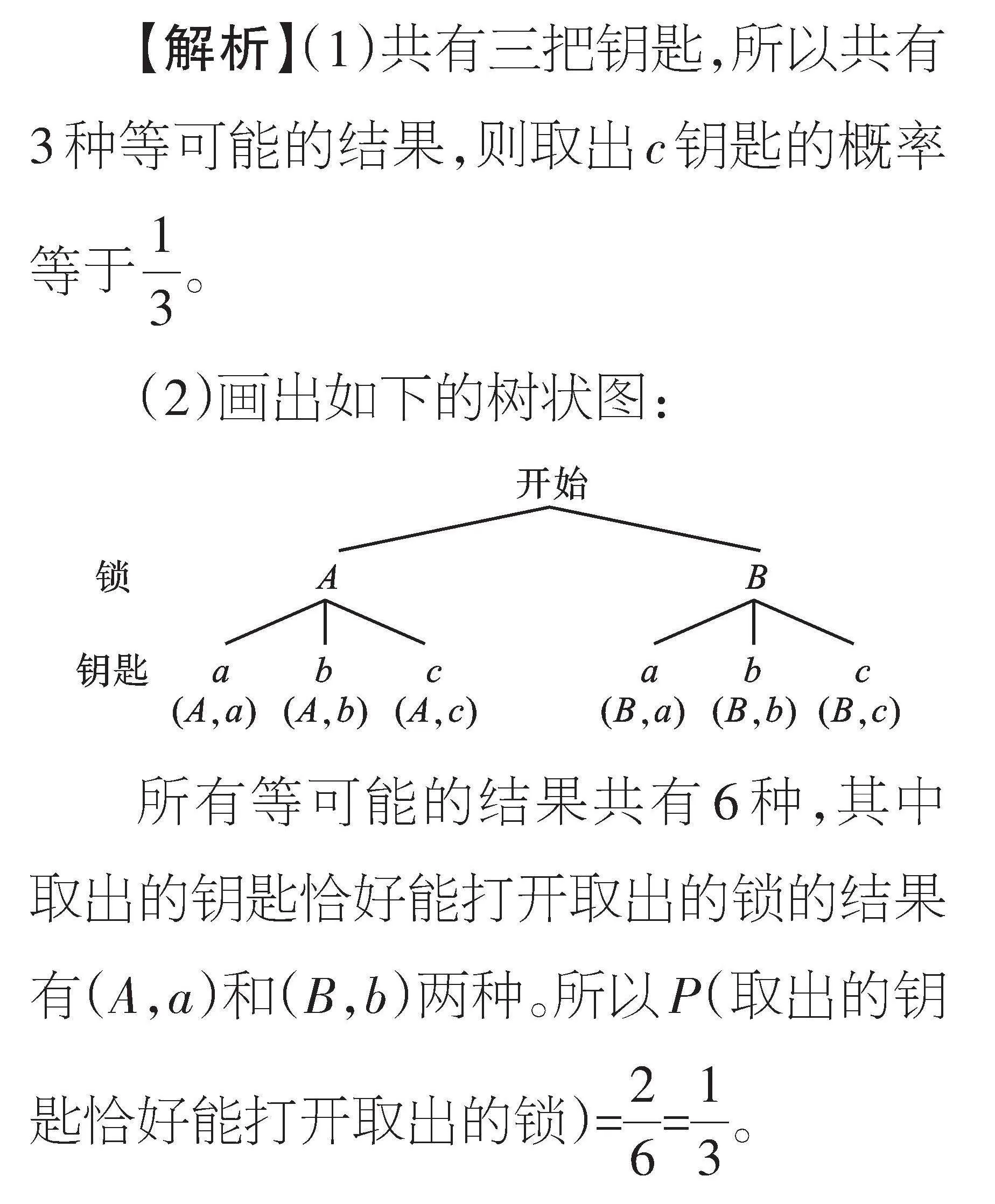
例4 有同型號的A、B兩把鎖和同型號的a、b、c三把鑰匙，其中a鑰匙只能打開A鎖，b鑰匙只能打開B鎖，c鑰匙不能打開這兩把鎖。

（1）從三把鑰匙中隨機取出一把鑰匙，取出c鑰匙的概率等于 ；

（2）從兩把鎖中隨機取出一把鎖，從三把鑰匙中隨機取出一把鑰匙，求取出的鑰匙恰好能打開取出的鎖的概率。

【解析】（1）共有三把鑰匙，所以共有3種等可能的結果，則取出c鑰匙的概率等于[13]。

（2）畫出如下的樹狀圖：

所有等可能的結果共有6種，其中取出的鑰匙恰好能打開取出的鎖的結果有（A，a）和（B，b）兩種。所以P（取出的鑰匙恰好能打開取出的鎖）=[26]=[13]。

【點評】本題考查的是根據概率公式求概率，可以用樹狀圖或者表格，不重復、不遺漏地列出所有等可能的結果。這里是兩步完成的事件，兩種方法均可。若是三步及以上完成的事件，只能用樹狀圖。分析問題時要關注問題是放回試驗，還是不放回試驗。本問題為不放回試驗。

（作者單位：江蘇省常州市鐘樓外國語學校）