基于2024年高考綜合改革適應性測試的數學備考策略研究

范明輝

２０２４年１月，第四批高考綜合改革省份組織了適應性測試“九省聯考”，試題由教育部教育考試院依據高校人才選拔要求和?普通高中數學課程標準（２０１７年版２０２０年修訂）?（以下簡稱課程標準）命制，可供依據課程標準教學、使用高考全國卷的省份參考借鑒．通過對比２０２１年舉行的“八省聯考”和同年的高考數學試題，可以發現高考試題中的許多新變化早就在２０２１年舉行的“八省聯考”試題中就釋放信號了．由此可見，２０２４年高考數學將如何變化，或許可以從此次適應性測試中明晰考查方向，助力數學教學，實現科學備考．

１ 高考綜合改革適應性測試的背景分析

２０２０年１０月，中共中央、國務院印發了?深化新時代教育評價改革總體方案?，方案指出要深化考試招生制度改革，改變相對固化的試題形式，增強試題的開放性，減少死記硬背和“機械刷題”現象．課程標準中也提出，在高考數學的命題中，要關注試卷的整體性，逐步減少選擇題、填空題的題量，適度增加試題的思維量，給學生充足的思考時間，關注內容與難度的分布、數學學科核心素養的比重與水平的分布，發揮高考數學的選拔功能．

據此，教育部相繼發起了“八省聯考”（２０２１年１月）、“四省聯考”（２０２３年２月）、“九省聯考”（２０２４年１月）共３次適應性測試，不斷調整試題考查內容、優化試卷結構，采用更加科學合理的賦分規則與試卷題量，有序推進各省高考數學改革．

２ 適應性測試數學試題分析

２.１ 試題結構分析

與２０２３年高考試卷相比，本次適應性測試試卷的多選題、填空題和解答題題量各減少了一道，同時３道多選題與５道解答題分值出現了較大的變化．多選題一道６分，部分選對的得部分分，然而這個得分標準比較模糊．一般而言，多選題正確選項的個數為２或３，不難推理，比較合理的賦分方式就是平均賦分：若正確選項的個數為２，則選對１個得３分，全部選對得６分，有錯選得０分;若正確選項的個數為３，則選對１個得２分，選對２個得４分，全部選對得６分，有錯選得０分．

多選題、解答題的分值以及賦分規則的變化能夠有效地增加數學試題的區分度，從而區分出在高中數學方面表現出不同發展水平的學生，并拉開不同程度學生之間的差距．這種變化有利于發揮數學試題對人才的選拔功能．

２.２ 逐題多維度細目表

本次適應性測試的一個明顯變化就是題量減少了，這有利于考生有較為充足的時間來深入分析每一道試題，認真思考，從容作答．如此一來，可能會出現兩種情形：

１）要盡可能多地考查高中數學知識，那么就要在知識的交會處命題，這樣每一道試題就會涉及多個高中數學知識點，試題的綜合性便會增強，試題的難度自然就不會低;

２）重點考查高中數學核心知識內容，試題形式和內容靈活多變，不再固化，押題、猜題等應試手段都將是“無頭蒼蠅”．

無論是上述哪種情形，考生通過死記硬背和“機械刷題”就想在高考中取得成功將會成為天方夜譚，考生必須夯實數學基礎、理解數學思想、掌握數學方法、重視數學思維、把握數學本質，才能夠較好地應對新高考，而這正好能夠達到高考數學改革的目的，成功地選拔出數學優秀人才．

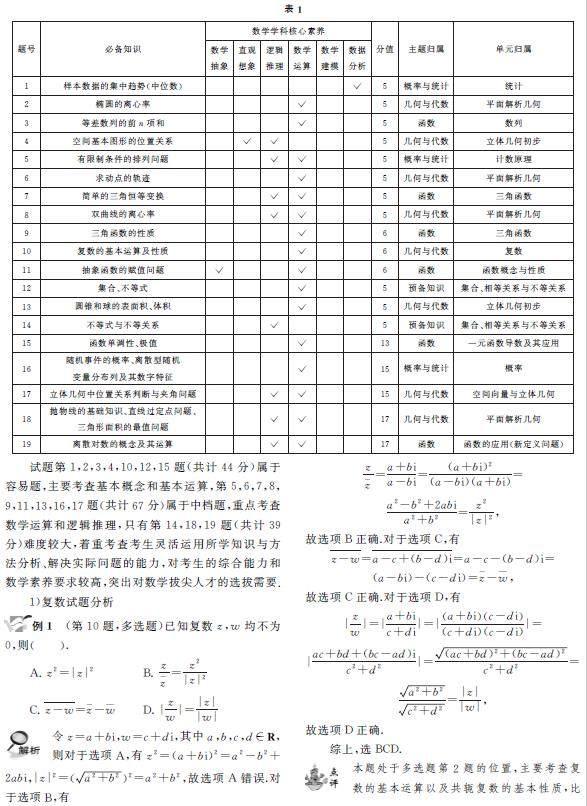
表１是“九省聯考”試題逐題多維度細目表．

２.３ 試題考查內容分析

通過表１不難發現，本次適應性測試對高中數學知識的考查并不是“面面俱到”，而是圍繞核心，突出重點．試題圍繞“預備知識”“函數”“幾何與代數”“概率與統計”等主題內容，突出對“基礎知識”“基本技能”“基本方法”的考查．

３ 高考數學備考策略

３.１ 夯實基礎知識，厘清來龍去脈

在本次適應性測試中，考查的高中數學知識內容是有側重點的，試卷題量減少很大程度上會導致備考方向不明確，不清楚高考會考哪些知識點．因此，考生在平時的學習和備考中要全面掌握高中課本中的全部知識點，特別是要非常熟練教材中的概念、公式、定理，不能存在任何知識盲區，不僅如此，還要從“知其然”到“知其所以然”，再到“知何由以知其所以然”．

另外，本次適應性測試的解答題中沒有考查“數列”和“三角函數”，但這并不表示２０２４年高考或未來的高考不會考查這兩塊內容，所以考生一定要做到“全面撒網、重點捕撈”．

３.２ 重視教材內容，挖掘習題功能

在上述試題分析內容中，多處提到了試題的“源”來自于課本的例題或習題，因此無論是教師還是學生都要在平時的學習過程中重視教材內容．學生至少要將課本上的例題、習題全部做一遍，定理、公式要會推導．教師還要在此基礎上對教材上的題目進行變式研究，挖掘習題的背景和功能，進行適當拓展．例如，在人教A 版高中數學必修第一冊第２５６頁第２６題介紹了“泰勒公式”，雖然這是大學數學的內容，但是它是許多高考試題的命題背景．教師可以結合高考題或模考題中出現的內容，提煉泰勒公式中的一些常用不等式結論，幫助學生掌握近幾年比較熱門的“比較大小”問題的不等式放縮方法．

３.３ 掌握思想方法，提升學習能力

２０２３年新高考Ⅰ卷中的導數解答題前移至解答題第三題，適應性測試中前移至解答題第一題，這無疑是在告訴大家，改革后的高考壓軸題不會進行題型固定，任何一個板塊的內容都可能成為壓軸題，導數題也可能變成“送分題”．因此，學生不應再抱有“押題、猜題”的想法，要認真抓好最基本的思想和方法．此外，適應性測試的壓軸題出現了“新定義”問題，涉及“初等數論”的內容，這導致近期許多的模考題出現了“群模亂舞”現象．大家都在恐慌，是不是要開始搞競賽研究了？ 競賽生是不是要占優勢了？ 其實并不需要擔心，為保證考試的公平性，高考的命題背景不會偏向某一類人，即便是新定義問題，大家所面對的背景都是一樣不熟悉的．教育部的這次適應性測試所釋放的信號是利用新定義問題來區分和選拔數學拔尖人才，考查學生面對新材料時的閱讀理解能力和面對新問題時分析和解決問題的能力，強調數學的應用性．處理這些新定義問題的方法還是平時在課堂上、教材中學到的那些基本的數學思想方法．

分析近幾年的高考試題和適應性測試試題可以發現，命題突出的是函數、代數與幾何、概率與統計三大主題的內容，反映的是數學本質的核心概念、主要結論、通性通法、數學應用和實際應用，關注的是學生的數學思維品質和會學數學的能力．

３.４ 訓練思維方式，進行差異教學

基于本次適應性測試以及以往的一些重大考試，可以發現高考數學試題的材料信息更加豐富、命題背景更加新穎、解題方法更加多樣．這就要求學生在平時的學習和訓練中要注重思維方式，多角度進行思考、探究．以第１８題為例，部分學生處理第（１）問就已經很吃力了，對于第（２）問，常規運算相當煩瑣，幾何轉化思維難度大．出現這種情況是因為平時在處理解析幾何問題時，很多學生一拿到題目就開始“聯立”，沒有進行多角度的思維訓練，教師沒有進行差異化的個別輔導教學，導致學生很難突破解析幾何難點．

在今后的高考數學中，想取得高分是一件比較困難的事情，對于不同能力的學生，要實行差異化教學．在數學方面具備較強天賦的學生，可以多思考、探究一些學習和生活相結合的實際問題（如數學建模問題），包括對問題的數學抽象、符號理解、邏輯推理、數學運算、數學表達等，借此來訓練數學思維方式和問題解決能力．而對于基礎較為薄弱的學生，如果真正理解了教材內容，掌握了基礎知識、基本技能和基本思想方法，在高考中拿到基本分是沒有問題的．