熒光油膜速度場的自適應快速光流解法

蔡章博，張征宇，余皓，占書恒

1.西南科技大學 信息工程學院，綿陽 621000

2.中國空氣動力研究與發展中心 高速空氣動力研究所，綿陽 621000

降低摩阻意味著飛行器的油耗下降、航程增加［1-3］。基于熒光油膜的全局摩阻直接測量法，具有測量設備簡單（僅需紫外激發光源、相機與鏡頭）、空間分辨率高、對模型物面無特殊要求等優點，已成為研究的熱點和發展趨勢［4-6］。該法是基于油流法［5］，在油膜中加入熒光分子，通過熒光油膜控制方程，描述熒光油膜（受紫外光激發的發光成像）灰度與其運動速度的關系，推導出基于熒光油膜的摩阻測量方程［6］。因其測量方程與光流方程［7］具有相似的形式，因此，采用光流法解算風洞試驗中模型表面熒光油膜運動的時序圖像，即可獲得試驗模型的近壁面流動結構，為掌握試驗模型壁面發生流動分離的位置、分離方式與特點、漩渦形成機制等提供重要的研究數據。

自1981 年Horn和Schunck［7］提出了Horn-Schunck（HS）光流法后，Wildes等［8］引入流體力學原理率先將其用于云運動估計，2008 年Liu和Shen［9］建立了光流法和流體流動之間的數學聯系。2015年，Zhong等［10］重建了機翼連接處的全局摩擦力拓撲結構；Liu等［11］研究表明，光流法較粒子圖像測速法可獲取更密集的流體運動速度場。2016、2017年，黃湛等［12］、王鵬等［13］先后采用變分迭代方法求解表面摩阻分布，驗證了基于熒光油膜的全局表面摩阻測量技術的有效性。2019年，鄒易峰等［4］通過添加人工網格線利用離散匹配，實現了模型振動與油膜運動的解耦，提高了測量精度。

但是上述光流法的數值計算中，都采用了類雅克比的矩陣分割迭代形式，存在計算復雜度高、收斂速度慢、耗時長等問題［14］，故現有光流法尚難在生產型風洞的熒光油膜試驗現場實時測量并顯示模型壁面流動過程，降低了工程應用的價值。

因此，高效的光流法對于基于熒光油膜的全局摩阻實時測量至關重要。尤其是隨著高分辨率（可達2 500 萬～6 500 萬像素）的高速工業相機在熒光油膜風洞試驗中的應用，使用現有光流法處理2 GB/s 的海量熒光油膜時序圖像，需要在試驗結束后花1～2 h 才能獲得一次試驗的精細測量結果。

為此，本文提出熒光油膜速度場的空間自適應快速光流解法，一方面在數值計算方式上，通過構造共軛迭代式，較現有光流法的雅可比矩陣分割迭代式有更高的計算效率；另一方面，借鑒金字塔思想，對熒光油膜圖像進行空間的灰度梯度與速度場自適應降/升采樣，有效降低計算的復雜度，進一步提升熒光油膜速度場的解算速度。

1 光流法的類雅可比迭代式

當前風 洞試驗 中常采 用Liu等［15-17］基于Horn-Schunck 光流所改進的光流法，該方法追求一個全局能量泛函最小化的解，公式為

式中：Ix、Iy、It分別為圖像灰度沿x、y 方向空間域及時域上的梯度信息；α 為全局平滑參數，該值越大代表追求更平滑的解，即顆粒度更精細的速度場；(u，v)為給定坐標點(x，y)的速度向量。通過歐拉-拉格朗日方程最小化求解可得

式中：Δ 為拉普拉斯算子，通常以有限差分形式近似Δu(x，y)=n((x，y)-u(x，y))；()為給定點坐標下n 鄰域內(u，v)的加權值［7］，代入式（2）可得

后續為便于構造共軛迭代式，此處定義一個系數a ≈α 且a ≤α。當a=α時，經由式（3）構造的現有光流迭代式為

式（4）為一種類雅可比的矩陣分割迭代形式，收斂誤差為

式中：eu、ev分別為(u，v)當前步和上一步的殘差。

現有光流法在迭代過程中，會運用到迭代點局部鄰域的信息，其中灰度梯度大的像素點在式（4）中的加權值高，即局部鄰域施加的影響大。較共軛迭代式，該迭代方式所需存儲量大、收斂速度慢得多［18］，其收斂速度與迭代矩陣的譜半徑相關，尤其是隨著高分辨率高速工業相機應用，在高分辨率條件下追求更為平滑的速度場時，相鄰像素點圖像灰度梯度信息變化趨于平緩，迭代矩陣譜半徑增大，進而導致收斂耗時增加。

2 空間自適應快速光流解法

2.1 共軛迭代式推導

考慮到油膜速度場中速度梯度大的像素點其灰度梯度大，為此，約定(u，v)等于鄰域內的速度最大值(um，vm)，有

鑒于共軛梯度法所需存儲量小，具有步收斂性、穩定性高的優點［18］，為此，借鑒局部光流法中“鄰域內速度具有相關性”的思想［19］有

代入式（6），有

式中：λ 的大小反映了鄰域內的平滑程度，為接近0 的正值，通常取0.001～0.010。故式（3）可化為

化為Ax=b 形式，即

顯然A 為一個對稱正定矩陣，必然存在共軛向量ri滿足

設rk+1=rk-αkApk，其中，pk為殘差方向的單位向量；αk為步長。Schmidt 正交化可得

為了求解αk，構造如式（14）的二次型：

式中：x=(uk，vk)T。式（14）與式（10）同解，將f (xk+akpk)記作g(ak)，令g′(ak)=0 可得

至此，求解光流方程的共軛迭代式為

2.2 油膜圖像的空間自適應采樣

為提高光流法在大位移下的精度，有學者提供了網格匹配［21］、金字塔采樣［22-24］的思路。本文借鑒金字塔思想，通過對熒光油膜圖像進行空間的灰度梯度與速度場自適應降/升采樣，以有效提高大運動估計的精度并降低計算的復雜度。為此，本文提出了基于八鄰域的空間尺度的灰度梯度與速度場自適應降/升采樣方法。

如圖1 所示，沿(u，v)方向將給定圖像的灰度梯度(Iu，Iv)矩陣按照3×3 大小進行分塊，邊界未能整除分塊的部分以0 填充對齊，對于給定的3×3 圖像塊，通過自適應降采樣后得到1 個像素，其灰度梯度為如此，即可解算得到空間降采樣層的速度場(u′，v′)，再借助原八鄰域梯度信息對(u′，v′)升采樣恢復到原有分辨率下的(u，v)。

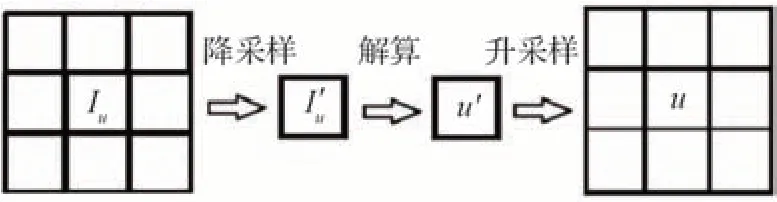
圖1 自適應采樣示意圖Fig.1 Process of proposed adaptive sampling

2.2.1 基于八鄰域的灰度梯度自適應降采樣

對于給定的熒光油膜圖像上3×3 圖像塊，為了保留八鄰域內權重最大圖像灰度梯度信息，可將其灰度梯度分為兩類，即

式中：Iumax、Iumin分別為原始圖 像(x，y)的n鄰域內u 方向的梯度最大、最小值；v 方向的梯度計算同理。降采樣示意圖如圖2 所示，在該八鄰域內梯度高于均值的點更多，滿足式（14）中取Iumax的條件，則取該區域內的梯度最高值12 作為采樣值。

圖2 灰度梯度自適應降采樣示例Fig.2 Example of proposed gray-gradient down-sampling

較傳統的雙線性插值的降采樣方法，本文方法得到灰度梯度矩陣會保留灰度梯度顯著區域的信息。

2.2.2 基于八鄰域的速度場自適應升采樣

通過共軛光流計算，得到灰度梯度自適應降采樣圖像的速度場。在后續計算中需要將速度場恢復到原圖像空間分辨率。鑒于傳統的雙線性插值方法難以在空間上升采樣后保留具有突變特征的速度場，為此，提出八鄰域的速度場自適應升采樣法，通過原有梯度信息對應恢復鄰域內速度向量，計算公式為

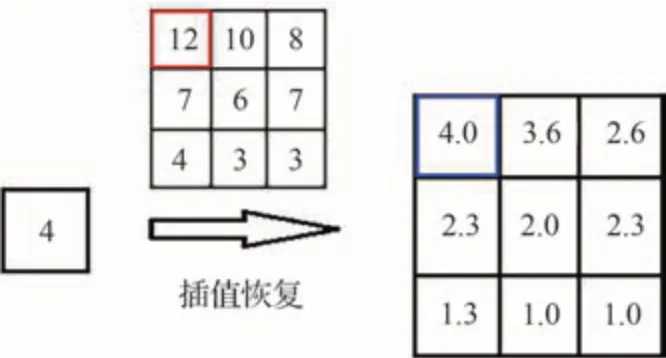
圖3 速度場八鄰域恢復示例Fig.3 Example of proposed velocity up-sampling

考慮到油膜速度場中速度梯度大的像素點其灰度梯度大，按照局部光流法理論用u、v 代替后，既減少了速度矩陣的存儲量和硬件線程同步耗時，又能采用共軛迭代法提升解算效率，快速得到表達大流動結構的速度場初值。再將速度場初值按照其八鄰域內點中灰度梯度分布插值，得到原圖空間分辨率速度場初值，再進行全局速度場優化，即可準確捕捉到精細的流動結構，有效提高熒光油膜速度場的解算速度。

2.3 算法流程

本文算法全部流程如圖4 所示，兩幀時序熒光油膜圖像分別對應圖像Pt、Pt+1。

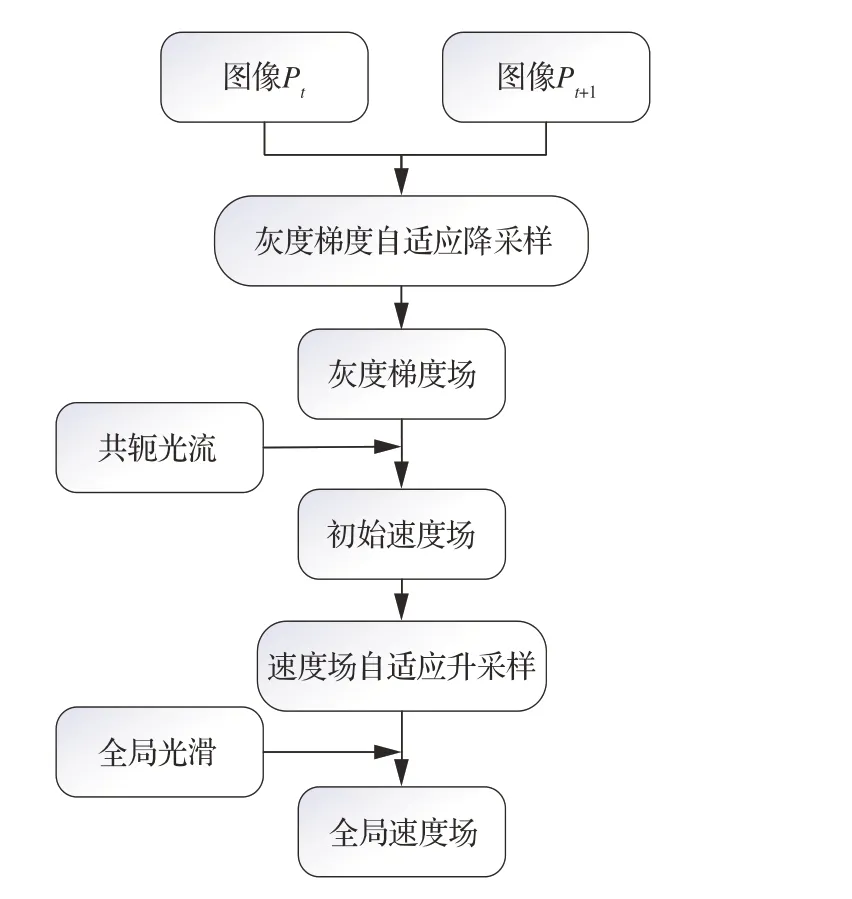
圖4 本文方法流程Fig.4 Process of proposed method

3 仿真實驗與分析

3.1 Ossen 渦對實驗

參照文獻［4，6］設計仿真實驗，利用圖5（a）、圖5（b）所示的熒光油膜模擬圖像表征給定的速度場為

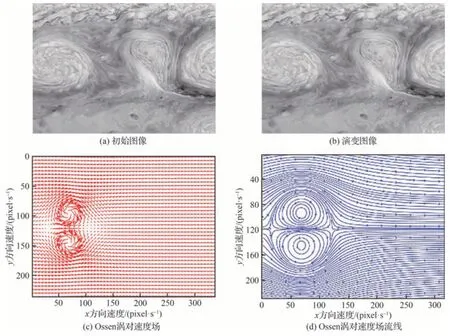
圖5 熒光油膜仿真圖像及Ossen 渦對速度場Fig.5 Fluorescent oil film simulation images and Ossen vortex pair velocity field

式中：Γ 為渦核強度，本實驗設定為5 000 pixel2/s；r0=30 pixel；u=10 pixel/s。在Ossen 渦對速 度場上再疊加一個勻速速度場，式（20）速度場疊加效果如圖5（c）所示，對圖5（a）利用雙線性插值，在演化步長為0.000 1 s 的條件下演化1 000步，取間隔0.1 s 后演化至5（b）所示熒光油膜模擬圖。

為驗證本文算法準確性，對上述流場下的演變圖像進行測試，限定迭代次數為300 進行對比實驗，為了扣除邊界條件對迭代計算的影響，忽略邊界像素點（x<20 pixel，x>200 pixel）的結果，得到的仿真實驗結果如圖6 所示。如表1 所示，本文方法計算的誤差更小，相比于文獻［4］方法最大誤差減小了2.3%，平均誤差減小1.4%。從圖6 也可看出本文方法較現有方法與理論曲線更為貼合，在一些速度變化較為平緩的區域本文方法效果更好。

表1 迭代300 次沿渦對分布的速度相對誤差Table 1 Average errors distributing along vortex pair under 300 iterations

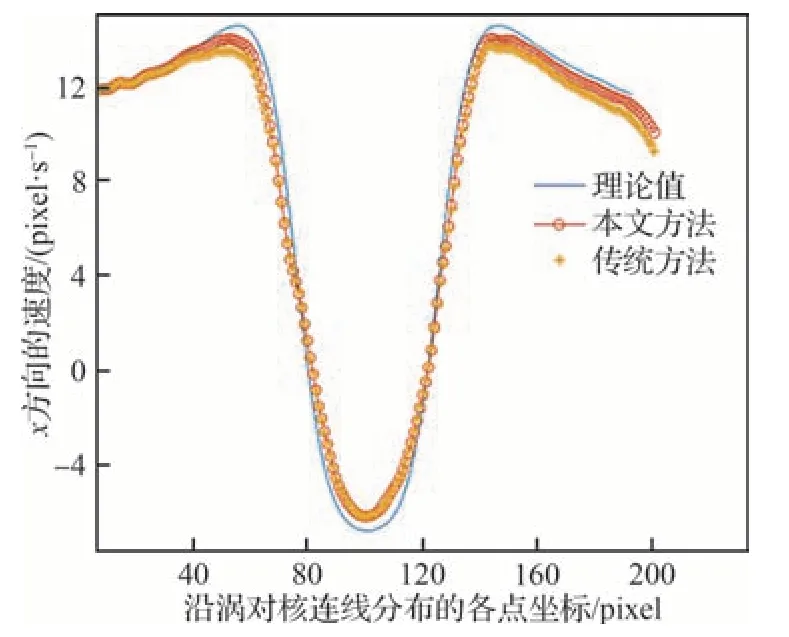
圖6 不同方法沿Ossen 渦對分布的測量速度Fig.6 Estimated velocities distributing along vortex cores under various methods

3.2 壁面射流實驗

參照文獻［25］選取2 張壁面射流圖像模擬流體油膜運動進行仿真實驗，為方便觀察，論文圖像在實驗圖像基礎上做了灰度拉伸（見圖7）。為驗證比較收斂速度，統計文獻［25］方法收斂到給定誤差限的迭代次數。壁面射流實驗共設定了3 個誤差 限：1.0×10-6、5.0×10-7、1.0×10-7，統計了不同方法收斂到誤差限所需迭代次數及所用時間。統計結果如表2 所示。

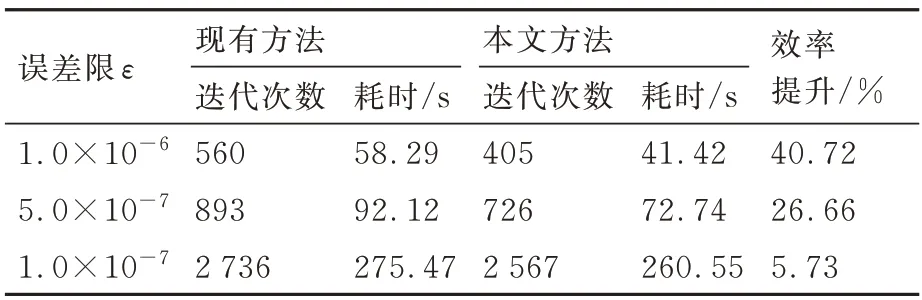
表2 壁面射流試驗在不同誤差限下收斂的迭代次數Table 2 Iterations to convergence with various error limits in wall-jet experiment

圖7 壁面射流圖像Fig.7 Images of wall-jet

可以看出在誤差限1.0×10-6、5.0×10-7的標準下，以耗時為例，本文方法效率分別提升了40.72%、26.66%。在1.0×10-7的誤差限下效率提升了5.73%，這是由于后續全局優化的解算性質，隨著迭代次數提高，整體的收斂速度放緩。如圖8 所示，在相同的全局收斂誤差限下，本文方法解得的流場特性會更加明顯。

圖8 同誤差限下實驗結果對比Fig.8 Comparison of results with same error limit

4 風洞試驗

4.1 某機翼表面熒光油膜風洞試驗

以某大展弦比靜彈性試驗機翼為對象，在2.4 m 跨聲速式風洞中開展驗證試驗（馬赫數Ma=0.82），相機分辨率為2 352 pixel×1 728 pixel，曝光時間為16 ms，鏡頭焦距為35 mm，采集幀率60 Hz，最終解算油膜速度場分辨率為2 000 pixel×1 200 pixel，采用本文算法處理該試驗采集的時序圖像，以便與文獻［4］的方法進行對比。

模型迎角α=0°時，試驗采集相鄰兩幀圖像如圖9（a）、圖9（b）所示，本文求解到的油膜運動速度場，通過視頻測量技術［26-27］可得到速度的標準單位（m/s），如圖9（c）所示。

圖9 機翼試驗圖像及解算結果Fig.9 Images and estimated result of wing test

由表3 可知，在誤差限為1.0×10-6、5.0×10-7、1.0×10-7的標準下，以耗時為例，本文方法效率分別提升了103.25%、53.66%、26.17%。

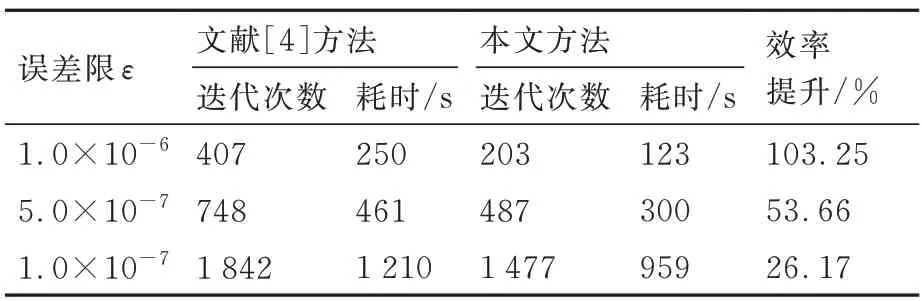
表3 機翼表面熒光油膜試驗在不同誤差限下收斂的迭代次數（α=0°）Table 3 Iterations to convergence with various error limits in fluorescent oil film test on wing surface（α=0°）

模型迎角α=10°時，取試驗采集相鄰兩幀圖像（見圖10（a）、圖10（b）），誤差限為1.0×10-7標準下求得的摩擦應力線圖譜如10（c）所示，以圖中矩形區域為例，著重與文獻［4］對應結果進行比較，其油流分離現象一致，本文方法解算效率提升26.17%。相比于傳統油流試驗圖像，本文方法得到了更豐富、清晰的流動細節。該試驗表明本文方法適用于曲面試驗模型。與文獻［4］中算法效率比較如表4 所示，在誤差限為1.0×10-6、5.0×10-7、1.0×10-7的標準下，以耗時為例，本文算法效率分別提升了9.76%、69.47%、19.89%。

表4 機翼表面熒光油膜試驗在不同誤差限下收斂的迭代次數（α=10°）Table 4 Iterations to convergence with various error limits in fluorescent oil film test on wing surface（α=10°）

圖10 機翼試驗圖像及解算結果Fig.10 Images and estimated result of wing experiment

4.2 平板上圓柱繞流油流試驗

在中國空氣動力研究與發展中心（CARDC）的0.6 m 連續式風洞中開展了“平板上的圓柱繞流油流”試驗（Ma=0.6）。圖11（a）中所示為試驗所用平板，紅色區域為熒光油膜，圖11（b）、圖11（c）為相鄰兩幀平板上圓柱繞流引起的油膜運動圖像，相機分辨率為5 120 pixel × 5 120 pixel，曝光時間為12.5 ms，鏡頭焦距為30 mm，采集頻率80 Hz，解算油膜速度場分辨率為1 200 pixel×780 pixel。

圖11 平板試驗圖像及解算結果Fig.11 Images and estimated result of flat plate experiment

如圖11（d）所示，當平板上的來流遇到圓柱障礙時，平板上圓柱附近的壁面邊界層速度開始下降、渦量開始增加，隨著渦量的增加，邊界層發生流動分離、不斷卷起形成漩渦并試圖脫離壁面時與來流相互作用，形成如圖11（d）、圖11（e）所示分離線，當漩渦前進一段距離再附時，將出現如圖11（d）、圖11（e）所示繞流附著線，其中圖11（e）所示分離點S1、S2，附著點A1 對應圖11（d）所標記點。以來流方向視角觀察氣流在S1 處發生分離時，邊界層氣流如圖11（e）所示由S1 流動至附著點A1，經過A1 的壁面氣流按圖示方式向前流動并經過S2。試驗結果與文獻［16］試驗測得流動現象相似，表明本文算法不僅能正確解算風洞試驗中油流路徑，而且提供了清晰的摩擦力線圖譜。

5 結論

推導了構造共軛迭代式，創建迭代效率更高的共軛光流法，將解得速度場作為初值有效提高后續全局優化效率。對熒光油膜圖像進行空間尺度的灰度梯度與速度場自適應降/升采樣，進一步提升高了熒光油膜速度場解算速度。

1）Oseen 渦對的熒光油膜路徑速度場仿真試驗結果表明：本文方法在計算結果在相同迭代次數下相比現有方法收斂效果更好，限定迭代300 次的情況下，比現有方法最大誤差減小了2.3%，平均誤差減小1.4%。壁面射流仿真試驗結果進一步表明，在同誤差限下本文方法解算出來的流場特征更為清晰。

2）風洞試驗中，本文方法不僅測得了正確流動現象，并且給出了清晰的摩擦力線圖譜，在誤差限較高標準下相較于文獻［4］方法，計算效率提升了26.17%。試驗結果證明本文方法相較于現有方法優勢明顯，工程應用價值大。