揭示2023年上海卷第21題本質
胡曉潔


1 題目:2023年上海卷第21題
已知f(x)=ln x,取點(a1,f(a1))過其作曲線y=f(x)的切線交y軸于點(0,a2),取點(a2,f(a2))過其作曲線y=f(x)的切線交y軸于點(0,a3),若an≤0則停止,以此類推,得到數列{an}.
(1)若正整數m≥2,證明:am=ln am-1-1;
(2)[JP3]若正整數m≥2,試比較am與am-1-2的大小;
(3)若正整數k≥3,是否存在k使得a1,a2,……,ak依次成等差數列?若存在,求出k的所有取值;若不存在,試說明理由.
2 分析與思維導圖
2.1 思維分析
本題從導數與數列的綜合運用出發,考查學生求切線方程、構造函數證明不等式、等差數列性質的應用以及方程有解問題的解決能力,體現了數學抽象、邏輯推理、數學運算等核心素養.本題的題干是由函數圖象的切線與y軸相交,交點的縱坐標經過遞推得到一個數列.遞推的過程和利用牛頓法求方程的解類似.數列在題目中更多是起到背景和提示作用,[JP3]本質上還是解決函數與導數的問題.本題作為上海卷的壓軸題,有較大的思維量,突出考查了數學抽象和邏輯推理核心素養.
第(1)問證明數列的遞推關系,本質上考查求函數的切線方程,要求學生理解題目中的遞推關系.本題對學生在給定情境下分析數學問題的能力有較高的要求.
第(2)問比較大小,常用辦法是將要比較的對象化成同一變量后作差.結合第(1)問的結論,可以發現本質上是考查常用不等式ln x≤x-1(ex≥x+1)的證明.本題要求學生能夠結合已知結論解決問題,熟練掌握構造法證明不等式.
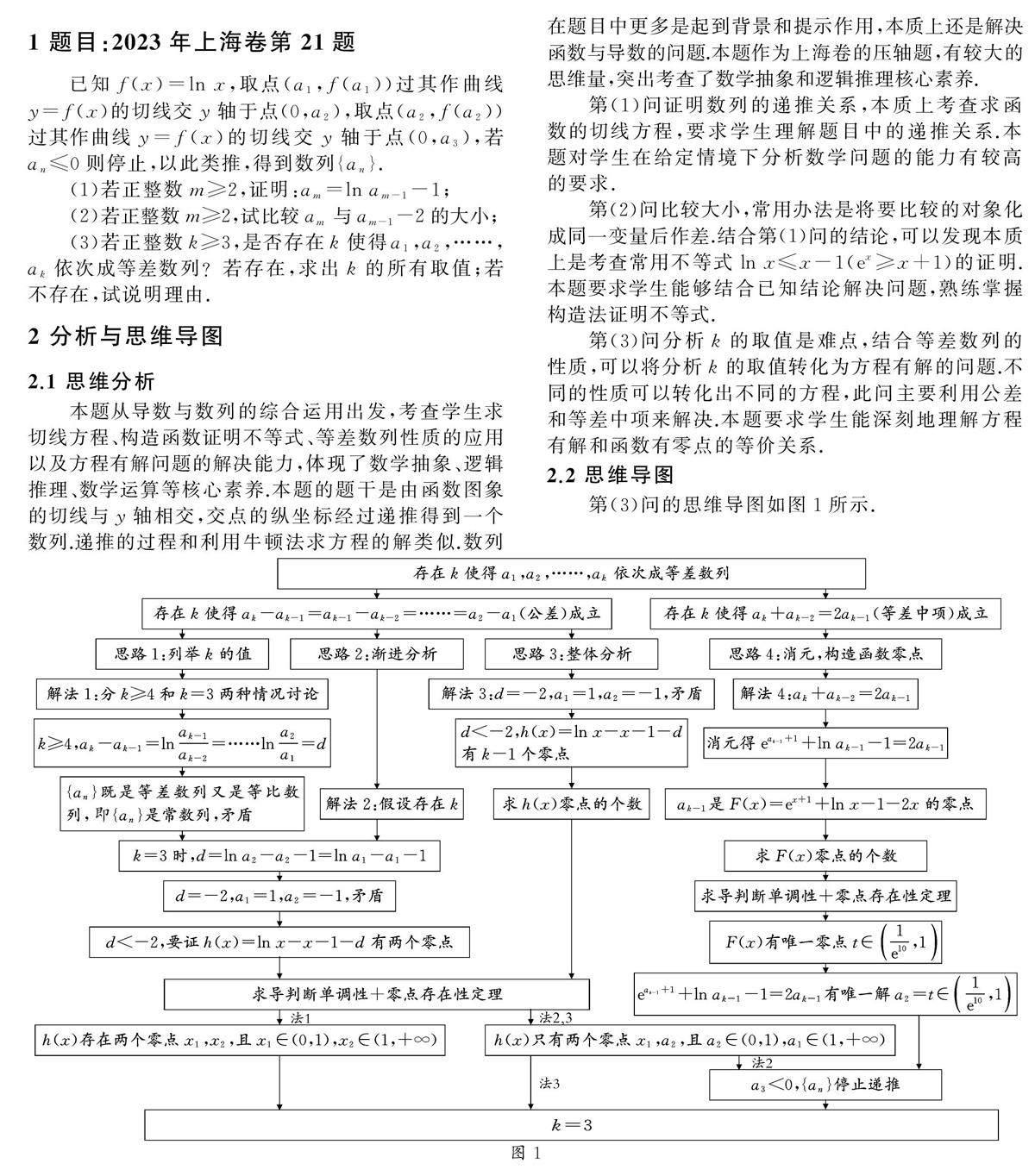
第(3)問分析k的取值是難點,結合等差數列的性質,可以將分析k的取值轉化為方程有解的問題.不同的性質可以轉化出不同的方程,此問主要利用公差和等差中項來解決.本題要求學生能深刻地理解方程有解和函數有零點的等價關系.

