發揮信息技術優勢 提升課堂教學效果

吳久輝

摘要：新課程改革的進一步深入，對高中數學的教學手段、教學方式等提出了全新的要求.將信息技術與高中數學教學相結合既能滿足學生的發展需求，也符合新課改的要求，在發展學生思維、培養學生的創新意識、提升教學質量等方面發揮著重要的作用.本文中展示了幾何畫板在高中數學教學中的優勢，以期通過適時、適度、適當的應用，提升課堂教學效果，實現學生的可持續發展.

關鍵詞：信息技術；幾何畫板；教學效果

數學是一門比較抽象的學科，有些內容僅憑教師單方面的講授學生很難理解和掌握.基于此，在高中數學教學中，教師有必要更新教學方式和教學手段，將抽象的內容生動、直觀地呈現出來，這樣既易于學生理解和掌握，又可以調動學生參與的積極性，有利于深度學習的達成.而將信息技術與數學教學相結合，可以將知識系統、直觀地呈現出來，有效淡化數學知識的抽象感，使數學課堂豐富起來、生動起來，切實提升課堂教學效果［1］.在“直線和圓的位置關系”教學中，筆者借助幾何畫板，將圓與直線的位置關系形象、直觀、準確地呈現出來，在幫助學生理解知識的同時，激發學生學習興趣，提升學生數學思維能力和數學核心素養.現結合具體案例，談談幾何畫板的教學優勢.

1 巧借幾何直觀，促進理解

解析幾何既是教學重點，也是教學難點，許多學生在學習這部分內容時容易產生畏難情緒，從而影響最終學習效果.確實，對于初學解析幾何的高一新生來講，這部分內容比較抽象，涉及層面較廣，綜合應用比較靈活，僅憑教師講授很難讓學生將相關知識、方法等學懂、吃透.在實際教學中，為了讓學生更加直觀地感悟直線與圓的位置關系，大多教師會滲透數形結合思想，以期借助形的直觀淡化問題的抽象性，幫助學生克服畏難情緒，提高學生參與課堂的積極性.在具體實施過程中，教師若選擇課上手工繪圖，這樣不僅會浪費寶貴的課堂時間，而且難以準確表達蘊含其中的數學關系.而利用幾何畫板可以有效解決以上問題，快速、直觀、準確地呈現圖形，更易于學生理解和掌握.

案例1?中點軌跡問題

教學中，教師設計了如下幾個問題：

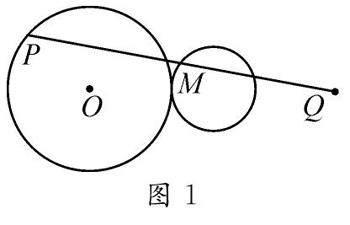
（1）已知P是定圓O上一動點，Q為圓O外一定點，連接PQ，M是PQ的中點，當P在圓O上運動時，點M的軌跡是什么？

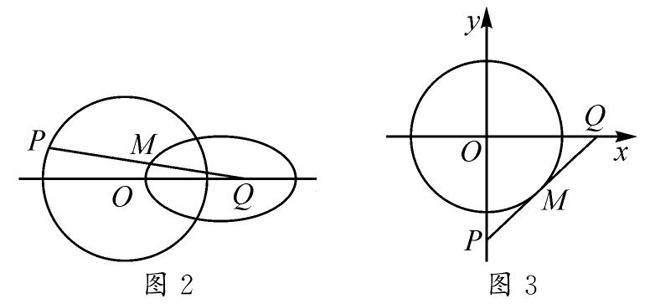
（2）已知P是定圓O上一動點，點Q在過圓心O的定直線上，且線段PQ為定長，M是PQ的中點，當點P在圓O上運動時，點M的軌跡又是什么？

（3）在平面直角坐標系xOy中，P，Q分別為y軸和x軸上的兩動點，且線段PQ為定長，M是PQ的中點，當動點P在y軸上運動時，M的軌跡又是什么？

教學中，教師先讓學生思考并提出自己的猜想，然后運用幾何畫板進行動態演示，讓學生借助圖形進一步觀察（如圖1～圖3），幫助學生加深對中點軌跡問題的理解.

通過直觀演示可以輕松得到如下結論：問題（1）中，中點M的運動軌跡是圓；問題（2）中，中點M的運動軌跡是橢圓；問題（3）中，中點M的運動軌跡是圓.

這樣借助幾何畫板就將中點軌跡的三個問題直觀、快速、準確地呈現出來了.通過經歷以上過程，學生可以感受軌跡的產生過程，有利于培養空間意識，提升直觀想象素養.另外，通過動態展示，抽象的問題會變得更加直觀、簡潔、生動，便于理解和掌握.通過經歷以上過程，還可以幫助學生積累豐富的活動經驗，有利于發展學生的數學思維和核心素養.

2 借助直觀精準，促進發現

直線與圓相結合的圖形運動問題是高考的一個重要考點，該類型的題目比較抽象，具有一定難度.在日常教學中，若教師僅是就題論題式的講授，將影響學生知識體系的建構，不利于學生解決問題能力的提升.因此在實際教學中，教師不妨借助多媒體的直觀化、系統化、精準化，引導學生對相關知識進行歸納總結，讓學生的腦海中形成清晰的知識脈絡，從而提高遷移水平[2].

對于兩個非同心圓的一般方程，若將兩圓的一般方程作差，則得到一個二元一次方程，即一條直線l的方程.該直線與已知兩圓可能會有一定的特殊的關系，這是一個值得探究的問題.兩圓的位置關系有多種，受其影響，直線l與兩圓的特定關系也會有所不同.這種不同很難單純地靠說或板書來表達，教學中可著重演示這一動態變化過程，引導學生在變化中逐漸抽象概括，從而發現規律.在具體實施過程中，教師不妨借助幾何畫板來動態演示，引導學生通過觀察、抽象概括等過程，提高教學實效性.

案例2?直線和兩圓的位置與方程的關系

教學中，教師以兩圓相交這一位置關系為引例，開啟探究之旅：

問題?如圖4，作兩相交圓圓O1和圓O2，其交點為M，N，令點M，N所在直線為l，在直線l上取一點P（異于點M，N），過點P分別作圓O1和圓O2的切線PE，PF，連接O1O2.結合圖形，說說你有何發現？

學生通過直觀觀察易于發現：（1）在直線l上任取一點作兩圓的切線，則切線長相等；（2）直線l與兩圓的連心線垂直.基于以上發現，教師讓學生度量兩圓及直線的方程，觀察、猜想并驗證它們之間的關系.猜想及證明過程如下：

猜想：若圓O1和圓O2相交，則直線l的幾何意義是兩圓的公共弦所在的直線.

證明：設P1（x1，y1），P2（x2，y2）是兩圓的交點，則有x21+y21+D1x1+E1y1+F1=0和x21+y21+D2x1+E2y1+F2=0成立，即P1（x1，y1）滿足方程（x21+y21+D2x1+E2y1+F2）－（x21+y21+D1x1+E1y1+F1）=0，整理得（D1－D2）x+（E1－E2）y+F1－F2=0.同理，P2（x2，y2）也滿足上式.所以直線l表示兩圓的公共弦所在的直線.

在此基礎上，教師讓學生繼續思考：兩圓相離、相切或內含時，是否有符合以上條件的直線l？這樣借助幾何畫板的直觀、快速、準確，打開了學生的思維大門，讓學生對蘊含于圖形中的一些特殊結論了然于心，有利于提升學生學習信心，發展學生數學核心素養.

3 提供實踐機會，提升素養

幾何畫板是研究幾何問題的重要工具，可以將抽象的知識和復雜的問題直觀地展示出來，從而為知識的理解和問題的解決提供便利.在現實教學中，幾何畫板以教師操作為主，這樣雖然高效，但是學生的思路被教師牽著走，學生的發現局限于教師的預設中，影響學生創新意識的培養.在實際教學中，教師可以提供機會讓學生自己操作，這樣既可以調動學生參與的積極性，又能激活學生的思維，提高學生的動手探究能力和創造力.在課堂教學中，只有真正將主動權交給學生，才能充分釋放學生的無限潛能，提升學習品質和教學有效性[3].

案例3?和兩個定圓相切的動圓圓心軌跡

如圖5，已知兩定圓O1和O2的半徑分別為r1，r2，動圓M與兩圓相外切.

（1）如果兩定圓相離，那么圓心M的軌跡是什么？

（2）如果兩定圓外切，情況會怎樣？

（3）如果兩定圓相交、內含、內切，又能得到怎樣的結論？

（4）如果兩定圓內切于動圓M，圓心M的軌跡又會怎樣呢？

對于以上問題，若直接讓學生推理分析，容易滋生學生的畏難情緒，因此教師不妨提供機會讓學生動手實踐探究，讓學生通過操作、觀察、分析、歸納等活動輕松地解決問題.另外，通過動手實踐探究形成的直觀認識，會給后續的推理驗證提供助力，有利于學生發現、分析和解決問題能力的提升.

事實證明，適度地將幾何畫板等多媒體技術應用于數學教學實踐中，可以使抽象、枯燥的數學知識變得形象、直觀、生動，可以有效激發學生學習興趣，從而讓學生的學變得更加積極、主動.值得注意的是，在實際操作中，教師切勿獨攬課堂，要提供機會讓學生去操作、去發現，這對學生提高自主探究能力、發展直觀想象素養、提升數學思維能力等都是極其有益的.同時，教學中要提供機會讓學生去合作、交流，讓學生充分體會繪圖的樂趣以及體驗發現的喜悅，充分激發學生的主體性和主動性，促進學生數學核心素養的落實.

總之，幾何畫板作為優質的教學軟件，操作簡單，功能強大，將其應用于教學能發揮傳統教學無法比擬的作用.在實際教學中，教師要適時、適度、適當地加以應用，充分發揮其直觀、生動、快捷等優勢，加快新知內化進程，助力學生全面提升.

參考文獻：

［1］閔啟蒙.幾何畫板在高中數學教學中的應用策略[J].當代家庭教育，2020（7）：97.

［2］劉衛富.高中數學運用《幾何畫板》輔助解題的探究[J].數理化解題研究，2020（3）：28-29.

［3］黃山.信息技術環境下的三角函數教學——淺談幾何畫板在教學中的運用[J].考試周刊，2019（47）：86-87.