跨越抽象與現實邊界:高中數學跨學科教學模式探索與實踐
金玉明

摘要:跨學科教學有助于拓展數學思維,深化學習意識,形成知識體系,讓學生以數學的方式理解生活、理解世界.本文中以新課程教育理念為基礎,從學生創新思維、探究精神、數學能力發展等角度入手,概述了跨學科視角下高中數學教學實踐路徑,通過多學科知識交叉滲透與活動方案設計,培養學生數學創造思維和解決問題能力,提高數學素養與學習能力.
關鍵詞:高中數學;跨學科教學;核心素養;學習能力
新課標強調以培養學生的數學情感、理智、創造力和精神潛能為目的,教師應推動多學科知識之間的銜接融合,喚醒學生的數學思維,引導學生在思辨性實踐學習中透過思考、演算的學習過程進行深度學習,找到解決問題的飛躍性方法.數學知識具有獨特的公式結構和嚴密的符號體系,與各個學科之間相互關聯、相互作用,彼此影響.教師在跨學科教學視角下,要綜合考慮時間、空間、自然、人文、社會、科學等要素,實現學生數學素養與創新精神的協調發展.
跨學科又稱為交叉學科,每一門學科都不是孤立的,學科間或多或少都存在交叉重疊.在實際操作中,跨學科教學的主體并不局限于“教師+教師”,也可以是“教師+學生”“學生+學生”“教師+專家”等.以數學為主體的跨學科教學存在如下問題:高中各門學科之間知識點交集眾多,但目前教學各自為政,缺乏滲透融合.采取以數學為主體的跨學科教學的方法,對高中課程進行整合,汲取各學科教師的智慧,可以克服各學科分割過細、知識零散的弊端,使學生在學習時形成更為有序和寬廣的知識網絡,同時還可實現從學科教學到學科育人的跨越.
1 關聯現實問題,提高應用思維
數學不僅是科學、工程、生活必不可少的基礎工具,更是學好物理、化學等學科的基石.教師在跨學科教學中,要著眼于學生數學問題求解能力、決策能力與批判性思維的發展,激發學生的內在學習興趣,培養學生從數學角度自主發現、分析、提出問題的能力,讓學生在關聯已有經驗的基礎上,加強數學知識的應用,提高數學思維能力.
例如,教學“向量的應用”時,教師可提出問題:“同學們有沒有兩個人一起提包的經歷?怎樣提包更省力?”讓學生用向量知識來解釋力的合成問題,激發學生對數學問題的思考和物理現象的探索熱情.
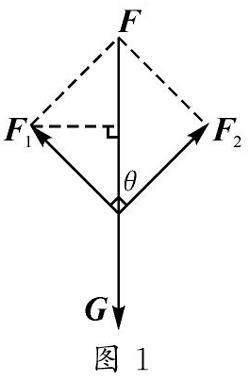
當學生結合物理觀點對問題進行解釋時,會對向量的概念、性質、基本運算印象更深刻.在物理現象的解釋中,通過與現實生活之間的聯系探索問題,分析F,G[WTBX],θ三個量,用數學知識對問題做出合理解釋:
如圖1,設|F[WTBX]1|=|F[WTBX]2|,由向量的平行四邊形法則、直角三角形等知識,可知F1,F2[WTBX]之間的夾角越小越省力,越大越費力.
數學既是定義物理量的依據,也是解決物理問題的工具.一次函數、二次函數、三角函數、平面幾何,都可與物理、化學研究,觀察,試驗,驗證等相關聯,擴展學生的數學領域與認知.
教師在跨學科教學中要將“無意識”的理性思考過程轉化為“有意識”的思考過程,激發學生內在的數學潛能,讓學生將數學知識、數學能力應用于分析、解決實際問題中,促進所學知識的遷移.
2 融入歷史素材,感悟思想智慧
新課標中提出,數學課程應解讀數學所蘊含的思想文化,有針對性地整合數學的思維、語言、精神,重構課堂內容.因此,教師在講授過程中,要聯系社會、生活、文化,揭示數學語言所蘊含的寓意、哲理,讓學生在數學概念、定理的持續內化和思考過程及數學內在邏輯與文化思想的探索體驗中,加深知識概念的理解,發展數學思維能力.
例如,教學“等差數列”時,教師可引入數學家高斯的故事,10歲的高斯解決了求等差數列1,2,3,……,100前100項和的問題,高斯的算法高明在哪里?如果我們一般化,在等差數列{an}中,把首項1換成a1,100換成末項an,把a1+a2+a3+……+an 稱 為 數 列{an}的前n項和,用Sn來 表 示 , 即Sn=a1+a2+a3+……+an,那么剛才的對應關系就應該變為(1+100)對應(a1+an),那么數列前n項和就是Sn=a1+a2+a3+……+an=[SX(]n(a1+an)[]2[SX)].
在教學“空間幾何體的表面積和體積”時,會用到圓的面積公式為S=πr2,該公式可以使用定積分來證明,公元263年我國劉徽提出的割圓術,也是同一思想.這樣的例子不勝枚舉,教師在課程設置上,要將數學與人文教育置于同等地位,鼓勵學生以合作探究的方式學習,讓學生在感受數學家的智慧與魅力的同時,自主觀察、操作、探究、歸納,感受數學歷史進程中所展現出的思維與方法,了解數學知識中所獨有的性質和特征.
3 整合人文精神,嚴謹辯證求實
數學概念、定理、法則等符號語言,是對科學真理的嚴謹表述,數學追求問題更加科學、合理的解答,數學的思想精神具有豐富的哲學內涵.教師在跨學科教學中要將人文教育滲透到數學課堂,深層挖掘數學知識的人文價值,將二者有機地結合在一起,真正做到全方位育人.
教師在解題教學過程中應注重人文思想的滲透,讓學生在解題學習中能深入理解數學概念、性質的生成過程.教師可結合畢達哥拉斯和畢達哥拉斯學派、割圓術、圓周率、積分的概念、切線的斜率等數學思想史,向學生講解數學家努力鉆研、勇于探索創新的人文精神,理解數學文化所蘊含的人文精神.
教師在課程體系的構建上,要重視文理兼容的通才教育,打通文、理之間的隔閡壁壘,拓寬學生的知識面,促進學生知識、能力、文化、素質全面發展.
數學語言符號和思想體系對于學生整個生命成長而言至關重要,能起到德育、智育、體育、美育、勞育等多方面的實效,教師要通過我國數學家的事例,激發學生的愛國主義熱情,增強民族自豪感和文化自信,激勵學生刻苦學習、積極進取.
4 擴展理性思維,培養數學精神
高中數學跨學科教學要強調知識跨界與思維能力的自主建構,跨學科學習并非簡單的知識疊加,教師要整合科學、社會、數學的功能與方法,營造一個人人參與的學習氛圍,讓學生像數學家一樣自主收集材料、信息,評估、制訂解決問題的方案.
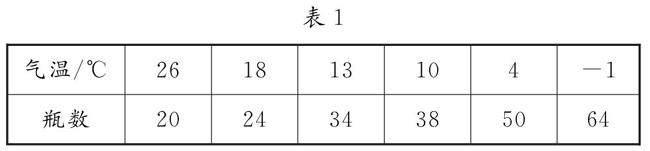
例如,教學“線性回歸方程”時,提出問題:超市為了解礦泉水銷售量與氣溫之間的關系,隨機統計并繪制了6天內賣出的礦泉水瓶數與氣溫的對照表(表1),假設某一天的氣溫是-5℃,你能根據這些數據預測超市賣出的礦泉水瓶數嗎?
教師以任務驅動的形式,引導學生作出散點圖.以橫坐標x表示氣溫,縱坐標y表示礦泉水銷量,建立如圖2所示的平面直角坐標系.教師提問:怎樣表示礦泉水銷量與氣溫之間的關系?
怎樣的直線最好?用直線方程y[KG-0.6mm]︿=bx+a擬合散點圖中的點,使得該直線與散點圖中點最接近.怎樣衡量直線y[KG-0.6mm]︿=bx+a與六個點的接近程度?教師引導學生找出并應用
教師搭建知識結構、明確任務要求后,要將學習的權利交給學生,讓學生自主探索,在相互協作中交流,經歷整個學習過程,拓展了學生的思維寬度,提高學生數學思維與知識遷移能力.在此研究下,歸結出一個高中數學跨學科教學模式,如圖3所示.
概言之,高中數學跨學科教學有助于提高學生數學興趣、創新思維與學習能力,教師在數學課堂中要從學生全面發展角度入手,為他們建立一個完整、有趣的探索任務框架,讓學生在解決問題的過程中,能從多學科視角展開獨立構想、交流,找到問題的本質,提出解決問題的新思想、新方法.教師在課堂教學中要關注學生的情感體驗,以學生的思維水平和認知能力為切入點,創設自主實踐體驗活動,讓學生在多樣、生活化、真實的探索空間與交流、質疑過程中,廣泛聯系多學科知識分析、解決問題,實現抽象思維與數學能力的綜合發展.

