以“圓錐曲線”教學(xué)為例談數(shù)形結(jié)合思想的滲透

聞君

摘要：數(shù)形結(jié)合既是一種數(shù)學(xué)思想方法，也是一種解題策略，是溝通數(shù)與形的橋梁，連接具體與抽象的紐帶.本文中以“圓錐曲線”相關(guān)內(nèi)容的教學(xué)為例，充分展示了數(shù)形結(jié)合在加強(qiáng)基礎(chǔ)知識(shí)理解、提高學(xué)生解題能力、發(fā)展學(xué)生數(shù)學(xué)思維能力和數(shù)學(xué)能力等方面的優(yōu)勢(shì)，以期在日常教學(xué)中，通過合理有效的滲透，實(shí)現(xiàn)個(gè)體認(rèn)知結(jié)構(gòu)的優(yōu)化和解題能力的提升，促進(jìn)學(xué)生的全面發(fā)展.

關(guān)鍵詞：數(shù)形結(jié)合；思維能力；數(shù)學(xué)能力

數(shù)形結(jié)合將抽象思維轉(zhuǎn)化為形象思維，從而實(shí)現(xiàn)抽象、復(fù)雜問題直觀化、形象化，凸顯數(shù)學(xué)本質(zhì)，促進(jìn)學(xué)生分析和解決問題能力的提升[1].數(shù)形結(jié)合實(shí)現(xiàn)了“數(shù)”與“形”相互溝通，其為數(shù)學(xué)學(xué)習(xí)提供方向，有利于數(shù)學(xué)能力和數(shù)學(xué)素養(yǎng)的發(fā)展與提升.

“圓錐曲線”既是高中數(shù)學(xué)的重點(diǎn)，也是教學(xué)難點(diǎn)，還是高考的考點(diǎn)，其在高中數(shù)學(xué)教學(xué)中的地位和價(jià)值是不言而喻的.在“圓錐曲線”教學(xué)中，教師中應(yīng)該重視滲透“數(shù)形結(jié)合”思想，以此借助圖形的形象、直觀激發(fā)學(xué)生的學(xué)習(xí)興趣，加深相關(guān)知識(shí)的理解，幫助學(xué)生突破教學(xué)的重難點(diǎn)，提高學(xué)生應(yīng)用相關(guān)知識(shí)解決問題的能力.那么在圓錐曲線教學(xué)中，如何發(fā)揮數(shù)形結(jié)合思想方法的優(yōu)勢(shì)，以助學(xué)生更好地把握知識(shí)，提高教學(xué)有效性呢？以下筆者結(jié)合自己的教學(xué)經(jīng)驗(yàn)談幾點(diǎn)粗淺的認(rèn)識(shí)，供參考！

1 巧借數(shù)形結(jié)合，促進(jìn)知識(shí)理解

高中范圍內(nèi)圓錐曲線主要包括橢圓、雙曲線和拋物線這三大板塊，這三大板塊的內(nèi)容具有一定的抽象性和相似性.在日常教學(xué)中，若教師直接呈現(xiàn)相關(guān)概念、結(jié)論等讓學(xué)生熟記，很容易造成混淆，從而影響解題效果和學(xué)習(xí)信心.基于此，在研究定義、性質(zhì)等相關(guān)內(nèi)容時(shí)，教師不妨滲透數(shù)形結(jié)合思想，以此充分發(fā)揮圖形直觀的優(yōu)勢(shì)，幫助學(xué)生在腦海中形成清晰的知識(shí)脈絡(luò)，建構(gòu)完善的知識(shí)體系[2].

例如，在學(xué)習(xí)“橢圓”的定義時(shí)，為了讓學(xué)生更好地理解橢圓的定義，教師可以先引導(dǎo)學(xué)生將文字語言轉(zhuǎn)化為符號(hào)語言——|MF1|+|MF2|=2a（其中|F1F2|<2a），在此基礎(chǔ)上，借助圖形來觀察△MF1F2，并引導(dǎo)學(xué)生利用“三角形的三邊關(guān)系”去理解定義，以此加深對(duì)“|F1F2|<2a”的理解.學(xué)習(xí)了雙曲線的定義后，教師可以用同樣的方式讓學(xué)生理解，為什么定義中強(qiáng)調(diào)“|F1F2|>2a”.這樣通過文字語言、符號(hào)語言和圖形語言的相互轉(zhuǎn)化，學(xué)生腦海中有了圖形和定義，日后在研究圓錐曲線的標(biāo)準(zhǔn)方程時(shí)，自然可以借助圖形獲得等量關(guān)系，從而輕松地實(shí)現(xiàn)由“形”到“數(shù)”的轉(zhuǎn)化，增強(qiáng)學(xué)習(xí)信心.

又如，在教學(xué)“拋物線的定義”時(shí)，教師可以利用幾何畫板進(jìn)行演示，讓學(xué)生體會(huì)“數(shù)隨形動(dòng)”，借助幾何直觀獲得其中的數(shù)量關(guān)系，得到拋物線的定義.這樣借助形使拋物線的定義更加生動(dòng)形象，更易于學(xué)生理解和掌握，以便學(xué)生建立關(guān)于拋物線的圖形和數(shù)量關(guān)系的知識(shí)體系，為數(shù)學(xué)知識(shí)的應(yīng)用打下堅(jiān)實(shí)的基礎(chǔ).

2 巧借數(shù)形結(jié)合，直觀把握性質(zhì)

在日常教學(xué)中發(fā)現(xiàn)，學(xué)生能夠快速地求出圓錐曲線的標(biāo)準(zhǔn)方程，但是在描述各量之間的關(guān)系，并用蘊(yùn)含其中的數(shù)量關(guān)系解決問題時(shí)，部分學(xué)生常感無從下手.究其原因就是學(xué)生的腦海中并未建立直觀圖形，這樣學(xué)生在表述其中蘊(yùn)含的數(shù)量關(guān)系時(shí)就顯得缺乏邏輯性和層次感.基于此，教學(xué)中，教師若能借助圖形將其中蘊(yùn)含的數(shù)量關(guān)系直觀地表示出來，定能達(dá)到事半功倍的效果.

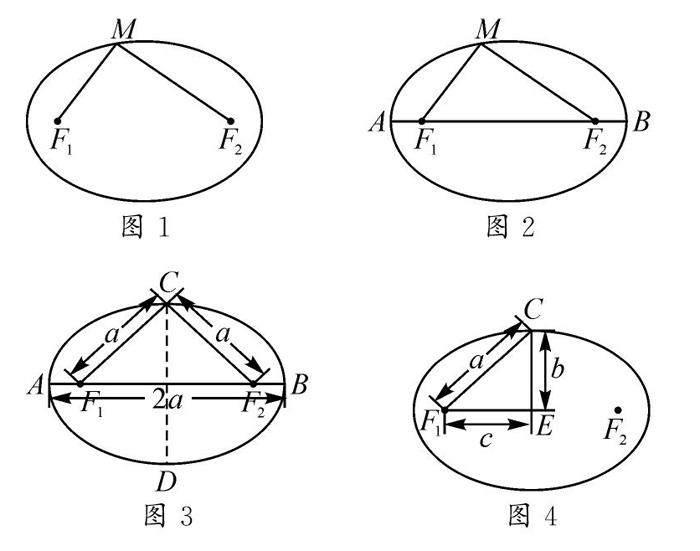
例如，橢圓標(biāo)準(zhǔn)方程中引入a，b，c三個(gè)量，教學(xué)中教師不僅要讓學(xué)生知道相關(guān)的量分別代表的幾何意義，還要提供機(jī)會(huì)讓學(xué)生去提煉其中的等量關(guān)系.在實(shí)際教學(xué)中，為了讓學(xué)生更好地把握知識(shí)，教師給出圖1～4所示的圖形讓學(xué)生觀察、抽象.如對(duì)于圖1，M是橢圓上一點(diǎn)，F(xiàn)1，F(xiàn)2為橢圓的焦點(diǎn)，則有|MF1|+|MF2|=2a；對(duì)于圖2，若橢圓的長(zhǎng)軸端點(diǎn)分別為A，B，F(xiàn)1，而F2為橢圓左、右焦點(diǎn)，則|AF1|+|AF2|=|AF1|+|BF1|=2a；對(duì)于圖3，若橢圓短軸端點(diǎn)是C，D，則|CF1|+|CF2|=2a，|CF1|=|CF2|=a；對(duì)于圖4，結(jié)合勾股定理，易得a2=b2+c2.這樣借助圖形的直觀可以幫助學(xué)生更好地理解其中蘊(yùn)含的數(shù)量關(guān)系，從而為解題帶來便利.

又如，學(xué)習(xí)了“拋物線的性質(zhì)”后，教師給出了這樣一道題：拋物線y=4x2的焦點(diǎn)坐標(biāo)是[CD#3].該題是一個(gè)基礎(chǔ)題，但是解題效果并未達(dá)到預(yù)期，部分學(xué)生因誤認(rèn)為2p=4，所以得到了（1，0）這一錯(cuò)解.對(duì)于這一錯(cuò)誤，若教師給出拋物線標(biāo)準(zhǔn)方程讓學(xué)生觀察、套用，學(xué)生雖然能夠獲得正解，但是這樣的教學(xué)缺少了一定的探究性，難以誘發(fā)學(xué)生的深層思考.基于此，教師不妨引導(dǎo)學(xué)生將方程轉(zhuǎn)化為x2=14y，并畫圖.讓學(xué)生借助圖形去觀察、去體會(huì)，從而使問題迎刃而解.在日常教學(xué)中，當(dāng)學(xué)生解題過程中出現(xiàn)一些模棱兩可的情況時(shí)，教師可以引導(dǎo)學(xué)生去畫圖，直觀觀察、理解，以此消除困惑，提高學(xué)習(xí)信心.

再如，有這樣一道問題：方程（x+3）2+y2+（x－3）2+y2=10表示什么？問題給出后，先讓學(xué)生獨(dú)立求解.從解題反饋來看，學(xué)生看到該方程就聯(lián)想到兩點(diǎn)間的距離公式，從而得到的結(jié)論是：平面內(nèi)一點(diǎn)（x，y）到（－3，0）和（3，0）兩點(diǎn)的距離之和為10.顯然從代數(shù)角度分析還不夠具體、形象，需要從幾何角度進(jìn)一步抽象：平面內(nèi)一點(diǎn)到兩定點(diǎn)的距離之和為常數(shù)，且該常數(shù)大于兩定點(diǎn)間的距離，根據(jù)橢圓的定義可知，該點(diǎn)的軌跡是橢圓.學(xué)生通過分析知曉該點(diǎn)的軌跡是橢圓后，教師可以預(yù)留時(shí)間讓學(xué)生畫出橢圓，并寫出a，b，c的值.這樣，通過數(shù)與形的相互轉(zhuǎn)化，順利地得出該方程表示焦點(diǎn)在x軸上的橢圓，其標(biāo)準(zhǔn)方程為x225+y216=1.

學(xué)習(xí)了圓錐曲線的相關(guān)性質(zhì)后，教師不要急于讓學(xué)生去記憶，應(yīng)該嘗試引導(dǎo)學(xué)生借助圖形去分析、去抽象、去感悟，這樣可以使圓錐曲線的性質(zhì)更加直觀、形象，以此幫助學(xué)生直觀化地把握性質(zhì)，有效提高解題效率和解題準(zhǔn)確率.

3 巧借數(shù)形結(jié)合，將幾何問題代數(shù)化

在學(xué)習(xí)數(shù)學(xué)的過程中，既要借助形的直觀來理解數(shù)，也要用數(shù)的嚴(yán)謹(jǐn)分析形，通過形與數(shù)的相互轉(zhuǎn)化，形成正確的解題思路，提升學(xué)生分析和解決問題的能力.

例如，直線與圓錐曲線的位置關(guān)系是高考的一個(gè)重要考點(diǎn).在研究位置關(guān)系時(shí)，若僅從形的角度去觀察，顯然不具說服力，為此在研究位置關(guān)系時(shí)，需要將幾何問題代數(shù)化，運(yùn)用代數(shù)知識(shí)來解決.在研究位置關(guān)系時(shí)，教師可以鼓勵(lì)學(xué)生聯(lián)想研究圓與直線位置關(guān)系的方法，利用方程思想解決問題，通過判斷一元二次方程的實(shí)根個(gè)數(shù)，確定圓錐曲線與直線的位置關(guān)系.

在學(xué)習(xí)的過程中，教師要有意識(shí)地引導(dǎo)學(xué)生進(jìn)行新舊知識(shí)的類比，通過新與舊的有效溝通，提高學(xué)生自主探究能力，幫助學(xué)生建構(gòu)完善的體系.

4 巧借數(shù)形結(jié)合，拓展數(shù)學(xué)思維

數(shù)與形是相互聯(lián)系的有機(jī)整體，二者相互補(bǔ)充，密不可分.在研究圓錐曲線中的數(shù)量關(guān)系和幾何關(guān)系時(shí)，教師要有意識(shí)地引導(dǎo)學(xué)生將二者有效地聯(lián)系在一起，通過彼此的相互轉(zhuǎn)化實(shí)現(xiàn)化抽象為具體、化無形為有形，幫助學(xué)生快速地形成解題策略，提高解題效率[3].

例如，學(xué)習(xí)了雙曲線相關(guān)知識(shí)后，教師給出了這樣一道練習(xí)：已知雙曲線x29k2－y24k2=1與圓x2+y2=1沒有交點(diǎn)，求實(shí)數(shù)k的取值范圍.從解題反饋來看，學(xué)生看到“交點(diǎn)”二字，首先想到的就是利用方程思想解決問題，將兩方程聯(lián)立，通過消元將其轉(zhuǎn)化為一元二次方程，根據(jù)Δ<0，得到不等式，從而通過解不等式，求得k的取值范圍.該思路是合理的，但是解題過程中涉及復(fù)雜的運(yùn)算，這樣不僅會(huì)占用較多的解題時(shí)間，而且容易出現(xiàn)錯(cuò)解的風(fēng)險(xiǎn).基于此，不妨換個(gè)角度，將代數(shù)問題幾何化，借助圖形的直觀尋找解題的突破口.結(jié)合已知易得到一個(gè)圓心在原點(diǎn)，半徑為1的圓，而該圓與焦點(diǎn)在x軸上的雙曲線無交點(diǎn)，則說明雙曲線的實(shí)半軸大于圓的半徑，所以由a=9k2=|3k|，可得|3k|>1.顯然借助形來分析，問題會(huì)變得更加簡(jiǎn)潔，有效地優(yōu)化了運(yùn)算過程，提高了解題效率和解題準(zhǔn)確率.

總之，無論是從加深知識(shí)理解的角度，還是從提升解題能力的角度來分析，研究圓錐曲線離不開“數(shù)”與“形”的相互轉(zhuǎn)化.因此，在日常教學(xué)中，教師要將“數(shù)形結(jié)合”思想方法融于圓錐曲線的課堂教學(xué)實(shí)踐中，讓學(xué)生充分感知數(shù)形結(jié)合的應(yīng)用價(jià)值，以此培養(yǎng)數(shù)形結(jié)合意識(shí)，提升學(xué)生數(shù)學(xué)核心素養(yǎng).

參考文獻(xiàn)：

［1］郭文.數(shù)形結(jié)合思想在高中數(shù)學(xué)解題中的運(yùn)用探究[J].科技資訊，2020（10）：237-238.

［2］劉宗明.數(shù)形結(jié)合思想在高中數(shù)學(xué)教學(xué)中的實(shí)踐探究[J].數(shù)學(xué)學(xué)習(xí)與研究，2019（15）：31.

［3］賴敏.數(shù)形結(jié)合簡(jiǎn)析，分步突破細(xì)化——以圓錐曲線問題的突破為例[J].數(shù)學(xué)教學(xué)通訊，2021（6）：79-80，88.