基于UbD理論的“數列”單元教學設計

李曉宇

摘要：文章基于UbD理論的基本思想，制定了理論下的逆向單元教學設計框架，即要素分析、確定預期結果、確定合適的評估證據、設計學習體驗四個階段.以人教A版選擇性必修第二冊“數列”單元為例，進行單元設計，致力于促進學生深層次理解知識，把握數列的本質，提升學生核心素養.

關鍵詞：UbD理論；數列；單元教學設計

UbD理論是追求理解的逆向教學設計，由格蘭特和杰伊提出，“逆向”體現在將教學評價置于教學活動之前.同時，理論提供了逆向設計的三個階段，即確定預期結果、確定合適的評估證據、設計學習體驗和教學.階段一，強調提煉單元的大概念以及基本問題；階段二，強調評估證據來源于真實性任務中學生的表現；階段三，強調教學要基于目標，要能夠激發學生的興趣，能夠促進學生的深層次理解及遷移運用.基于此，以人教A版選擇性必修第二冊“數列”單元為例進行逆向設計.

1 階段一：要素分析

要素分析是數列單元逆向設計的基礎，在其基礎上才能進一步提煉大概念、基本問題等.階段一基于課標、教材對數列單元進行學情、教材、重難點分析，如表1所示.

表1?數列單元要素分析

學情分析：

（1）小學、初中均涉及數列問題.例如，小學根據數字找規律題，通過對相鄰數字進行運算（如作差）尋找規律，涉及了簡單的等差數列；初中對一組數找規律并要求用含n的式子表示，涉及到數列的通項公式.

（2）必修第一冊在函數研究中，從函數的概念、表示方法，到函數性質的研究，再到基本初等函數的研究，都為數列單元的學習奠定了知識方法基礎.

（3）以往學生學習該單元存在的問題：課堂授課相關數學史知識涉及較少；學生學完后，對數列單元的知識沒有形成脈絡主線，處于碎片化狀態；教學過程以講授為主，學生積極性不高；學習以刷題、代入公式計算等為主，學生思維能力沒有獲得提升，知識沒有得到很好的理解以及遷移應用.

教材分析：

（1）章引言：更注重數列的函數本質，解釋了將其看作函數的原因；展示了學什么、怎樣學（抽象數學對象－研究性質—建立數學模型解決問題），以及培養學生哪些核心素養.

（2）節引言：新教材較舊教材，每一節前都有節引言，建立新舊知識間的聯系，介紹要學習內容的研究思路或者思想方法，體現認知過程的連貫性.

（3）新教材中思考與探究欄目數量增多，更重視通過問題啟發學生；同時問題的設置更注重對思想方法的引導而獲得，在欄目后也提供了問題的解答，更有利于學生自學.

（續表）

（4）章末小結的知識結構：核心知識的展現更完整，研究的邏輯線索更清晰，突出了數列與函數的聯系.

（5）部分知識順序發生了改變（如將遞增、遞減、常數列歸在數列的性質即單調性中研究，這樣的改變使得數列的學習與函數研究路徑一致），更有利于學生對數學知識本質的理解.

（6）選擇數學史素材，數列單元無論是概念的引入、求和方法的獲得，還是閱讀欄目以及習題等，都有中外數列故事的影子，文化內涵豐富；數列單元也充分利用信息技術工具等.

課標及重難點分析：

（1）重點：數列、等差數列、等比數列的概念及性質與應用.

（2）難點：從實例中抽象出數列的定義（由于排列好的一列數與數列定義有差距，學生需要具備較高抽象能力）；等差數列的定義（學生需要通過運算發現代數規律）；推導等差數列、等比數列的前n項和公式（需要通過邏輯推理、數學運算等途徑）；用等差、等比數列刻畫數學或現實中具有遞推規律的事物（學生需要具備一定的建模能力）.[HY]

2 階段二：確定預期結果

基于對要素的分析以及參考課程標準等，提煉出大概念即數列是一類特殊的函數，同時利用基本問題來架構目標，即思考成套相互關聯的問題，激發對問題的持續探究，同時與已有經驗建立有意義的聯系[1].如表2所示.

表2?確定預期結果

基本問題：

（1）為什么要學習數列？

（2）數列和函數有什么聯系？

（3）通項公式與求和公式有什么聯系？

（4）等差數列與等比數列有什么聯系？

（5）數列單元的基本思想方法是什么？

學生將會理解：

（1）數列學習的研究價值；（2）數列和函數的共性與差異；

（3）通項公式與求和公式的聯系；（4）思想方法學習的重要性.

學生將會知道：

（1）數列、等差數列、等比數列的概念，通項公式，前n項和公式，遞推公式；（2）數列的起源、發展及完善，了解蘊含的數學文化；（3）通過運算發現數列的規律，歸納共性；

（4）研究一個數學對象的基本路徑；（5）數學歸納法的原理以及應用.

（續表）

學生將能夠：

（1）類比函數的研究路徑研究數列；

（2）類比等差數列的研究思路研究等比數列；

（3）根據數列的等差、等比關系，通過運算、代數變換等一般性方法解決相應問題；

（4）感悟數學模型的現實意義與應用.[HY]

3 階段三：確定合適的評估證據

階段三需要思考“什么樣的表現能表明學生已經達到了要求？”“什么樣的證據表明學生思考了基本問題？”如表3所示.

表3?確定合適的評估證據

什么能夠證明學生理解所學知識？

表現性任務：

（1）分3個小組查閱資料，從數列的起源（遠古社會的計數、畢達哥拉斯形數、著名古代數列問題）、發展（歷史上等差、等比數列問題、數列與函數、古代數列求和方法）、拓展（斐波那契數列、漢諾塔游戲）三個視角整理數學史和數學文化元素，最終形成小論文，由學生講解并進行展示.

（2）繪制思維導圖，每節學習后，學生基于自身對數列知識的理解繪制思維導圖，并在其中標示學習中存在的難點，同時教師點評、學生互評，并對模糊知識進行討論講解；單元學習完成后，學生概括單元學習大概念，繪制單元思維導圖，提煉學習中涉及到的思想方法并進行舉例說明.

（3）單元復習階段，分小組設計數列單元專題教案（如數列與函數的聯系、求數列通項的方法和技巧、數列求和），學生主講，促進學生對知識、方法的深層次理解.

（4）現實情境中數列的簡單應用，培養學生數學建模、運算求解、創新等關鍵能力.

其他證據：

（1）教師課上觀察學生學習狀態、小組討論情況、上課回答問題情況；課下及時與學生進行對話，學生自評學習狀態、知識掌握情況以及情感態度問題.

（2）隨堂檢測與單元測試：對課堂基礎知識的掌握，對單元整體知識的掌握，對大概念、基本問題的掌握與回答情況.

（3）對理解的非正式檢查，如檢查學生的錯題集、日常作業、基于自身整理的難點合集等.

（4）學生自評或互評錯題集的利用率、思維導圖的完整性以及對進一步學習的有效性.[HY]

4 階段四：設計學習體驗

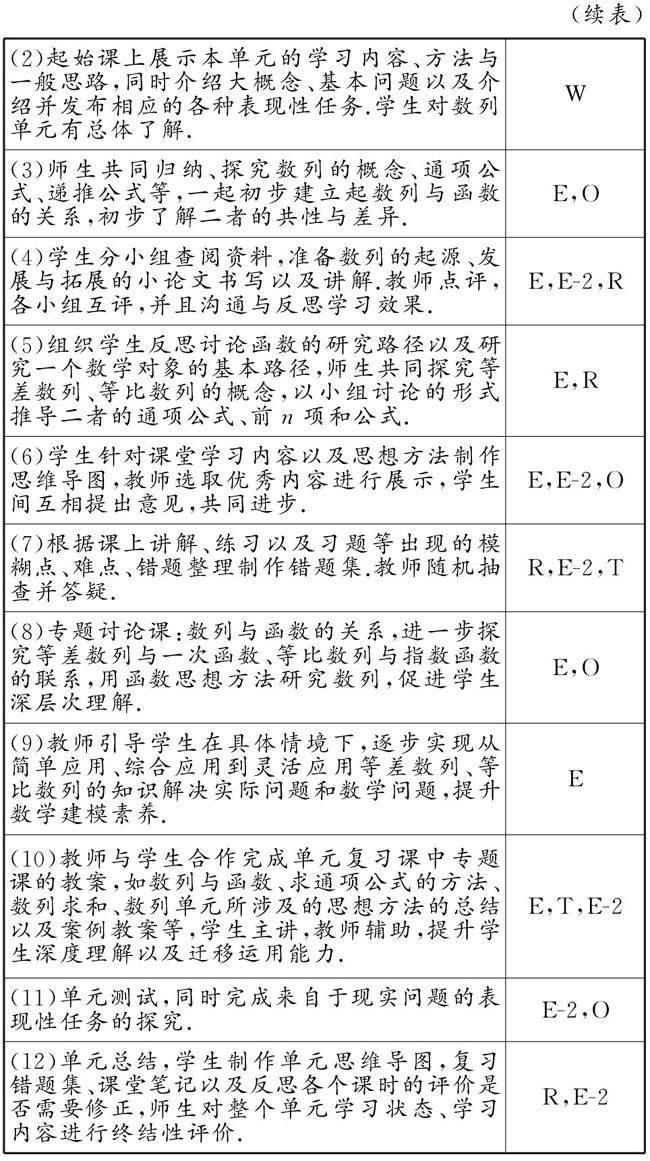
階段四（如表4所示）中，需要吸引性和有效性的學習活動和教學，喚起和產生預期的理解，激發學習興趣，使表現性行為成為可能.同時利用UbD理論中的WHERETO要素（其中W為學習方向、H為吸引、E為體驗和探索、R為反思、E-2為評價、T為量身定制、O為組織）[1]優化我們的設計，將其滲透在教學活動的各個環節.

UbD理論中的“逆向”“理解”“大概念”“基本問題”等思想為單元教學設計與實踐提供了指導與參考，同時理論也適用于單元下的課時教學，這樣的教學更具系統性、整體性；在確定合適的評估證據階段，注重評價主體與方式的多樣性，強調真實情境中學生的真實表現，多維度地搜集學生達到預期理解的證據，這些與課標的要求一致；在設計學習體驗環節，更關注學習者，關注他們的興趣，教學活動有利于培養學生的數學思維，激發學生的學習興趣，提高課堂效率，落實核心素養.

參考文獻：

［1］葛麗婷，施夢媛，于國文.基于UbD理論的單元教學設計——以平面解析幾何為例[J].數學教育學報，2020，29（5）：25-31.

［2］宋莉莉.用“數學的方式”學習數列——人教A版《數學》（選擇性必修第二冊）第四章“數列”的教材設計與教學思考[J].中學數學教學參考，2021（4）：4-9.