基于統計知識，高三復習建議

季佳雯

《普通高中數學課程標準（2017年版2020年修訂）》中多次出現“情境”一詞，《中國高考評價體系》也規定了高考的考查載體——情境，并以此承載考查內容，實現考查要求.數學情境是高考評價體系中最重要的創新之一，是實現“價值引領、素養導向、能力為重、知識為基”的考查目標的載體.數學試題情境一般取材于學生生活中的真實問題，貼近學生實際，具有現實意義，具備研究價值.

對統計知識（包括必修第二冊第九章“統計”、選擇性必修第三冊第八章“成對數據的統計分析”這兩個部分）的考查，正是依托情境而設置的基本考點之一，成為考查數學基礎知識，培養學生理性思維方式，提高學生分析、解決問題能力的一個重要載體.鑒于此，結合統計知識的基本特點，建議高三復習備考中應注意以下幾點.

1 夯實基礎，注重對數學概念的教學

高考對統計內容的考查，雖然試題千變萬化，但都以基本概念、基本思想為基礎，所以在復習中要以“課標”為軸，圍繞教材，對重點概念強化復習，夯實基礎知識.統計中的概念眾多，在復習備考中，教師要引導學生回歸教材，對教材中的基本概念進行梳理.統計的基本研究過程，即收集數據→整理數據→分析數據→統計推斷，

這條主線可以將統計的有關概念串聯起來.

例1?某家大型超市統計了八次節假日的客流量（單位：百人）分別為29，30，38，25，37，40，42，32，那么這組數據的第75百分位數為[CD#3].（39）

分析：根據統計應用情境，結合第75百分位數的定義加以合理計算，即可確定相應的答案.

點評：百分位數是在初中以及舊教材中對于樣本的特征數字所對應的中位數的基礎上進一步細化與深入，是用樣本估計總體中的一個新概念，為數據分析與決策問題提供更為詳細的數據信息，因而成為高考命題中的一個重要基本概念.

2 加強數據處理能力和運算能力的培養

“課標”對數學能力的要求中，在統計知識主要涉及數據處理能力，通過數據分析，借助統計知識與方法、公式等構建模型對數據進行分析、推斷，獲得結論；另外還涉及數學運算能力.這是該模塊知識中應用最為廣泛的兩種基本能力，要加以全面提升.

統計問題的核心是樣本數據的收集和處理方法，這也是高考考查的重點，所以在教學中要加強數據處理能力和運算能力的培養.

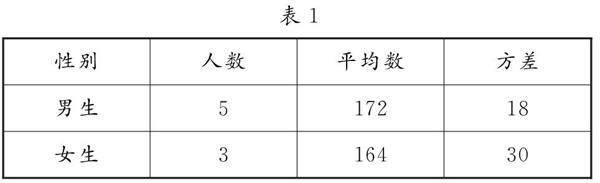
例2?某班級為了了解本班學生的身高情況，根據男、女學生所在的比例，采用樣本量按比例分配的分層隨機抽樣分別抽取了男生5名和女生3名，測量他們的身高所得的數據（單位：cm）如表1所示，根據表中數據，可計算出該校高中學生身高的總樣本平均數ω=[CD#3]；總樣本方差s2為[CD#3].（169；37.5）

分析：根據題意，利用總體的樣本平均數、方差的計算公式，通過合理分析與邏輯推理加以計算得到對應的答案.

點評：依托現實生活中的應用情境，以統計模塊的基礎知識為應用背景，借助平均數與方差公式，通過題中數據加以運算與比較.特別在對一些實際應用問題進行決策與判斷時，要有數據依據與基礎.

3 加強閱讀理解能力的培養

高考在統計方面的命題常以應用題為載體，重視統計的理論知識與實際生活相結合，題材內容豐富，注重考查考生各方面的能力與應用，往往考題的文字描述多，對考生的閱讀理解能力要求高.因此，要加強閱讀理解能力的培養，重視審題教學，教會學生準確理解題意，并通過數據分析來分析與處理問題.

例3?在南極，東南極冰蓋被稱為“沉睡的巨人”，是世界上最大的大陸冰川，包含了世界上大部分的冰.2022年在英國《自然》雜志發表的一篇論文指出，若《巴黎協定》的控溫目標未能達成，東南極冰蓋會因氣候變化影響而加速融化，到2500年，可能導致海平面上升2～5米.無獨有偶，2023年發表于《科學》雜志的新研究中，法國圖盧茲空間地球物理學和海洋學研究實驗室領銜的國際團隊揭了比之前預測的更大的冰川質量損失，全球溫度升高與冰川質量損失之間存在線性相關關系，有如表2所示的數據：

根據數據，繪制如圖1所示的散點圖，則下列說法正確的是（??）.（C）

①冰川消融百分比與溫度上升量存在正相關關系；

②由表中數據用最小二乘法得到的線性回歸直線一定經過點（1.25，41）

③記表中數據y1，y2，y3，y4，y5，y6的方差為s，若控溫措施有效，則冰川消融百分比將變為z%，且zi=0.6yi+0.005（i=1，2，3，4，5，6），那么z1，z2，z3，z4，z5，z6的方差將變為s′=0.6s+0.005.

A.①???[WB]

B.③???[WB]

C.①②???[WB]

D.②③

分析：通過素材的閱讀理解，根據題中的數據信息，結合散點圖可以判斷①，由線性回歸方程恒過樣本點的中心判斷②，由方差公式的性質判斷③，進而綜合來分析與判斷.

點評：以統計數據信息與圖形信息來創設問題場景，結合線性回歸方程的確定與性質、樣本估計值的計算，特別是方差公式的應用等，綜合考查數據處理、數學運算、直觀想象等素養，特別是閱讀理解能力.

4 注重數學核心素養的培養及思想方法的滲透

高考命題對統計模塊的要求同樣也是以知識為載體，能力立意為本，數學思想方法為靈魂，數學核心素養為統領來考查.在實際的統計模塊知識復習教學時，合理落實“四基”，全面培養“四能”.

例4?（多選題）有一組樣本數據x1，x2，x3，x4，x5，已知∑5i=1xi=10，∑5i=1x2i=30，則該組數據的（??）.（AC）

A.平均數為2

B.中位數為2

C.方差為2

D.標準差為2

分析：根據題中樣本數據的總和與平方和的數據信息，結合各對應樣本數據信息與對應的公式進行計算，即可正確判斷.

點評：數據信息與樣本估計值的公式等，是考查學生數學運算與數據處理能力與素養的一個重要場景.基于統計場景與應用，合理借助對應的數據信息與數據處理，達到合理考查的目的.

5 認真研究考題，把握高考命題方向

把脈高考命題方向是每位教師備考時的一項重要工作.近幾年高考對統計方面的考查內容和方向變化不大，保持較高的穩定性.高考主要考查統計中的基本概念，抽樣方法，樣本的數字特征，頻率分布直方圖以及其他統計圖表，總體百分位數，統計相關性，獨立性檢驗與回歸方程等知識的應用、決策問題.復習時要做好近年高考題的歸類整理，備考選題以全國卷為主，分類分組訓練，避免知識類型的“盲區”，并領會題目所蘊含的數學思想與方法.

例5?為研究農藥A對農作物成長的功效，在甲、乙兩塊試驗田播種同一種農作物，甲試驗田噴灑農藥A，乙試驗田沒有噴灑農藥A，經過一段時間后，從甲、乙兩塊試驗田各隨機選取100株幼苗，統計200株幼苗高度（單位：cm）如表3所示.

（1）分別求甲、乙兩塊試驗田中幼苗的平均高度的估計值（同一組中的數據以該組區間的中點值為代表）；（10.1cm）

（2）分別統計樣本中甲、乙兩塊試驗田幼苗高度小于10 cm和不小于10 cm的株數，完成下列聯表（表4），并依據小概率α=0.01的獨立性檢驗，分析是否噴灑農藥A與幼苗生長的高度有關聯？（有關聯）

分析：（1）根據題中數據信息，利用平均數公式加以分析與數學運算；（2）根據數據信息完成2×2列聯表，結合公式計算χ2的值，進而加以分析與推斷.

點評：以實際應用問題為情境，借助獨立性檢驗的創設與應用，合理融入統計知識中的頻率分布直方圖、樣本估計與平均值求解等，借助數形結合與數學運算等，綜合考查對應的統計知識與應用.

近年新高考中，涉及的統計模塊試題考查的內容緊密對標“課標”，與教材中知識內容所占的比例比較吻合，注重全面考查數學基本知識，并在此基礎上加以深化，在“通性通法”的基礎上，進行了適度的綜合與創新，提升創新性與應用性.