基于AGV的管道加熱器柔性作業車間調度方法研究
苗培仁,李曉東,胡 凱,劉 睿,劉 壯
(1.江陰市輝龍電熱電器有限公司,江蘇 江陰 214401;2.江蘇省柔性電加熱器工程技術研究中心,江蘇 江陰 214401; 3.江蘇省研究生工作站,江蘇 江陰 214401)
0 引言
柔性作業車間調度問題(FJSP,flexible Job shop scheduling problem)是柔性制造系統的核心,合理的調度方案可以有效降低車間成本,提高車間效率,使生產線穩定運轉,進而提高企業的效益[1]。自動導引車(AGV,automated guided vehicle)作為一種自動物流載具備智能、高效、安全性能好等優點,被廣泛應用于制造領域[2],其參與的集成調度逐漸成為生產調度優化領域的重點研究問題之一[3]。
在考慮運輸時間的柔性作業車間調度中,機器與AGV緊密相連,在調度過程中需同時對這兩個元素進行決策。群智能優化算法[4]具有較強的并行性和穩定性,它在解決優化問題時具有很好的搜索能力,因此被廣泛應用于車間調度問題求解。文獻[5]以綠色調度為重點,建立基于能耗閾值的機器、AGV聯合調度模型,使用改進帝國競爭算法求解模型獲得較優調度方案。文獻[6]提出一種融合調度模型,同時實現AGV路徑規劃與車間生產調度,使用混合遺傳鯨魚優化算法對其進行求解。文獻[7]以車輛裝配車間為研究對象,引入多AGV搬運工件,使用加入工序約束矩陣的改進遺傳算法對其進行求解。文獻[8]構建AGV和機器雙約束的多目標集成調度模型,綜合考慮多種時間因素,設計了貪心解碼策略和改進NSAG-II (Non-dominated Sorting Genetic Algorithm-II)算法求解模型。文獻[9]提出一種包含AGV調度和無沖突路徑規劃的遺傳算法用以解決 AGV約束下的FJSP。文獻[10]建立基于AGV的柔性作業車間自動化制造系統,提出多目標改進遺傳算法優化物流需求波動和生產周期。文獻[11]采用加入跳躍基因的遺傳算法求解AGV約束的FJSP,優化車間績效指標和AGV使用時長。
文獻[12]提出麻雀搜索算法SSA (Sparrow Search Algorithm)。該算法由于具有搜索精度高、收斂速度快等優點,一經提出便被廣泛應用于深度學習、路徑規劃等領域,但在柔性作業車間調度方面應用較少,且存在著很大的優化空間。在文獻[13-14]中,將麻雀搜索算法應用于FJSP,但都未深入討論AGV在FJSP中所起到的約束作用,因此提出一種改進麻雀搜索算法求解AGV、機器雙約束的柔性作業車間調度問題。
1 問題描述及模型建立
1.1 問題描述
管道加熱器生產車間具有多約束性、多目標性、加工柔性和運輸柔性等特點。其生產過程主要受到機器加工時間和物料運輸時間的約束,且在生產過程中要兼顧生產效率、生產成本、交貨期等指標。此外,管道加熱器的每道工序都可以在不同的機器上加工,并且具備不同的加工時間,即加工柔性。工件在機器之間的運輸依靠AGV實現,每個運輸任務可以選擇不同的AGV執行,因AGV所處位置的差異而具備不同的運輸時間,即運輸柔性。綜上所述,生產調度即在多個約束條件的限制下尋找可以兼顧多個生產指標的較優調度方案,因其復雜性被劃分為中的NP-hard (Non-deterministic Polynomial Hard)問題[15]。
為便于求解合適的調度方案,將柔性車間抽象為數學模型,即AGV和機器雙約束下的多目標FJSP,其可以描述為:設有n個工件在m個機器上加工,有v個AGV承擔運輸任務。每個工件有多道加工工序,加工順序固定,每道工序有多個可選的加工機器,且不同機器上的加工時間不同。對車間模型做出如下假設:
1)起始時刻所有工件與AGV均位于倉庫中;
2)AGV執行完當前任務后立即執行下一任務;
3)機器在同一時刻只能加工一個工件;
4)工序的加工過程無法中斷;
5)機器的緩沖區大小不限;
6)同一工件的相鄰工序在同一機器上加工時,不需要AGV運輸;
7)起始時刻所有AGV與機器均可用;
8)機器緩沖區中的工件加工順序由解碼方案確定;
1.2 模型建立
數學模型可直觀表達抽象的調度問題,其符號定義如表1所示。

表1 調度模型參數定義
∑Xi,j,k≤1
(1)
∑αv,Wi,j≤1
(2)
Te ,v,pre≤TZb,v,Wi,j
(3)
Pei,j-1≤TZe,v,Wi,j
(4)
TZe,v,Wi,j≤Tb,v,Wi,j
(5)
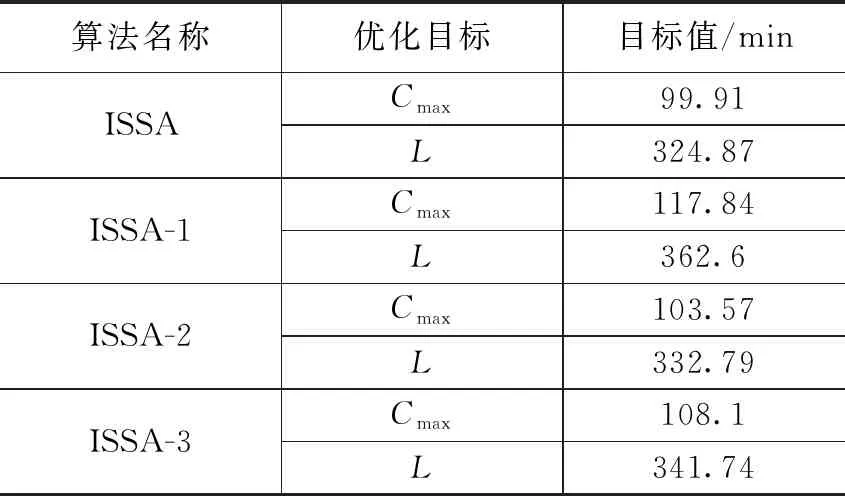
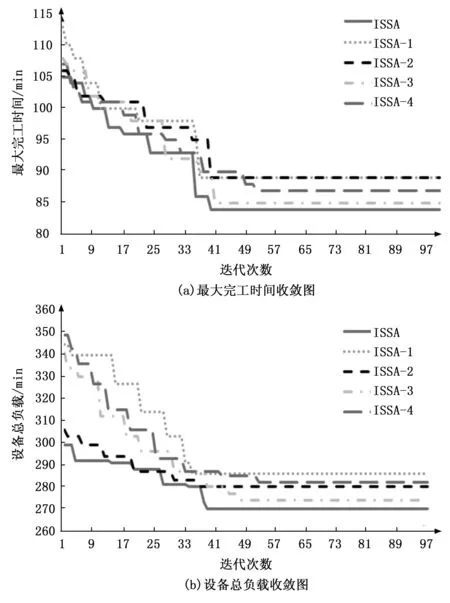
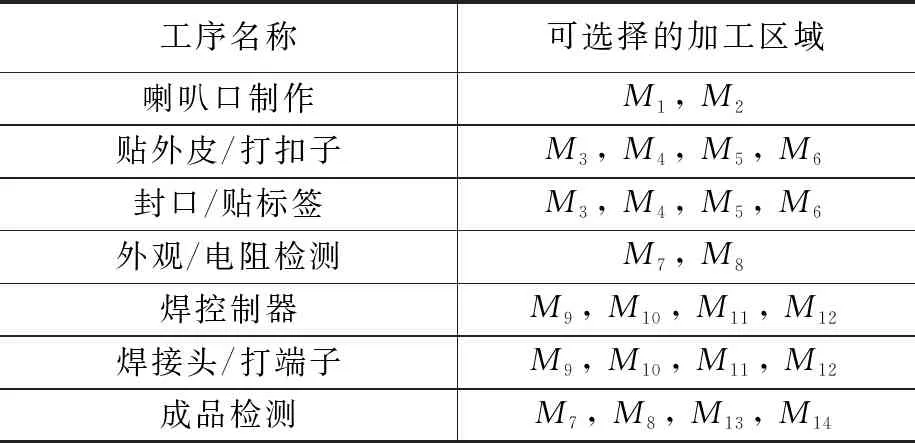
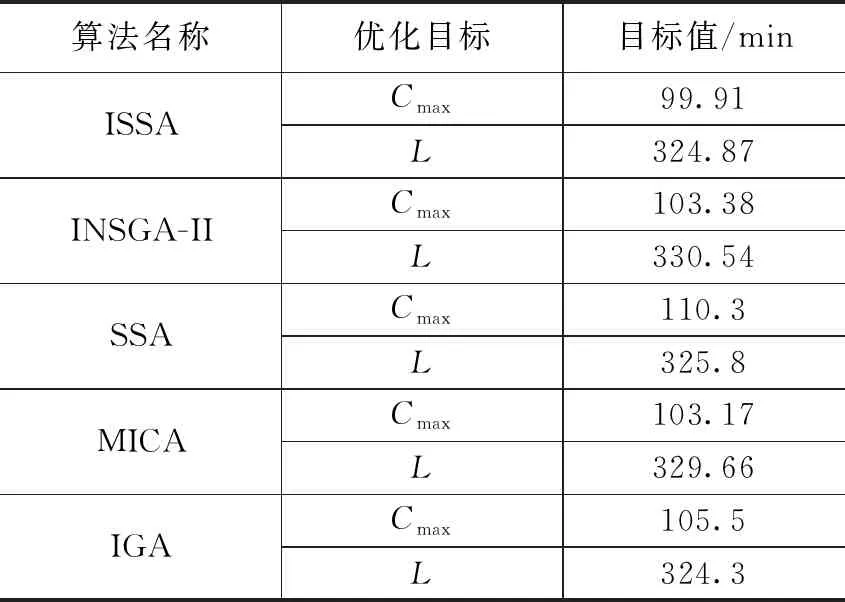
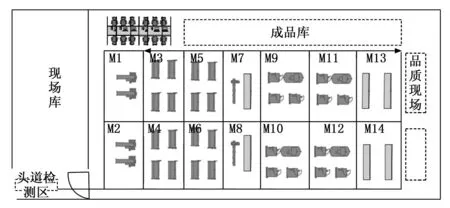
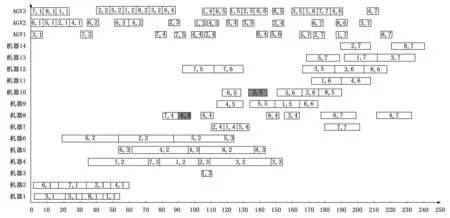
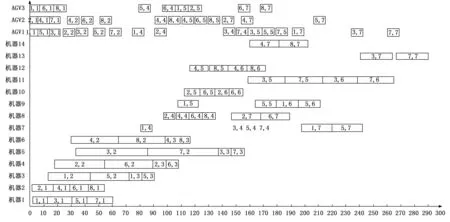
Ei,j,k (6) Te,v,Wi,j-1≤Si,j,k (7) Pei,j-1≤Si,j,k (8) TZe,v,Wi,j+Te,v,Wi,j-TZs,v,Wi,j-Ts,v,Wi,j=Tv,Wi,j (9) Ci=Ei,n,k (10) 其中:式(1)保證機器加工工序的時空唯一性;式(2)表示AGV運輸工件的時空唯一性;式(3)和式(4)確保AGV空載開始時間不早于上一次運輸結束時間而空載結束時間不早于工件的上一道工序的完工時間;式(5)和式(6)確保AGV負載開始時間不早于空載結束時間和Oi,j加工結束時間;式(7)和式(8)表示Oi,j的開工時間不早于負載結束時間和Oi,j-1加工結束時間;式(9)表示AGV完成任務Wi,j所需的時間等于空載時間加上負載時間;式(10)表示工件的完工時間等于最后一道工序結束的時間。 FJSP一般把某個調度指標作為評判調度方案是否合理的標準,常見的調度指標包括訂單的完成時間、機器使用壽命、設備負載均衡等,其中最小化最大完工時間和最小化設備總負載是最常用的評價指標,如式(11)和式(12)所示: f1=Cmax=min(maxCi) (11) (12) 半導體管道加熱器柔性作業車間的生產調度方案決定車間的生產效率及生產成本。不同于傳統的FJSP,還需考慮工件的運輸時間。隨著產業的智能化升級,AGV被應用到車間的配送環節中,承擔工件的運輸任務,AGV成為求解車間生產調度方案的重要約束。 將管道加熱器生產車間抽象為1.2所述數學模型,以最大完工時間代表生產效率,以設備總負載代表生產成本,并考慮實際生產過程中可能出現的撤單、設備故障、新訂單等動態擾動。為求解車間的生產調度方案,可以采取啟發式群智能優化算法[16]。其中麻雀搜索算法于2020 年提出,由于具有搜索穩定、精度高、收斂快等一系列優點,一經提出便被廣泛應用于深度學習、路徑規劃等領域,但在柔性作業車間調度方面應用較少,且存在著很大的優化空間。麻雀搜索算法被廣泛應用于FJSP,但都未能深入討論AGV在FJSP中所起到的約束作用,因此提出一種改進麻雀搜索算法求解AGV、機器雙約束的柔性作業車間調度問題,并使用開源數據集進行驗證。 作為一種群智能優化算法,麻雀搜索算法受自然界動物種群啟發,主要模擬麻雀種群的覓食及反捕食行為。麻雀種群在尋找食物的過程中具備明確的內部分工,覓食能力強的個體被稱為發現者,其余麻雀作為跟隨者共享發現者提供的食物信息。同時,種群中具有警戒者,它們在感知到危險后會發出警報信號,種群會飛行至其他安全區域覓食。在迭代中,發現者的位置更新公式為: (13) 其中:t為迭代次數,Xi,j為麻雀i在j維的解,itermax為最大迭代次數,α為(0,1]內的一個隨機數,ST為安全值,R2是預警值,L是元素為1的d維矩陣,Q是服從正態分布的隨機數。對于跟隨者,其位置更新公式如下: (14) 其中:XP為最優發現者,Xworst則表示全局最差解,A為一個d維矩陣。當i>n/2 時,表明跟隨者i沒有食物,需要飛往其它地方覓食。對于警戒者,其位置更新公式為: (15) 其中:Xbest則表示全局最優解,β為步長控制參數,K為一個隨機數,fi則是當前個體的適應度值,fg和fw分別為當前全局最佳和最差的適應度值,ε為最小的常數。 機器和AGV雙約束的FJSP包含3個子問題:工序分配子問題、機器分配子問題以及AGV調度子問題。其中機器分配子問題是為工序選擇合適的加工機器;工序分配子問題是指確定機器上的工序加工順序,以此確定工序加工起止時間;而AGV分配子問題是為各工序安排適合的AGV,進而確定運輸任務的起點、終點以及運輸時間。通過麻雀個體的編碼去解決機器分配問題和工序排序問題,在解碼過程中通過一種自適應貪心算法求解AGV調度子問題。 合理的編碼規則和解碼方式是求解FJSP的關鍵,模型采取基于工序的二維編碼方式,包括工序向量OS(Operation Sequencing)和機器向量MS(Machine Sequencing)。OS由工件號組成,順序讀取OS,工件的工序數即工件號當前的出現次數,MS從左向右與OS逐一對應,如圖1所示。 圖1 編碼方式 AGV在解碼過程中進行調度,構建一種基于自適應貪心算法的AGV分配策略。解碼過程是順序解碼,當編碼靠后的工件先抵達指定機器時,其需要等待編碼靠前的工件抵達并加工后才能進行加工,這種情況可能造成最大完工時間的整體后移,因此,需要在解碼過程中加入前插判定,對于工序Oi,j和機器M,若滿足以下條件則進行前插。 1)當Oi,j-1同樣是在機器M上加工時,遍歷機器M上已解碼工件集OM,設Om.n和Ox,y是機器M上相鄰的兩道工序,且Ox,y先于Om,n加工,當滿足式(16)時工序Oi,j可以前插置Ox,y和Om,n之間進行加工。 Si,j,M≥Ei,j-1,M&&Sm,n,M-Ex,y,M≥Pi,j,M (16) 2)當Oi,j-1在其他機器上加工時,遍歷機器M上已解碼工件集OM,當滿足式(17)時工序Oi,j可以前插置Ox,y和Om,n之間進行加工。 (Te,v,Wi,j≥Ex,y,M&&Sm,n,M-Te,v,Wi,j≥ Pi,j,M)||(Ex,y,M≥Te,v,Wi,j&&Sm,n,M-Ex,y,M≥Pi,j,M) (17) 2.3.1 初始化種群 種群的初始解質量會直接影響算法的收斂速度和最終解的質量。綜合考慮初始解的多樣性和收斂性,選擇隨機生成和局部貪心選擇兩種方法相結合生成初始麻雀種群,兩種初始化方式各占50%。 兩種方法的工序碼隨機由隨機數排序產生。對于機器碼,隨機初始化可以選擇可用機器集中的任意機器,而局部貪心初始化左至右遍歷工序碼,選擇加工耗時最短的機器,獲得的解具有較小的初始設備總負載。 2.3.2 改進位置更新公式 由于SSA主要用來解決連續優化問題,而FJSP是典型的離散優化問題,直接將式(13)~(15)用于解的更新會產生大量非法解,極大地降低搜索效率,且麻雀搜索算法具有收斂過早、易陷入局部最優等缺陷。因此在SSA的位置更新公式中結合NSGA-II算法,將交叉變異算子和變鄰域搜索應用于麻雀位置更新,提高算法尋優能力。 SSA的尋優能力主要取決于發現者,若發現者陷入局部最優,則算法性能也隨之下降,因此發現者應當具備尋優方式多樣和尋優能力強等特點。為擴大搜索域,將POX (Precedence Operation Crossover)算子和RPX (Random Precedence Crossover)算子[17]引入發現者位置更新,在使用式(13)對工序碼進行更新后,使用式(18)對發現者的位置進行再次更新: (18) 圖2 POX交叉算子 對機器段使用RPX交叉算子,即遍歷父代的機器段,以一定概率交換兩個體中相同工序所選擇的不同機器。Mut()是變異操作,以一定概率采用兩點變異。為了防止出現無效解,在變異后需要對機器碼做修復,若工序Oi,j無法在機器k上加工,則從工序Oi,j的機器集中隨機選一個可用機器。 從式(14)和(15)可以看出警戒者和跟隨者的位置更新均受最差個體的影響,這限制了種群多樣性和種群的搜索范圍,為加強發現者的引導作用,使用交叉變異算子使跟隨者獲取發現者的位置信息,跟隨者的位置更新公式為: (19) 同理,在警戒者進行位置更新后使用變鄰域下降搜索算法對其進行再次更新,公式為: (20) 警戒者可用來突破局部最優,鄰域結構包括:兩點交換鄰域、單點插入鄰域、變異鄰域結構。前兩者可能產生無效解,需要在變鄰域搜索后遍歷并做修復。 2.3.3 基于Patero等級排序 由于算法具備多個優化目標,適應度值是向量而非標量,單一指標無法判斷解的優劣,因此引入Patero支配策略[18]來劃分解的質量優劣。解之間的支配關系反映了兩個解質量的好壞,假設x1,x2是解空間的兩個可行解,解x1生成的方案要優于x2,則稱解x1支配解x2,而x1支配x2的充要條件是任意x1的目標函數小于等于x2的目標函數且存在x1的目標函 數小于x2的目標函數。若x1,x2互不支配,則稱x1與x2無差別。 結合NSGA-II算法的快速非支配排序,根據解的Patero等級和擁擠度進行排序,并依次劃分發現者和跟隨者。在快速非支配排序中,設每個解都有參數S(j)和N(j),其中S(j)是麻雀j支配的解的集合,N(j)是種群中可以支配麻雀j的解的數量。N(j)越小解越優秀,若N(j)等于0,則解j的Patero等級是0,稱解j是最優解。對于同一Patero等級的解,通過擁擠度進行排序,擁擠度的計算采用的Harmonic平均距離[19],某個體的Harmonic平均距離Hdsi定義如式(21),排序步驟如下: 1)計算所有麻雀的N(j)和S(j),k= 1; 2)將所有N(j) = 0的個體存入集合F(k); 3)遍歷F(k)中個體的S(i),將集合S(i)中每個個體的N(j)減1; 4)將F(k)中個體按照擁擠度進行排序,k=k+1; 5)重復步驟2)~4)直到所有麻雀都被排序。 (21) 其中:di,Nm表示與其他個體的幾何距離,Nm表示優化目標數目,在式(19)中表示參與計算的與該個體集合距離最小的個體數量。 2.3.4 精英麻雀策略 改進麻雀搜索算法融合了傳統麻雀算法和NSGA-II搜索算法的特征。在子代更新階段,傳統麻雀算法可能導致父代的優秀個體丟失。而NSGA-II算法在子代更新階段使用二元錦標賽法篩選子代種群,隨著迭代的進行,子代中存在大量近似解,算法陷入局部最優。為使算法在保持種群多樣性的情況下保留父代的優秀個體,引入一個獨立于迭代種群外的精英種群,初始精英種群由初始麻雀種群的最優解集組成,并隨著迭代的不斷更新種群成員。同時,為提高子代種群的搜索質量,選擇精英解加入到發現者中參與迭代。精英種群的更新方法如下: 1)遍歷子代種群,若精英種群中存在一個解支配子代個體,則跳過該個體; 2)若子代個體與精英種群中所有個體均互不支配,將其加入精英種群; 3)若子代個體支配精英種群中一個或多個個體,則子代個體替換精英種群中被其支配的個體; 4)在更新過程中,為防止精英種群中個體越來越多,需設置種群數目上限,并使用擁擠度排序去除所有順序超出上限的解。 2.3.5 自適應種群比例因子 搜索廣度與深度之間的協調對于SSA的性能至關重要。為此,提出自適應種群比例策略。在迭代的早期階段,發現者占大多數,其數目隨著迭代次數的增加而自適應減少,跟隨者的數量自適應增加,從而提高方案的質量。具體公式表示為: (22) pNum=r*N (23) sNum=(1-r)*N (24) 其中:pNum定義為發現者的數量,sNum表示跟隨者的數量,b定義為一個比例因子,σ是一個[0,1]之間的偏差因子,N是總迭代次數,T是當前迭代次數。 使用ISSA (improved sparrow search algorithm)求解柔性作業車間調度方案的流程如圖3所示,具體步驟如下: 圖3 改進麻雀搜索算法流程圖 1)初始化麻雀種群數量、初始發現者、跟隨者、警戒者比例、ST等,按照2.3.1節方法獲取初始解。 2)按照2.3.3節方法劃分種群的Patero等級,將最優解集加入到精英種群。 3)按照式(13)和(16)更新發現者位置。 4)按照式(14)和(17)更新跟隨者位置。 5)按照式(15)和(18)更新警戒者位置。 6)劃分子種群的Patero等級,按2.3.4節方法更新精英種群。 7)若滿足終止條件,輸出精英種群作為最終調度方案集合,否則返回步驟3)。 仿真調度案例使用文獻[20]和文獻[21]中提出的考慮工件運輸時間的FJSP基準實例(數據集下載地址:https://fastmanufacturingproject.wordpress.com)。改進麻雀算法的主要參數包括迭代次數M=100,種群數量N=50,精英種群數量SN= 10,安全閾值ST=0.8,發現者、跟隨者的比例按2.3.5節劃分,警戒者占20%,設存在兩個AGV進行物料運輸。 為驗證改進措施的有效性,分別對比ISSA、離散化SSA、SSA+初始化、SSA+精英策略、SSA+自適應因子5種算法,將5種算法分別命名為ISSA、ISSA-1、ISSA-2、ISSA-3,ISSA-4,其中離散化SSA由2.3.2和2.3.3節組成。為避免偶然性對實驗結果的影響,分別進行20次仿真實驗,對實驗數據取平均值,對比5種算法取得的Cmax和L。 由表2可以看出,ISSA算法所求得的Cmax和L都是最優的,驗證了所提出的4種改進策略的有效性。從ISSA-1、ISSA-2、ISSA-3、ISSA-4的對比數據中可以看出混合初始化機制、精英種群機制和自適應比例因子都對算法尋優有一定效果。其中ISSA-3的尋優效果提升更大,說明精英種群機制對算法的求解質量有較大的提升效果。這是由于SSA在迭代過程中會丟失父代的較優解,導致每輪迭代的最優解集互相之間沒有聯系,局部搜索能力下降。而在設置精英種群且精英種群加入子代選擇后,精英解為種群提供導向,且隨著精英種群動態更新,可有效防止算法陷入局部最優。 表2 案例結果對比表 為探究各優化策略對算法性能的影響,以算例JS1L1為例,5種算法求解算例JS1L1的收斂曲線如圖4所示。采取了混合初始化方法的ISSA-2擁有質量較高的初始解。擁有自適應種群因子的ISSA-4在算法早期獲得較大的發現者比例,提高全局搜索能力,隨著迭代的進行擴大跟隨者的比例,提升算法局部尋優能力,使得種群迅速收斂。而ISSA-3則通過精英種群策略保留并更新每代的最優解集,獲取較強的突破局部最優的能力,其收斂曲線呈階梯型下降。而ISSA算法綜合以上特點,具備最佳的尋優能力。 圖4 算例JS1L1的迭代曲線圖 為進一步驗證ISSA算法的有效性,分別與INSGA-II算法、SSA算法、MICA算法及IGA算法進行對比,結果如表3所示。 表3 管道加熱器的工藝信息表 表3 最大完工時間對比結果 由表3可知,ISSA算法求解出的最優值均達到當前最佳。對于案例JS7L4,其最優值和平均值均遠強于其它算法,表明了ISSA算法在求解較復雜案例時也有著較為突出的搜索性能。同時,ISSA算法的平均解值與最優解值的差距很小,可見算法搜索性能的穩定。圖5為ISSA求解JS7L3算例所獲得的甘特圖。 圖5 JS7L3調度甘特圖 以某公司半導體管道加熱器柔性作業車間為例,研究ISSA在實際生產中的應用。該車間是管道加熱器組裝及后處理車間,主要包括管道外觀修飾、焊接控制器和封頭等工序。車間布局如圖6所示。 圖6 改進后的車間布局圖 對半導體管道加熱器生產車間進行改造,按照功能將原車間劃分為14個加工區域。引入AGV進行區域間的物料運輸,使用改進蟻群算法求解 AGV 在不同區域間的物流時間。以一批包含4種8個工件的訂單加工任務為研究對象,安排其在改造后的車間進行加工。組裝車間主要的加工目標是多品種的半導體管道加熱器,以小管加工為例,其工序以及可選擇的加工區域如表3所示。每個工序可以選擇多個不同機器進行加工,雖然工序相同,但 由于不同品種的加熱器具有不同的尺寸、形狀以及控制器數量,且在加工過程中受工人操作熟練度約束,同一工序在不同工位上加工時有不同的加工時間。 在車間的生產調度中,AGV數量會對調度結果產生較大影響。當AGV數量較少時,無法高效地完成物料運輸,機器大多處在等待工件的狀態,設備利用率較低。當AGV過多時,其相互之間的路徑沖突增多,運輸效率下降,造成生產效率下降,且過多的AGV會增加企業的運營成本,降低企業利潤。 作業車間的現行調度方案為人工實時調度,其調度規則如下:1)在選擇加工順序時,按照工件的工序順序和訂單序號進行調度;2)在選擇機器時,按照訂單序號和機器序號依次安排可用機器;3)若存在多道相鄰工序可在同一機器上加工,則由同一機器完成相鄰工序的加工。調度方案如圖7所示,其最大完工時間是289.9 min,設備總負荷是1 124.3 min。同時,使用改進麻雀搜索算法對同一調度問題進行求解,調度甘特圖如圖8所示,其最大完工時間是242.3 min,設備總負載是1 093.9 min。 圖7 改進麻雀搜索算法調度甘特圖 圖8 人工調度甘特圖 根據圖8可知人工調度方案加工順序并不合理,且各設備負載差距較大,總加工時間較長。雖然簡單明了,但忽略了每個工件之間的加工時長差異。而在小批量、多品種柔性作業車間中,個體之間的加工順序可能相同,但單步工序的加工時間差距較大,人工調度無法獲得高效、低成本的加工方案。使用改進麻雀搜索算法求解的調度方案可先于人工方案47.6 min完成生產任務,效率提升了19.6%,同時其比人工方案減少了30.4 min的設備使用時長。 探究實際的柔性作業車間生產過程,將運輸時間引入傳統FJSP,將AGV作為物流系統的載體,同時提出多種柔性作業車間優化目標,建立更貼合實際的FJSP模型。設計一種二維編碼方法表示調度方案。在解碼過程中使用自適應貪心算法解決AGV分配問題,并提出一種改進麻雀搜索算法獲取較優解。將ISSA算法與NSGA-II算法進行結合,使用交叉變異算子以及變鄰域搜索算法突破局部最優,使用精英種群保存迭代過程中的較優解集。通過多個經典案例測試,結果表明算法在求解靜態及動態調度問題上有很好的效果。 本文提出改進麻雀搜索算法和改進蟻群算法分別求解AGV約束下的多目標FJSP和AGV的路徑規劃問題,此外還對車間的動態擾動做了深入探討,取得了一定成果。 結合某公司柔性生產車間,研究了上述算法的實際生產意義,對原生產車間進行改進以便引入AGV執行運輸任務,使用上述算法生成調度方案,并與車間原生產方案進行對比,驗證了算法的優越性。結合車間的實際擾動事件,驗證了所提方法的可行性。2 改進麻雀搜索算法求解柔性作業車間調度問題
2.1 麻雀搜索算法
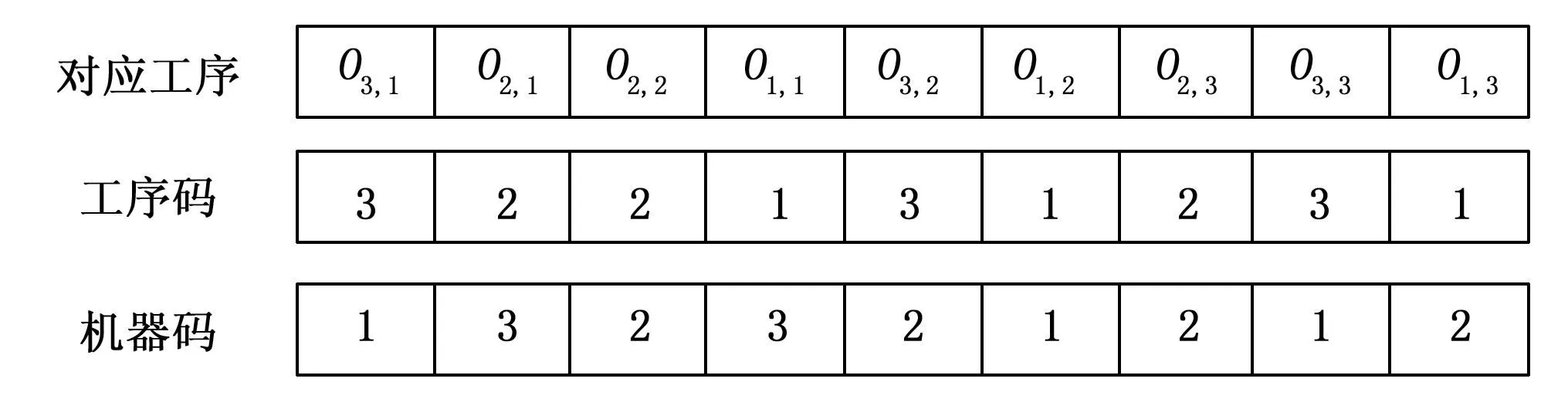
2.2 編碼與解碼
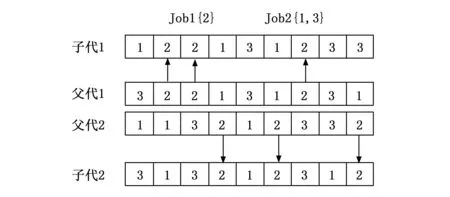
2.3 改進麻雀搜索算法

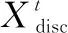
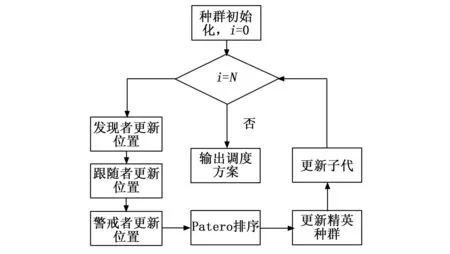
3 算法流程
4 實驗驗證
4.1 仿真實驗

4.2 工廠實例
5 結束語

