結構化學熱點“晶胞計算”的幾何解法

韓建豐　高凌蕊

結構化學部分高考題目考查內容為：①核外電子排布，包括基態（激發態）原子電子排布式（或軌道表示式）、I1（第一電離能）、電負性、元素周期表及周期律等；②分子的結構與性質，共價鍵理論、雜化軌道理論、VSEPR（價層電子對互斥模型）分子空間構型、極性、分子間作用力等；③晶胞結構與性質，包括常見晶體的堆積方式、配位數、晶胞計算、晶體類型及性質比較等。這三個方面在高考題中呈現出“由易到難、層級遞進”特點，晶體結構與性質部分相對而言難度較大。

有關晶體的熱點考查內容為“晶胞計算”，在各地的化學高考中都屬于難點內容。晶胞計算涉及相關內容有：常見晶胞結構特點、晶胞中原子分數坐標、晶胞簡單計算（均攤法、晶胞密度、半徑），高頻考點如圖1所示。

可見晶胞空間結構和微粒間的位置關系是晶胞計算的核心，不妨從原子坐標出發建立空間坐標系，使用幾何知識解決問題。通過遷移“高中數學知識”可以高效快速解決晶胞計算問題。

一、晶胞計算幾何解法模型應用示例

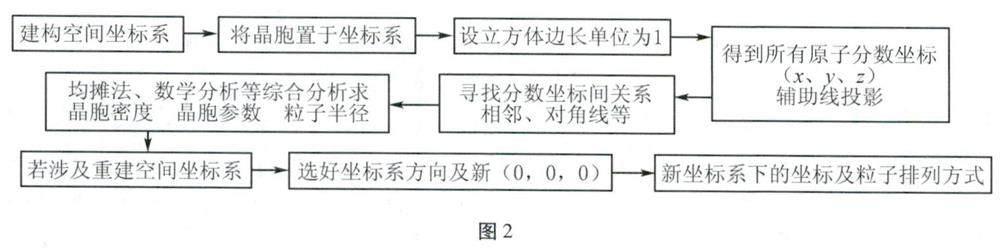
晶胞計算的關鍵在于清晰確定各粒子的空間位置，借助空間坐標系確定原子分數坐標即可形成清晰認知，從而形成“晶胞計算”的幾何解法模型，如圖2所示。

建立模型讓晶胞計算的化學問題變為簡單數學問題，培養學生跨學科綜合素養、通過幾何推理和計算解決化學“難點”的能力。探尋“晶胞計算”考查方式和幾何解法，可逐步形成模型認知，使學生具備此類問題的解題思路、方法、技巧和信心。學生的幾何解法模型建立后應通過理解、記憶、掌握、運用模型認知解題，在運用中夯實基礎提升思維水平。

晶胞計算問題作為部分學生化學學習的“難點”，應用“幾何計算”可以突破，而用到的數學知識僅為初中水平。

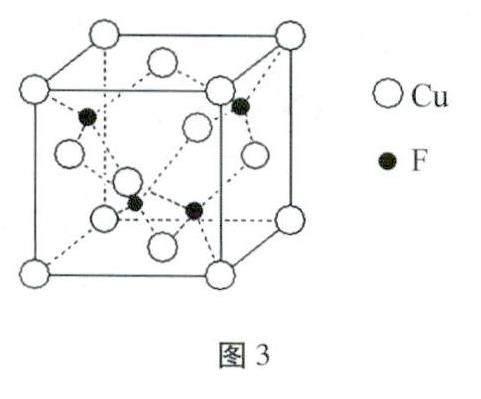
例題1 Cu+和F-形成的晶胞結構如圖3所示，其晶胞密度為a（g／cm3），求陰陽離子最近距離（單位pm）。

解析 應用幾何解法可將粒子位置清晰可視化。

[幾何解法：確定粒子位置]

可建立三維空間坐標系。如圖4所示。

晶胞是無隙并置的，在化學中認為8個頂點坐標均為（0，0，0）。但若只從單個品胞的數學角度（按照空間直角坐標系規則）則可設立方體邊長為1，在空間坐標系中可確定圖4中的8個頂點坐標：（0，0，0）、（1，0，0）、（1，l，0）、（0，1，0）、（0，0，1）、（1，0，1）、（1，1，1）、（0，1，1）；