高中物理教學(xué)中斜拋運(yùn)動(dòng)及其應(yīng)用探析

王小平

摘要：斜拋運(yùn)動(dòng)在生活中隨處可見，比如扔鉛球、扔石頭以及導(dǎo)彈的發(fā)射等.文章利用水平和豎直方向的分解以及斜交方向的分解對(duì)斜拋運(yùn)動(dòng)進(jìn)行研究，然后結(jié)合例題給出斜拋運(yùn)動(dòng)的應(yīng)用探析.

關(guān)鍵詞：高中物理；斜拋運(yùn)動(dòng)；應(yīng)用探析

中圖分類號(hào)：G632文獻(xiàn)標(biāo)識(shí)碼：A文章編號(hào)：1008-0333（2024）12-0077-03

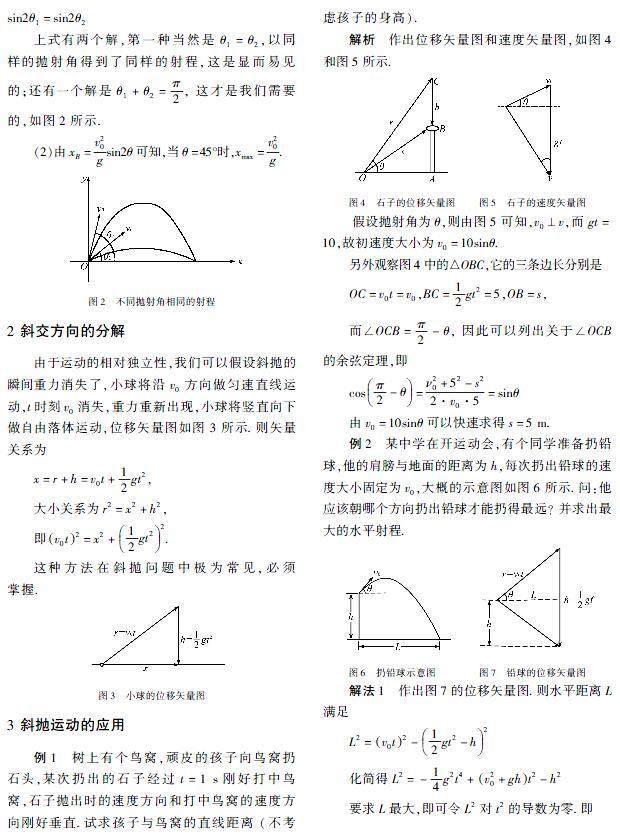
小到運(yùn)動(dòng)會(huì)的扔鉛球，大到洲際導(dǎo)彈的發(fā)射，都需要研究斜拋運(yùn)動(dòng)的規(guī)律.在水平地面O點(diǎn)以速度v0斜向上方扔出鉛球，鉛球的軌跡如圖1所示，最高點(diǎn)是A點(diǎn)， 落地點(diǎn)是B點(diǎn).下面對(duì)斜拋運(yùn)動(dòng)進(jìn)行分析，并給出其應(yīng)用.

1 水平和豎直方向的分解

和平拋運(yùn)動(dòng)的處理一樣，最常見的分解方式就是沿水平和豎直方向分解.建立如圖1所示的O-xy坐標(biāo)系，分解初速度為v0x=v0cosθ和v0y=v0sinθ，由于只有-y方向存在加速度ay=-g，故t時(shí)刻的兩個(gè)分速度為

vx=v0cosθ①

vy=v0sinθ-gt.②

t時(shí)刻的兩個(gè)分位移為

x=v0cosθ·t③

和y=v0sinθ·t-12gt2④

①～④式給出的是拋體運(yùn)動(dòng)的運(yùn)動(dòng)方程，這些方程包含了拋體運(yùn)動(dòng)的全部信息，一切待求的物理量均可從這些方程中得到[1].

比如圖1中的最高點(diǎn)A，它的特點(diǎn)是vy=0，由②式可得運(yùn)動(dòng)時(shí)間tA=v0gsinθ， 再把tA代人④式，可得A的高度（即射高） 為H=ν20sin2θ2g.

再看B點(diǎn)，它的特點(diǎn)是y=0， 由④式可得運(yùn)動(dòng)時(shí)間為tB=2v0sinθg， 代人③式可以算得

xB=vBtB=v0cosθ·2v0sinθg=v20gsin2θ.

我們把xB稱作斜拋運(yùn)動(dòng)的射程， 它是一個(gè)很重要的物理量， 有必要詳細(xì)討論一下.

（1）同樣大小的初速度，如果選擇不同的拋射角有可能得到相同的射程.

根據(jù)射程公式可得v20gsin2θ1=v20gsin2θ2，即sin2θ1=sin2θ2

上式有兩個(gè)解，第一種當(dāng)然是θ1=θ2，以同樣的拋射角得到了同樣的射程，這是顯而易見的；還有一個(gè)解是θ1+θ2=π2， 這才是我們需要的，如圖2所示.

（2）由xB=v20gsin2θ可知，當(dāng)θ=45°時(shí)，xmax=v20g.

2 斜交方向的分解

由于運(yùn)動(dòng)的相對(duì)獨(dú)立性，我們可以假設(shè)斜拋的瞬間重力消失了，小球?qū)⒀豽0方向做勻速直線運(yùn)動(dòng)，t時(shí)刻v0消失，重力重新出現(xiàn)，小球?qū)⒇Q直向下做自由落體運(yùn)動(dòng)，位移矢量圖如圖 3所示.則矢量關(guān)系為x=r+h=v0t+12gt2，

大小關(guān)系為r2=x2+h2，

即v0t2=x2+12gt22.

這種方法在斜拋問題中極為常見，必須掌握.

3 斜拋運(yùn)動(dòng)的應(yīng)用

例1樹上有個(gè)鳥窩，頑皮的孩子向鳥窩扔石頭，某次扔出的石子經(jīng)過t=1 s剛好打中鳥窩，石子拋出時(shí)的速度方向和打中鳥窩的速度方向剛好垂直.試求孩子與鳥窩的直線距離 （不考慮孩子的身高）.

解析作出位移矢量圖和速度矢量圖，如圖4和圖5所示.

假設(shè)拋射角為θ，則由圖5可知，v0⊥v，而gt=10，故初速度大小為v0=10sinθ.

另外觀察圖4中的△OBC，它的三條邊長(zhǎng)分別是

OC=v0t=v0，BC=12gt2=5，OB=s，

而∠OCB=π2-θ， 因此可以列出關(guān)于∠OCB的余弦定理，即

cosπ2-θ=ν20+52-s22·v0·5=sinθ

由v0=10sinθ可以快速求得s=5 m.

例2某中學(xué)在開運(yùn)動(dòng)會(huì)，有個(gè)同學(xué)準(zhǔn)備扔鉛球，他的肩膀與地面的距離為h，每次扔出鉛球的速度大小固定為v0，大概的示意圖如圖6所示.問：他應(yīng)該朝哪個(gè)方向扔出鉛球才能扔得最遠(yuǎn)？ 并求出最大的水平射程.

解法1作出圖7的位移矢量圖.則水平距離L滿足

L2=v0t2-12gt2-h2

化簡(jiǎn)得L2=-14g2t4+v20+ght2-h2

要求L最大，即可令L2對(duì)t2的導(dǎo)數(shù)為零.即

dL2dt2=-12g2t2+v20+gh=0

故可知當(dāng)空中的運(yùn)動(dòng)時(shí)間為t2=2v20+ghg2時(shí)，L有極大值，即

Lmax=v0gv20+2gh

可得拋射角θ的正切值為

tanθ=12gt2-hv0t=v0v20+2gh.

解法2作出鉛球落地瞬間的速度矢量圖，如圖8所示.它的三條邊分別是初速度v0，與水平線的夾角為θ，末速度v，與水平線的夾角為β和豎直方向的速度gt.

則這個(gè)矢量三角形的面積為

s=12·gt·v0cosθ

由于水平射程L=v0cosθ·t，比較L和s，發(fā)現(xiàn)它們成正比，故有

s=12gL

也就是說當(dāng)面積s越大，水平射程L也是越大的.那么怎么確定s的最大值呢？下面再用三角形面積的第二種計(jì)算方式得到

s=12v0·v·sin（θ+β）

其中，落地速度v的大小是恒定的，由機(jī)械能守恒有

12mv2=12mv20+mgh

即可得v=v20+2gh.

那么只要v0和v所夾的角度為直角，則此面積取得極大值，對(duì)應(yīng)的L當(dāng)然也就是最大了.此時(shí)有tanθ=v0v20+2gh，Lmax=v0gv20+2gh

解法3水平和豎直方向的分解，則有

x=v0cosθ·t①

-h=v0sinθ·t-12gt2②

可以先從②式解得t的表達(dá)式，再代入①式， 進(jìn)而得到x=x（θ），但這個(gè)過程太過復(fù)雜，下面換一種方法進(jìn)行計(jì)算.

由①式得t=xv0cosθ， 代入②式可得

-h=x·tanθ-gx22v201+tan2θ，

整理為關(guān)于tanθ的一元二次方程，即

gx22v20tan2θ-xtanθ+gx22v20-h=0.

最遠(yuǎn)時(shí)對(duì)應(yīng)θ取重根的狀態(tài)，即要求△=0，此時(shí)水平位移最大，所以

x2-4·gx22v20·gx22v20-h=0.

計(jì)算得xm=Lmax=ν0gv20+2gh，

相應(yīng)的角度滿足tanθ=v0v20+2gh.

4 結(jié)束語

處理拋體運(yùn)動(dòng)的基本思路，首先根據(jù)實(shí)際情況選擇合適的分解方式列出基本式子，然后觀察特定位置的運(yùn)動(dòng)學(xué)特點(diǎn)來輔助求解[2].數(shù)學(xué)上的要求是需要熟練掌握及應(yīng)用三角函數(shù)的倍角公式、和角公式、輔助角公式以及和差化積、積化和差等公式.

參考文獻(xiàn)：

[1]?吳曉松.斜拋運(yùn)動(dòng)的三個(gè)有趣問題[J].中學(xué)物理教學(xué)參考，2023，52（04）：37-38.

[2] 鄭金.探究一道斜拋運(yùn)動(dòng)難題的多種解法[J].物理教學(xué)，2022，44（01）：47-50.

［責(zé)任編輯：李璟］