基于多波束探測系統的海底地形測量

薛陽 張超 董雁南 詹華明

關鍵詞： 多波束 海底地形圖 三角網 規則網 精度評定

中圖分類號： P229 文獻標識碼： A 文章編號： 1672-3791（2024）01-0001-04

海底地形測繪對于海洋開發、海洋工程建設以及海洋環境模擬具有重要意義。隨著計算機技術、地理信息技術以及圖像處理技術的飛躍式發展，海底地形三維可視化成為熱點研究課題。杜躍等人［1］采用多波束的方法對海底復雜地貌進行識別，并通過濾波算法將波束傳播噪聲剔除，實現了復雜海底地貌的識別；馬鄭海等人［2］為提高水下測量的精度，采用多波束開展水下地形數據測量與模型建立，并在長江荊門江一段進行試驗，結果表明：相對于傳統測量技術，多波束水下測量精度更高；余啟義等人［3］對海島停泊水域、回旋水域水下地形進行測量，通過內外符合精度檢測，結果表明SeaBat T20-P 多波束測深系統可高精度地獲取水底地形數據。

1 多波束系統

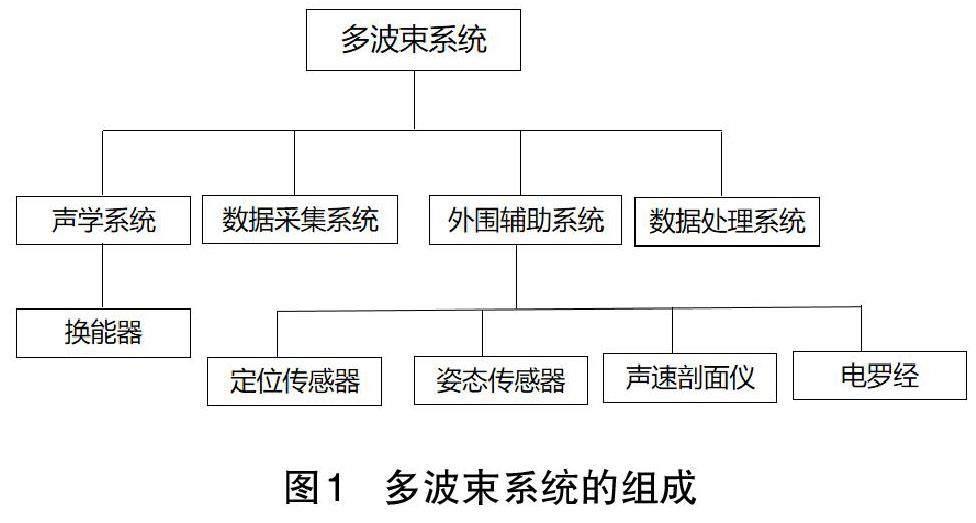
多波束系統是探測海底地形的專業測量系統，通過向海底發射聲波信號，并接收從海底反射上來的回波，通過計算聲波傳輸的時間，計算船底到海底的距離［4］。多波束系統通過向海底發射多條聲吶，可以獲得與船航線相垂直的多個點的水深值，并獲得一條具有寬度的水深帶，而多條水深帶將整個區域的海底覆蓋，形成海底地形數據。多波束聲吶系統主要由4 個部分組成，分別是聲學系統、數據采集系統、外圍輔助系統以及數據中心處理系統［5］，具體如圖1 所示。

1.1 工作原理

多波束聲吶系統的兩組換能器具有正交的特性［6］，可以在同一時刻發射多條波束，通過扇形的波束面記錄對水底進行掃描的數據，再通過接收觸底反饋的波束計算水深。換能器在測量船的底部，發射線呈扇面的形狀向下發射波束，接收器將接收的聲波轉換成數字信號，通過不同角度的聲波反射時間計算水深。

在測量過程中，聲吶直接計算的水深值存在各種系統誤差，不能直接反映具體水深，因此需將各類改正值添加到測量值中進行改正，多波束的測量水深值如式（1）所示。

1.2 數據處理

多波束測量系統可獲得的數據包括水深值、位置坐標數據、測量時的姿態數據以及聲速剖面數據等，為獲取高精度的三維地形數據，需要對獲取的原始數據進行預處理。在測量船工作過程中，由于儀器設備自身存在的系統誤差與測量環境的影響，測量獲取的數據中難免會存在各類誤差和噪聲，導致地形測量不準確。因此，在進行地形建模時需要剔除各類噪聲，并對數據進行糾偏。

1.2.1 數據讀取

讀取原始數據并進行格式轉換，滿足數據處理軟件的格式要求，對數據的來源進行注釋。

1.2.2 聲速剖面數據改正

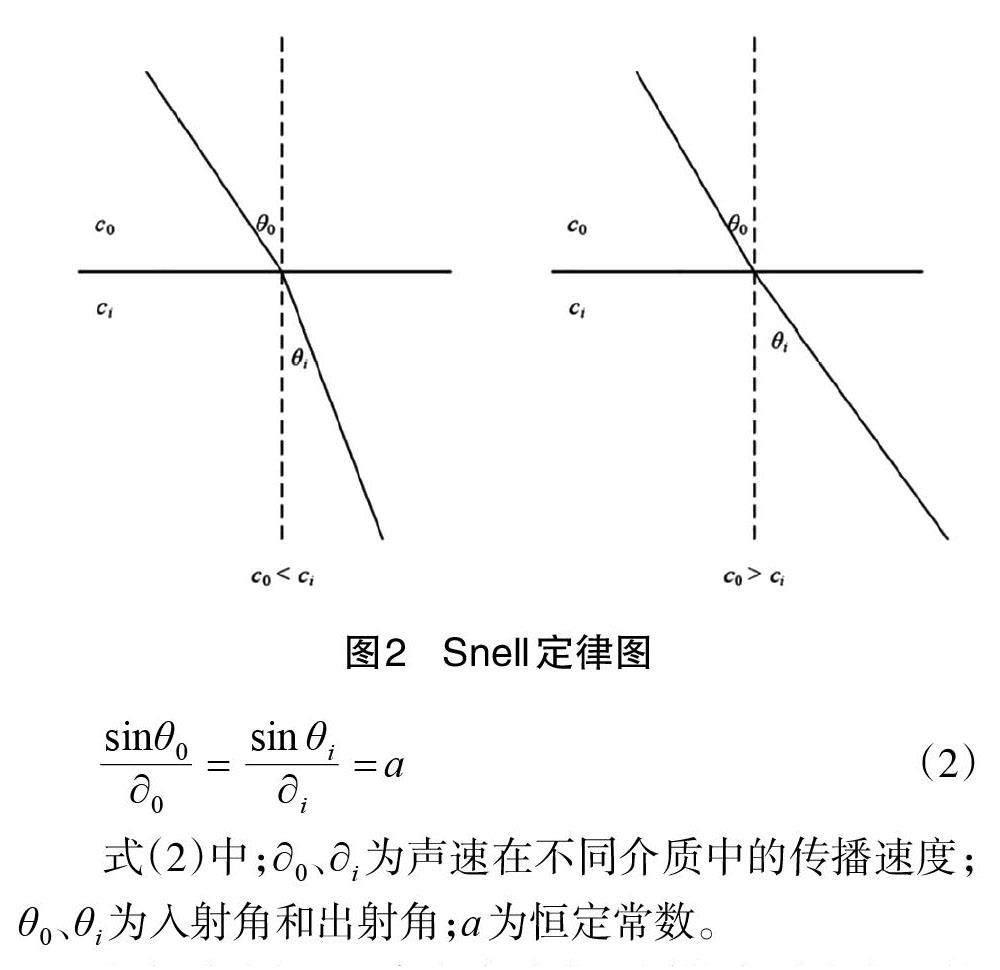
海水的溫度、鹽度等因素對聲波的傳播影響較大。在同一位置，海水的深度不同對聲波的影響不同，因此多波束在海水中的傳播線路并不是直線［7］。中間的波束為垂直向下，可看作一條直線，對于超過45°的波束，聲波在傳播過程中逐步產生了偏差，發生了折射現象［8］，成為一條曲線。因此，需要根據聲速剖面對聲線進行跟蹤，計算新的測深值。隨著海水深度的增大，聲速發生的變化也越大，若只考慮聲速在垂直面上發生的變化，則可采用聲速垂直分層模型進行修正。聲速剖面是分層模型的關鍵，在聲吶測深系統工作時，聲速剖面儀也開始對聲速進行監測。在模型匯中，聲速符合斯涅爾定律（Snell's law）如圖2 所示。

根據式（2）可以求出聲波在不同的介質中實際的傳播速度，從而可以得到真實的水深值。

1.2.3 定位數據改正

測量船在航行過程中通過接收GNSS 信號進行精確的定位，由于大面積水域的電磁信號在傳播過程中存在誤差，因此需要對定位數據進行編輯，主要是剔除跳點數據并刪除噪聲點。工作人員可對因刪除差異點造成的定位信息不連續現象進行點位數據內插，獲取測量時具有相同間隔的連續定位信息，最終測量定位數據將以一系列相同間隔的點位數據表示。

1.2.4 姿態信息處理

姿態數據是指聲吶系統在發射或接收聲吶信息時所處的自身狀態，包括各個方向的傾斜角度。在測量過程中，由于海浪、海風等因素的影響，聲吶系統不可避免地處于搖擺的狀態。因此，在數據解算過程中要修整姿態信息，加入旋轉角修正系數，補償船體姿態引起的測量誤差。

1.2.5 潮位差修正

測量得到的數據是指換能器到海底的水深，也就是獲取的高差數據，因此需要將水深轉換到同一坐標系下的高程系統中，這就需要查閱測量時所在海域空間與根據測量的時刻計算的潮位資料，對測量數據進行潮位數據改正，得到正常的高程信息。

1.2.6 深度數據修正

海底地形的三維模型建立離不開準確的深度數據，而深度數據的精確度直接影響地形的精度。測量獲得的水深數據存在很多假信息與噪聲值，影響后續地形數據的搭建，因此需要對深度數據進行預處理，識別假信息并刪除噪聲點，得到精度較高的深度數據。

1.2.7 數據整理

將水深值、位置坐標數據、測量時的姿態數據、聲速剖面數據以及其他改正數據等所有參數歸算到最后的數據計算中，得到同一坐標系統中海底的精度較高的高程信息。

2 海底地形建模

2.1 規則格網法建模

在進行格網內插計算時，可設定格網單元的大小。根據測量要求的精度進行選擇，格網間距較大，計算速度快，但地形表示不夠精確，不能準確表達細微處的地形起伏。而格網太小，單元間距小，容易造成格網網點附近無測量值，內插時易產生錯誤，并且計算量大。因此，綜合獲取的數據與精度要求對格網單元大小進行設定。本文設置格網單元大小為0.5 m×0.5 m，格網大小為110 列×14 行，分別采用克里金法、反距離加權法以及自然鄰點差值法進行建模，結構如圖3 所示。

根據圖3 所示的3 種不同規則格網發地形建模圖可以看出，反距離加權插值法要比其他兩種方法建立的模型效果更好，克里金法和自然鄰點差值法對條帶的邊緣區域地形進行了較為明顯的拉伸。在建模時間上，反距離加權法用時最短，為3.56 min；克里金法用時接近，為3.86 min；自然鄰點法用時最長，為7.52 min。

2.2 Delaunay 三角網建模

傳統的三角生長法在計算形式上較為簡單，但是需要大量的運算時間，故在此基礎上對該算法進行優化成為眾多學者的研究對象。研究者提出一種更加優化的合并算法，該算法將分治療算法與逐點插入算法相結合，實現了算法的優化和互補。具體思路為以下幾個方面。

（1）將數據點集按照分算算法的方式展開分割處理，按照點的橫坐標和縱坐標分別進行排序形成點集，然后依照點的閾值分割為兩個類似的子集。

（2）采用凸殼算法對點的橫縱坐標分別提取最大值和最小值，提取的點作為初始凸殼，通過遞歸函數將剩下的點連接為完整的凸殼。將最小的x 值或者最小的y 值的點坐標讀入凸殼點集，然后將起始點找到凸點連接為三角形，歷遍所有的點，實現三角網的建立，如圖4 所示。

（3）在初始三角網的基礎上，通過數據內插將凸包內的點都插入到三角網中，生成新的三角網。插入的運算方法需滿足Delaunay 三角網特征。合并子三角網直到迭代至最后的頂點位置。

Delaunay 三角網直接用采集的離散數據點作為三角形的三個頂點，與規則格網的內插數據相比，其精度相對更高，可較好地對地形的起伏特征進行表示。由于數據量較大，局部生成的三角網也比較復雜，如圖5所示。

本文采用合成算法對數據進行處理，可節省大量的計算時間。對比傳統的逐點插入法與合成算法的點位插入法，通過構網時間對比二者的計算速度，如表1所示。

從表1 中可以看出，合成算法的效率要優于傳統構網算法，在進行大量離散點計算時可表現出極大的優越性，節省大量的數據處理時間。

通過合成算法處理獲取的水深點，構建海底三維地形模型，相比于逐點內插算法獲得的三維模型的精細程度更高，細節處表現更加精準，如圖6 所示。

3 精度評定

對規則網法的3 種建模方式與合成算法的建模精度進行評定，采用點位中誤差進行點位精度評價，中誤差計算公式如下：

式（3）中：H_i?為模型內插點的水深值；S_i?為測量獲取的點的水深值；n為檢測點數。

在模型中采取20 個水深點進行中誤差檢測，計算4 種方法得到的中誤差如表2 所示。

從不同的地形圖建模方法中的誤差對比可看出，4種建模方式的中誤差值均滿足海底地形圖測量相關規范精度要求，Delaunay 三角網精度相對更高。

4 結語

多波速測量系統具有高精度、覆蓋面積廣、分辨率高的特點，是海洋地形測量的主要測量儀器設備。本文詳細研究了多波束測量系統的測量工作原理，分析測量數據具有顯著的大數據量、高密度、離散性等主要特點，并對數據處理流程進行詳細闡述。通過采用規則網法與Delaunay 三角網建立海底三維模型，得出Delaunay 三角網建立模型速度更快，細節展示更精準的結論。最后，通過不同建模算法的坐標中的誤差對比可知，Delaunay 三角網建模精度更高。