利用提問法促進學生思維發展

陳萬軍

摘要：提問貫穿課堂教學的始終，在課堂教學中起到至關重要的作用。本文結合教學實踐，從分析并確定學習目標、創設合理的問題情境、把控問題的數量與質量、找準提問時機、設計學生反思環節五個方面入手，提出有針對性的提問策略，以此來激發學生的思維，提升學生的思維能力。

關鍵詞：提問教學思維問題情境

引言

“學起于思，思源于疑。”提問貫穿課堂教學的始終，有效的提問對教學質量的提高和學生思維的發展至關重要，日本著名教育家齋滕喜甚至認為提問是教學的生命。但目前的小學數學教學實踐中，提問仍存在諸多問題：提問偏離教學目標；提出的問題過易或過難，缺乏層次性、深刻性、啟發性；提問過密或過散，重難點不夠突出，達不到訓練學生思維的目的；把握不好提問的時機，導致學生的思維混亂；等等。提問要注意哪些方面？如何有效提問？這是值得深思的問題。

一、分析并確定學習目標

教師必須了解學生的起點能力和學習狀態，進入新的學習主題時，學生的學習習慣、學習方式、知識儲備和技能對新主題學習的成敗起著重要作用。教師在設計問題前，應對所制定的學習目標中知識技能、數學思考、問題解決、情感態度的各組成部分進行分析。基本步驟包括確定學生原有的知識基礎，分析學生的起點能力。了解學生情況的方法很多，作業、測驗、提問和觀察學生的反應都可以。學習目標的分析與確定是課堂提問的起點。

【例一】在“負數的初步認識”教學中，學生已有知識基礎包括自然數和自然數的大小比較，并且學生在生活中認識了諸如溫度計、方向等具有相反意義的量。學生要完成學習任務，必須達到以下四個目標：第一，會正確地讀、寫負數；第二，在生活情境中，經歷數學化、符號化的過程，體會負數的作用；第三，感受正、負數和生活的緊密聯系，培養應用數學的意識；第四，能夠判斷正負數的大小，認識數軸，體會數形結合的思想。因此教學中可以設計這樣幾個問題：什么是負數？負數和正數有什么區別和聯系？為什么引入負數？（負數有什么用？）

二、創設合理的問題情境

創設問題情境的目的在于激發學生的學習興趣，使其產生積極的情感體驗，改變學生已有認知結構，引發學生積極思考。教師要選擇有效的情境，既要關注現實生活，讓情境具有廣度，也要關注教學的目標體系，讓情境具有深度。因此，教師要充分挖掘教材資源，注重以學生熟悉的感興趣的內容為載體，引導學生積極思考，使學生進入“憤悱”的心理狀態。

【例二】我在執教“萬以內數的大小比較”時，出示一張本人登山的照片。師：“我在做什么？”生：“登山。”師：“是的，這座名山高兩千多米，是五岳之一，你們知道它是什么山嗎？”隨即展示五岳的海拔高度信息：東岳泰山1532米，西岳華山2160米，南岳衡山1290米，北岳恒山2017米，中岳嵩山1440米。學生紛紛猜測照片上是什么山。有人說是華山，有人說可能是恒山，還有人說一定不是泰山、衡山和嵩山。我急忙追問：“為什么？”生：“老師剛才說這座山有兩千多米，而這幾座山還沒有達到兩千米呢！”師：“好！我再告訴你們一個條件，它是五座山中最高的。”學生開心地說：“華山。”

在這個教學片段中，我成功創設了登山的情境，比較了華山在“五岳”中的高低，進而學習“數的大小比較”，極大地調動了學生的積極性，激發了學生的數學思維。

【例三】在“角的認識”中，教師提出了這樣的幾個問題：生活中什么物品上有角？能不能把你頭腦中所想的“角”畫出來？其中有哪些是真正的角？你所畫的角有哪些不同？如何在紙上畫一個和黑板上一樣大小的角？角的大小和什么有關？

教師從數學現實出發，以“什么是數學上的角？什么是數學上的角的大小”創設問題情境，成功調動了學生原有經驗和新知識的矛盾，找到新知識的“生長點”，讓學生想得更清晰、更全面、更深入、更合理。

三、把控問題的數量與質量

要做到這一點，必須根據學習內容、學習程度、學習時間給學生設計相應的問題坡度。問題不能過于寬泛而使學生找不到思維的切入點，也不能承載太多的內容、太重的任務，導致思維能力很難提高。應該聚焦幾個核心問題，讓學生深入思考，表面上學得少而慢，但思考的方法豐富了，思維能力也提高了。因此，問題不應太多太細，而應努力做到“少而精”，給學生獨立思考提供充足的時間和空間。要在學生思維的“最近發展區”內提問，即問題的難易要適當，符合大多數學生的需要，使學生“跳一跳夠得著”，鍛煉學生的思維能力。

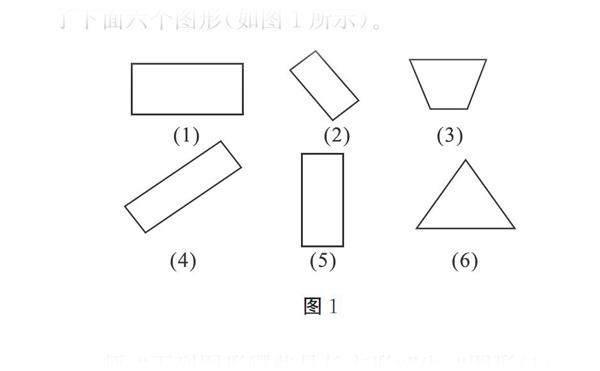
【例四】在三年級上冊“長方形和正方形的認識”的教學中，由于學生在一年級下冊已經直觀地認識了長方形，為了更好地探究長方形的特征，教師展示了下面六個圖形（如圖1所示）。

師：“下列圖形哪些是長方形？”生：“圖形（1）（2）（4）（5）都是長方形。”師：“那么，它們有什么共同的特征？”教師的追問過于寬泛，沒有對長方形邊和角區別于其他圖形的關系作任何說明，而且“什么是圖形特征？怎樣得到特征？”這些對于學生來說很陌生。如果教師追問“長方形的邊長之間有什么關系？四個角都是什么角？”，又過于具體，思考力度不夠，“功利”而且膚淺。我們可以這樣設計追問：“圖形（3）和（6）為何不是長方形？”通過比較，學生得知圖形（3）的四個角不是直角，圖形（6）只有三條邊。這能夠引發學生對長方形的邊和角的思考，進而使其掌握長方形的特征。

除此之外，教師還要根據當前所學知識的生成發展設置問題，引導學生逐步深入，直至得出結論。

四、找準提問時機

教學過程是動態生成的過程。超前的提問，會導致學生思維混亂，失去思考的興趣；而滯后的提問，會使學生輕易地找到答案，這樣的提問因缺乏思維深度而變得沒有意義。這就需要教師找準提問時機。

（一）在學生的疑惑處提問

教學中，教師要善于引導學生進入“憤悱”狀態。學生有了疑問，就會產生求知欲。

【例五】在“年、月、日”的教學中，教師這樣導入：今年小明已經10歲了，從出生到今年小明的媽媽卻只過了8次生日，請大家想一想，小明的媽媽今年是幾歲？學生議論紛紛，頓生疑竇。這時，教師說：“你們想知道小明媽媽是多少歲嗎？學了這節課你就明白了。”短短數語，使學生探索的欲望油然而生，激活了課堂的氣氛，為上好本節課開了個好頭。

（二）在新舊知識的聯系處提問

學生學習新知識需要原有知識的支撐，原有知識可以作為學習新知識的起點。提問要充分利用學生原有經驗，把新知識放在原有知識的背景中去思考。鋪設好“認知的橋梁”，促進新的知識的滲透和遷移，建立完整的認知結構，使學生更全面地理解新知識。

【例六】在蘇教版數學六年級下冊“比例”單元的學習中，教材通過對一張照片的兩次展示，引出這樣的一個問題：“放大前后，照片的長有什么變化？寬呢？”教師希望學生能積極探究，發現規律。但教學中，學生一直忙于計算，缺乏積極的思維活動。

為了給學生的思維活動提供足夠的時間和空間，應先引導學生認真思考這樣一個問題：如何判斷兩個圖形的形狀一致？如果學生覺得難度較大，可以提出以下問題：在“放大”與“縮小”的情況下，圖形中有哪些因素發生了變化，又有哪些特征保持不變？

（三）在教學環節的關鍵處提問

“關鍵處”指教學目標中的重點、難點，有“牽一發動全身”的作用。

【例七】在“百分數的意義”的教學中，重難點是百分數與分數和小數的區別。百分數與學生之前學習的自然數、小數的意義有著明顯的區別，是表示兩個數量之間關系的數。教師需要設計問題，促使學生從“關系”出發認識百分數。

問題1：說一說生活中出現的百分數的意義。

問題2：辨一辨百分數是用什么形式表示的。

問題3：想一想什么是百分數。

問題1讓學生知道百分數很特殊，它和兩個數量有關。問題2將學生的認識又推進了一步，讓學生體會到百分數是表示兩個數之間比的關系。問題3讓學生思考百分數的意義，理解百分數表示一個數是另一個數的百分之幾，又叫百分比，或百分率；知道它只是表示兩者之間的關系，是一種比率的關系。通過解決以上這些問題，學生的思維得到啟發。

（四）在學生思維的瓶頸處提問

學生在學習的過程中，難免受已有經驗的影響，不能深層次地思考，從而出現思維的瓶頸，這時就要老師給予適當的點撥。

【例八】在練習課中，有這樣的一道練習題：林美花和林美華是一對孿生小姐妹，誰的名字筆畫多，多幾畫？

看到這道題目，學生們紛紛拿起筆，認真地數林美花和林美華的名字的筆畫。過了很長時間，學生們紛紛列式：24-23＝1（畫）。此時，老師適時提問：“有沒有其他的方法？”學生們時而陷入思索，時而相互討論。一會兒，有學生列出這樣的式子：7-6＝1（畫）。老師適時追問：“為什么這樣列式？”學生說：“因為他們名字的前兩個字是相同的，所以只要比較花和華的筆畫數就可以了。”這時，又有學生說：“只要比較‘艸和‘十就可以了，所以可以列式：3-2＝1（畫）。”

五、設計學生反思環節

反思是學習過程的一個再概括環節，是對解題過程的整理，以及基礎知識、數學思維方法的歸納總結，也是對不同解題思路的比較和優化。因此，在解決問題之后，教師要適時引導學生對解題過程和方法積極反思，通過回顧解題過程，反思解題方法，感悟數學思想，使思維更有深度。

【例九】在五年級上冊“多邊形的面積”這一單元的教學中，教師就組織回顧反思，引導學生深化對轉化的數學思想的認識和體驗。

在學習了梯形的面積計算方法后，可以讓學生反思以下問題：

（1）在推導平行四邊形、三角形和梯形的面積公式時，都應用了什么思想？在思路上有什么相同的地方，又有什么不同的地方？

（2）在推導三角形和梯形的面積公式時，是否還有別的方法？有的話，比較不同的推導方法，分析其特點。

（3）三角形和平行四邊形是否可以想象成特殊的梯形？它們的面積是否可以用梯形的面積公式來算？

因為反思是在已有實踐的基礎上進行的學習活動，所以學生對問題所涉及的知識、思想和方法的領悟會更深刻。亞里士多德說：“創造性思維就是從疑問和驚奇開始的。”敢于提問并善于提問是探求知識的開始，也是創造性思維的起點。

總之，教師要實現有效提問，就要把握好提問的科學性、廣泛性、針對性、層次性和啟發性，運用有效的提問策略，做到明確提問目的，創設問題情境，認真準備問題，精心設計提問，把握好提問時機，運用好發問、候答、叫答、反饋、探問等策略，并及時引導學生進行反思，從而給學生充分的思維空間，激發學生的思維，促進學生思維的發展。

參考文獻：

1.程廣文.數學課堂提問研究——一種后現代視角．重慶：西南師范大學出版社，2006．

2.王惠萍，孫宏偉．兒童發展心理學．北京：科學出版社，2010．

3.王媛．小學數學教師“三階段”提問策略對課堂教學效果影響的研究．重慶：重慶師范大學，2020．