高中立體幾何中球體問(wèn)題的兩類(lèi)降維方法探究

吳婷

【摘要】高中立體幾何有著深厚的數(shù)學(xué)文化背景，與社會(huì)實(shí)踐息息相關(guān).而立體幾何中的球體是現(xiàn)實(shí)生活中最常見(jiàn)的數(shù)學(xué)模型之一.學(xué)生通過(guò)立體幾何球體部分知識(shí)的學(xué)習(xí)能更好地提升數(shù)學(xué)學(xué)科素養(yǎng)，以適應(yīng)今后的社會(huì)發(fā)展.然而，在實(shí)際教學(xué)過(guò)程中，不少學(xué)生表現(xiàn)出對(duì)球體問(wèn)題的畏難情緒，主要原因在于基礎(chǔ)知識(shí)概念的模糊、空間想象能力不足以及立體幾何到平面幾何的知識(shí)遷移能力不足等.基于此，文章從將球體問(wèn)題降維至球心所在平面，將球體問(wèn)題降維至其他輔助平面兩個(gè)方面指導(dǎo)學(xué)生使用“降維思想”，促使學(xué)生利用“降維思想”去解決球體問(wèn)題.學(xué)生掌握這兩種降維方法對(duì)于掌握立體幾何中的球體問(wèn)題有著重要意義.

【關(guān)鍵詞】立體幾何；球體；降維思想

引 言

降維思想泛指將一個(gè)復(fù)雜的數(shù)學(xué)問(wèn)題轉(zhuǎn)化為一個(gè)相對(duì)簡(jiǎn)單的問(wèn)題，從而達(dá)到簡(jiǎn)化解決數(shù)學(xué)問(wèn)題的思維模式.在處理與球相關(guān)的問(wèn)題時(shí)，教師可以指導(dǎo)學(xué)生進(jìn)行立體幾何和平面幾何知識(shí)間的遷移，實(shí)現(xiàn)數(shù)學(xué)上的降空間維度，從而將原本復(fù)雜的空間球體問(wèn)題轉(zhuǎn)化為更容易理解和求解的平面問(wèn)題.對(duì)于高中數(shù)學(xué)立體幾何球體問(wèn)題的降維策略，教師可嘗試指導(dǎo)學(xué)生進(jìn)行以下兩大類(lèi)降維處理方法.

一、將球體問(wèn)題降維至球心所在平面

過(guò)球心的平面截球產(chǎn)生的截面圓即“大圓”，大圓中涵蓋了球的關(guān)鍵要素，所以在進(jìn)行有關(guān)球的計(jì)算時(shí)，可以將空間問(wèn)題降維轉(zhuǎn)化至大圓所在平面，即運(yùn)用轉(zhuǎn)化化歸思想實(shí)現(xiàn)化球?yàn)閳A來(lái)解決問(wèn)題.在平面內(nèi)可以利用相似三角形關(guān)系、勾股定理、正余弦定理等幾何原理求解.

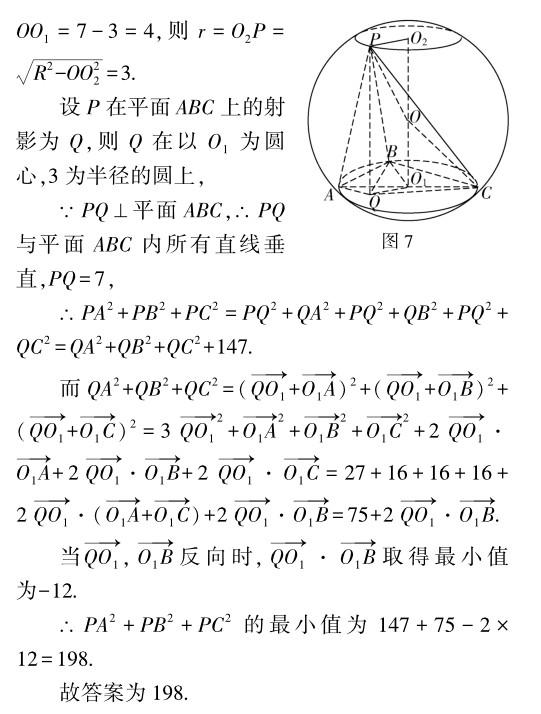
點(diǎn)評(píng) 該題通過(guò)投影技巧，將三棱錐中線段平方和問(wèn)題降維至外接球小圓內(nèi)的線段平方和問(wèn)題，結(jié)合向量方法優(yōu)化處理，亦可在該小圓所在平面建系實(shí)現(xiàn)幾何問(wèn)題代數(shù)化.

結(jié) 語(yǔ)

通過(guò)以上兩種降維策略，學(xué)生可以更深刻地理解“空間問(wèn)題平面化”的重要思想，在解決球體問(wèn)題時(shí)更好地理解和應(yīng)用相關(guān)的數(shù)學(xué)知識(shí).同時(shí)這兩種降維處理的方法可以幫助學(xué)生減少對(duì)空間概念的畏懼，更加直觀地理解和解決復(fù)雜的立體幾何問(wèn)題.因此，在教學(xué)中，教師可以通過(guò)實(shí)際案例和練習(xí)來(lái)引導(dǎo)學(xué)生善于利用動(dòng)態(tài)的思維，根據(jù)問(wèn)題中的關(guān)鍵信息進(jìn)行加工分析，提高他們解決立體幾何球體問(wèn)題的能力.任何一種思維形態(tài)的形成都是始于問(wèn)題，成于思考，用于實(shí)踐.教學(xué)中的灌溉滲透有利于學(xué)生邏輯思維和空間想象能力的發(fā)展，能更好地落實(shí)立德樹(shù)人的根本任務(wù).

【參考文獻(xiàn)】

[1]中國(guó)高考報(bào)告學(xué)術(shù)委員會(huì).高考試題分析（2023）[M].北京：現(xiàn)代教育出版社，2021.

[2]周明墩.談高中數(shù)學(xué)解題中的降維思維[J].中學(xué)數(shù)學(xué)，2021（19）：56-57.

[3]季峰.升維思考，降維解題：例談高考數(shù)學(xué)中的“高觀點(diǎn)”試題[J].中學(xué)數(shù)學(xué)，2021（3）：30-31，33.