一類涉圓錐曲線的兩條直線交點(diǎn)坐標(biāo)求解方法的研究

胡劍 李紅慶

【摘要】回眸2022年北京、浙江及全國甲、乙卷4套高考數(shù)學(xué)試題的壓軸題，研究者不難發(fā)現(xiàn)解析幾何是排在首位的，也的確壓準(zhǔn)了中學(xué)數(shù)學(xué)教學(xué)中的軸線，并且深深地切入考生的痛點(diǎn)———數(shù)學(xué)運(yùn)算策略、習(xí)慣與關(guān)鍵能力方法.通過縱向比較近5年高考解析幾何趨勢和橫向剖析2022年全國4套試題及北京、浙江等試題，研究者就會發(fā)現(xiàn)壓軸題其實(shí)都是涉圓錐曲線一條直線上點(diǎn)的坐標(biāo)表示另一點(diǎn)的坐標(biāo)的求解問題.順著命題發(fā)展延伸脈絡(luò)來觀察，涉圓錐曲線的兩條直線交點(diǎn)坐標(biāo)求解問題會成為新的熱點(diǎn).鑒于此，文章將就命題生成機(jī)理分析、命題生成案例舉隅、涉圓錐曲線兩條直線交點(diǎn)坐標(biāo)運(yùn)算問題進(jìn)行闡析.

【關(guān)鍵詞】涉圓錐曲線；直線交點(diǎn)；坐標(biāo)求解；關(guān)鍵能力；蝴蝶定理

引 言

通過縱向分析近5年高考解析幾何命題趨勢的走向，橫向研究2022年高考試題中解析幾何命題的共性，研究者發(fā)現(xiàn)2022年解析幾何命題都是一類涉圓錐曲線一條直線上點(diǎn)的坐標(biāo)表示另一點(diǎn)的坐標(biāo)的求解問題.順著解析幾何命題發(fā)展趨勢脈絡(luò)來觀察，涉圓錐曲線的兩條直線交點(diǎn)坐標(biāo)求解問題會成為新的熱點(diǎn)，其本質(zhì)是阿氏圓的相關(guān)元和蝴蝶定理的導(dǎo)向.

一、命題生成機(jī)理分析

這類問題是兩條直線中每條直線中的線段都只有一個(gè)端點(diǎn)在圓錐曲線上，命題涉及的條件與結(jié)論都可能隱含著圓錐曲線某個(gè)重要的性質(zhì)，多數(shù)都涉及阿波羅尼斯（Apollonius）圓（以下簡稱阿氏圓）的相關(guān)元的關(guān)系，蝴蝶定理和圓錐曲線的通性問題，先從高中數(shù)學(xué)需求方面簡單地介紹阿氏圓.

（一）阿波羅尼斯（Apollonius）圓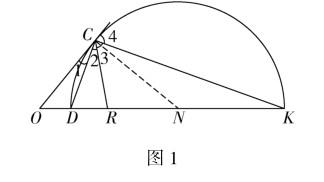

平面內(nèi)動點(diǎn)C到兩定點(diǎn)O，R的距離之比是不等于1的常數(shù)，那么動點(diǎn)C的軌跡就稱為阿氏圓（如圖1），其中阿氏圓N在直線OR上直徑端點(diǎn)為D，K，并且點(diǎn)C是直線OC與阿氏圓N的切點(diǎn)，射線CD是∠OCR的平分線（∠1=∠2），射線CK是△OCR的外角平分線（∠3=∠4），由圓的切割線定理，得到重要結(jié)論OC2=OD·OK，這個(gè)結(jié)論往往體現(xiàn)在命題的結(jié)論中.

（二）阿波羅尼斯（Apollonius）圓的相關(guān)元

文[1]中曾介紹過蝴蝶定理在圓錐曲線與直線位置關(guān)系中的應(yīng)用，其實(shí)它也是阿氏圓的性質(zhì)的具體體現(xiàn)，現(xiàn)在介紹它的其他應(yīng)用，并把這些性質(zhì)統(tǒng)稱阿氏圓的相關(guān)元的性質(zhì).

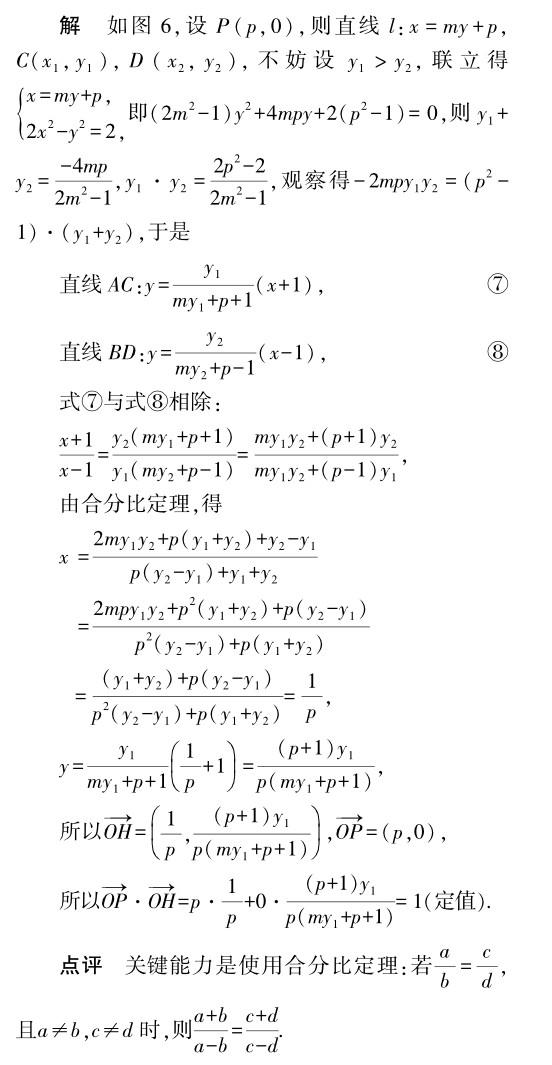
結(jié) 語

文章借助解決涉圓錐曲線的兩條直線交點(diǎn)的問題，明確學(xué)生的關(guān)鍵能力是數(shù)學(xué)運(yùn)算及利用同構(gòu)式進(jìn)行化簡，從而靈活應(yīng)用廣義一元一次方程的多解條件解決定值、定點(diǎn)、定線問題.

【參考文獻(xiàn)】

[1]駱銀海，李紅慶.解析幾何中一類需要優(yōu)先考慮用字母運(yùn)算的問題及其解法[J].數(shù)學(xué)通訊，2023（1）：32-34，37.

[2]李紅慶.跟我學(xué)解高中數(shù)學(xué)題（第2版）[M].哈爾濱：哈爾濱工業(yè)大學(xué)出版社，2021.

[3]李紅慶.高考數(shù)學(xué)圈題典釋（第2版）[M].北京：清華大學(xué)出版社，2013.