基于氣象觀測數據建立卷積神經網絡算法反演PM2.5

王雨軒 周甘凝 許文龍 秦孟晟

收稿日期：2023-11-10

基金項目：江蘇省青年基金項目（KQ202330）。

作者簡介：王雨軒（1993—），男，揚州寶應人，助理工程師，主要從事氣溶膠、大氣探測研究。

摘 要：利用揚州市氣象觀測站點和中國環境監測總站的逐小時數據估算PM2.5的各相關組合因子，然后利用CNN卷積神經網絡算法構建反演PM2.5質量濃度的機器學習模型。結果表明：（1）利用 CNN卷積神經網絡算法反演PM2.5是有效且可行的，且比一般的線性回歸算法效果更佳，為反演PM2.5提供了一種新的機器學習方法。（2）在影響PM2.5反演的各輸入變量因子中，PM10與能見度變量為高相關因子。利用神經卷積網絡算法反演PM2.5理論上反演精度能夠隨著輸入信息增多而不斷提高。

關鍵詞：CNN卷積神經網絡算法；氣象觀測數據；PM2.5

中圖分類號：P407.7 文獻標識碼：B文章編號：2095–3305（2024）03–0-03

PM2.5是指懸浮在空中的空氣動力學當量直徑≤2.5 μm的細顆粒物，其嚴重影響環境、氣候，危害人體健康，破壞生態系統[1]。在排放源相對穩定的情況下，氣象因素也是污染物形成、傳輸及沉降等環節的重要原因[2-3]。因此，從氣象學的角度分析大氣污染的規律和機制，有助于為大氣污染防治提供科學支撐。盡管環境監測站點對近地面PM2.5直接測量的精度較高，但在監測點的數量和分布上的局限性較大，只能反映監測站點小范圍內PM2.5的變化。因此，有必要利用氣象觀測數據對PM2.5乃至其他一些常見的大氣污染物進行模擬反演，繼而能大范圍地揭示常見大氣污染物的時空變化規律。

氣象要素對PM2.5的形成起著促進或改善作用[4]。魏文靜等[5]對山東省17個地市的研究表明，PM2.5受氣溫和降水的影響較為顯著；黃小剛等[6]研究表明，氣象對PM2.5污染有一定調節作用，PM2.5與氣溫、風速、濕度和降水量呈線性遞增或遞減關系。

前人針對PM2.5也開展了多途徑的反演，一般較常用的方法是多元線性回歸法。相關學者利用多元線性回歸模型分析2014年APEC和2015年國慶閱兵期間氣象要素對PM2.5的影響；何鈺清等[7]利用多元線性回歸分析法建立了PM2.5月均濃度的預測模型。但顆粒物濃度的變化與氣象條件之間呈現很強的非線性關系，因此，傳統的多元線性回歸模型預測PM2.5質量濃度的局限性較大[8]。

近年來，隨著機器學習技術的發展，已有不少學者利用神經網絡算法來估算PM2.5。陳兵紅等[9]應用多元線性回歸和隨機森林方法反演浙江省PM2.5濃度；石靈芝等[10]運用BP人工神經網絡預測短期的PM10小時數據；胡娟等[11]嘗試從遙感的角度利用BP神經網絡算法反演PM2.5；還有學者基于隨機森林算法的氣象歸一化方法評估了全球11個城市2020年初的PM2.5、O3等濃度的變化情況。機器學習基于統計學原理，理論上只要輸入的信息越多越詳細，神經算法的效果就越好。不同于以往傳統的對復雜的大氣污染的物理化學過程和衛星遙感原理的研究，神經網絡算法為PM2.5的反演提供了新途徑。

1 數據來源及算法原理

1.1 數據來源

聚焦揚州地區，大氣污染數據來源于中國環境監測總站，包括PM2.5和PM10，使用其逐小時數據計算日平均值。相應的氣象數據來源于揚州市氣象局自動觀測站監測數據。時間段為2018年1月1日—2022年11月30日。其中，2020年2月1日—6月30日數據缺失，不在研究范圍內。

1.2 算法原理

1.2.1 卷積神經網絡算法

卷積神經網絡（Convolution Neural Networks，CNN）

最早由Yann LeCun等提出。CNN 卷積神經網絡是一種包含卷積計算且有深度結構的前饋神經網絡，是深度學習算法代表之一[12]。近年來，隨著機器學習方法的不斷發展，CNN卷積神經網絡算法也逐漸被應用于大氣科學領域。 典型的CNN網絡結構主要包含輸入層、隱含層和輸出層（圖1）。其中，隱含層主要包含卷積層、池化層和全連接層。數據通過輸入層后，依次在各個神經網絡層傳遞，每一網絡層都能夠獲取對平移、縮放和旋轉不變的觀測數據的顯著特征。隱含層的主要作用是實現特征提取。

1.2.2 多元線性回歸

多元線性回歸模型（MLR）是應用較為廣泛的統計方法，可用于研究因變量與多個自變量之間的關系。建立多元線性回歸模型可較好地解釋以及估計因變量的值，其一般形式為：

Y=β0＋β1x1＋β2x2＋…＋βmxm＋ε（1）

式（1）中，Y為因變量，x1，x2，…，xm為自變量，β0，

β1，…，βm為回歸系數，ε為隨機誤差。

1.2.3 模型變量選擇及評價指標

嘗試建立基于氣象觀測數據的卷積神經網絡算法（CNN）反演PM2.5的模型，輸入氣象觀測數據，隨機挑選輸入的日數據的70%作為神經網絡訓練集，30%作為結果對比集。反演精度評價指標包括：

均方根誤差（Root Mean Squared Error，RMSE）。

RMSE=（2）

均方絕對百分比誤差（Mean Absolute Percentage Error，MAPE）。

MAPE=||（3）

決定系數（Coefficient of Determination，R2）。

（4）

（5）

式（2）～式（5）中，為PM2.5實測值，為多元線性回歸MLR或卷積神經網絡CNN反演得到的PM2.5。

2 結果與分析

2.1 PM2.5反演模型的建立

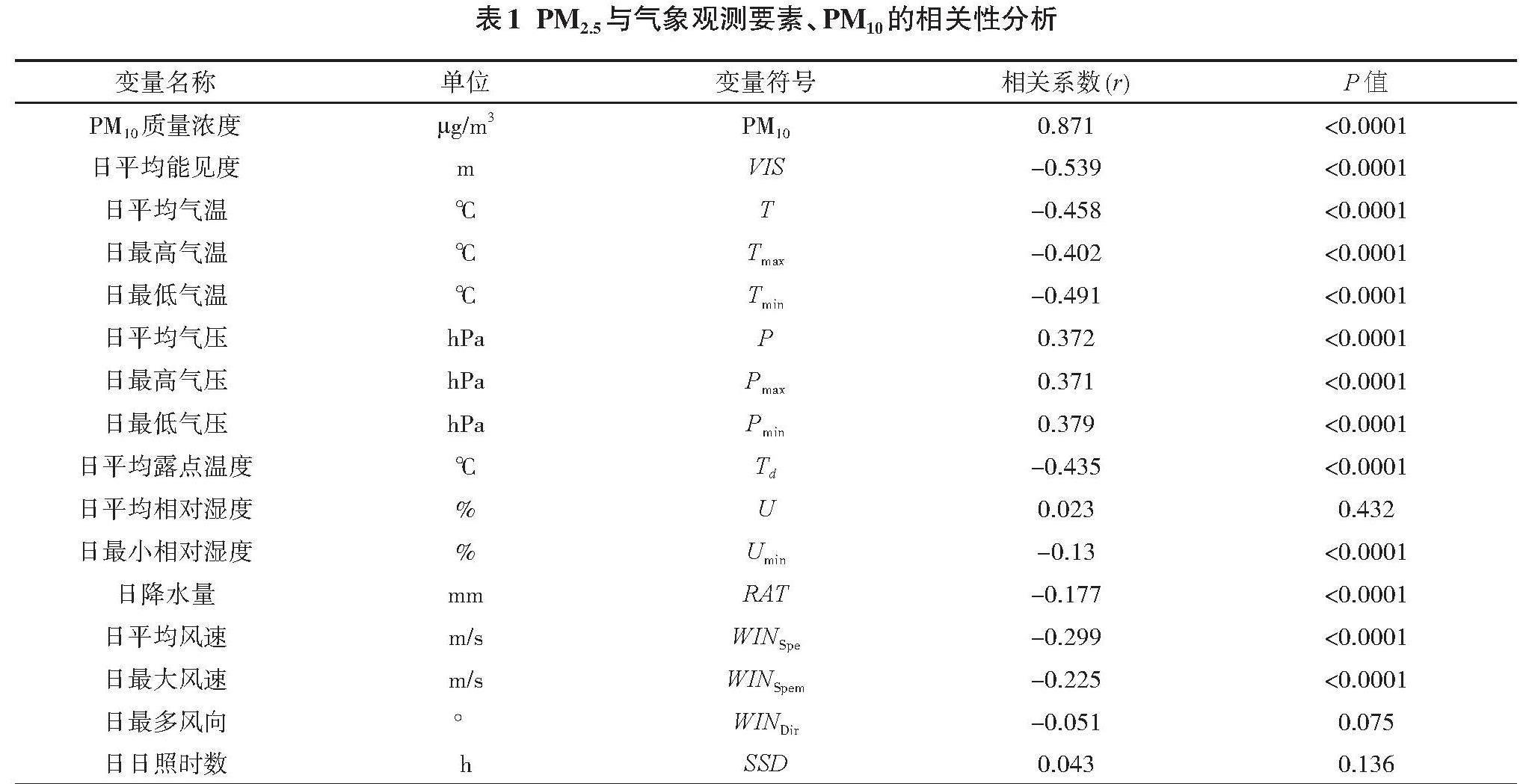
輸入參數包括PM10、能見度、溫度系列參數、氣壓系列參數、相對濕度系列參數，露點溫度、風向風速系列參數、降水量和日照時數（表1）。利用皮爾遜相關系數r估計變量x，y間的相關性。r值介于[-1，1]，r>0表示正相關，即兩變量同向相關，反之表示兩變量異向相關。r絕對值越接近1，表示兩變量的關系越密切；越接近0，表示兩變量的關系越不密切。表1是各變量因子與PM2.5的相關系數r和顯著性水平P。該表可以反映出，與PM2.5相關性較大的變量為PM10、VIS。其中，PM10、P、Pmax、Pmin、U、SSD這6個變量與PM2.5呈正相關關系，剩下的10個變量與PM2.5呈負相關關系。還可以發現，除了U、WINDir和SSD，其余變量均在0.01水平（雙側）上相關性顯著。

2.2 CNN與MLR反演性能對比

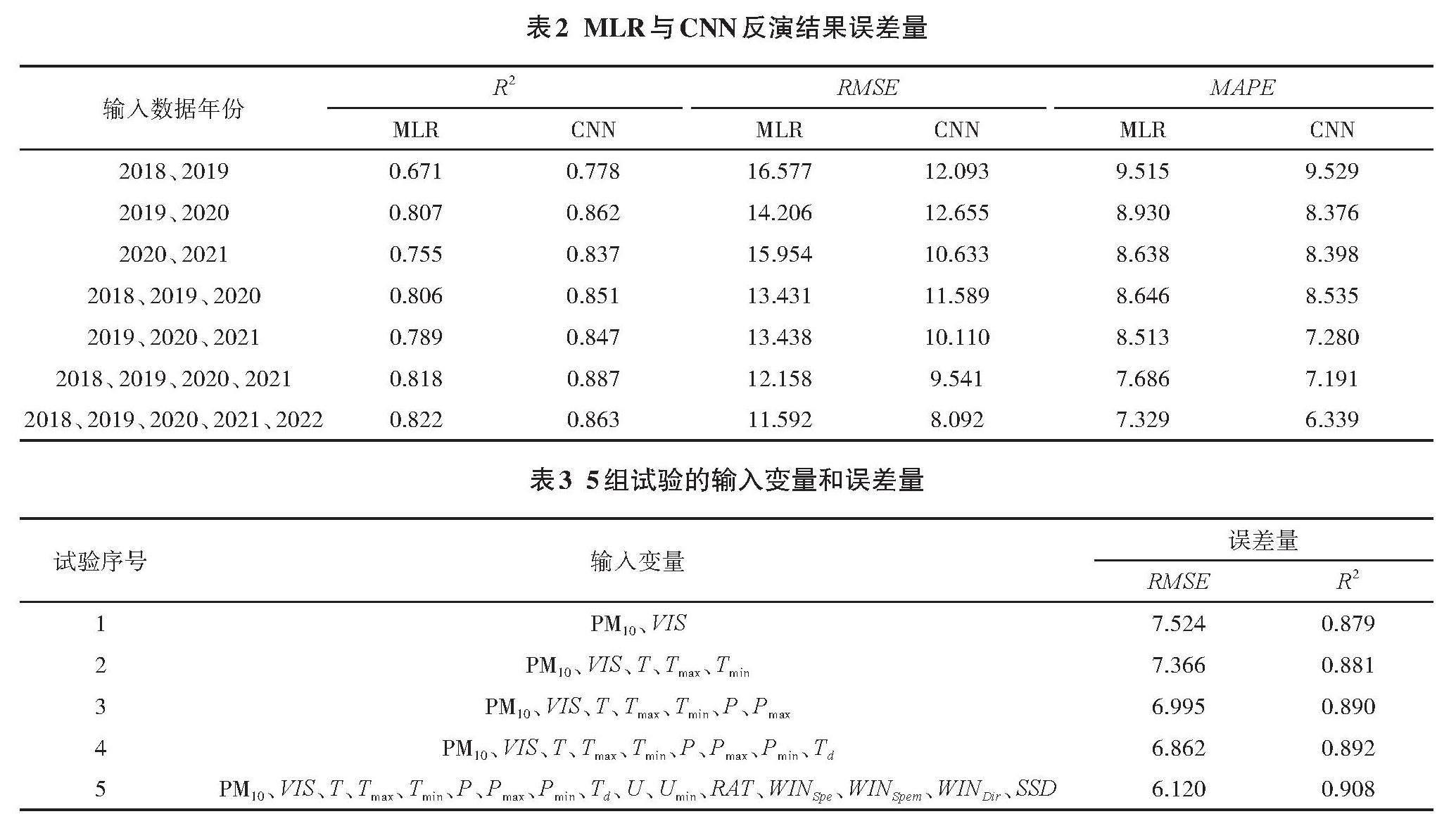
基于上述建立的PM2.5反演模型，輸入變量首先采用“試驗5”的變量組合（表3），CNN和MLR的反演結果對比見表2。其中，按輸入數據的年份分為2年期、3年期、4年期和5年期。首先可以整體性地看出，MLR的R2值均小于CNN的R2值，MLR的RMSE和MAPE均大

于CNN的RMSE和MAPE，說明CNN的反演精度要優于MLR。然后對2年期的3組數據和3年期的2組數據取平均。

2年期的3組數據平均值為：

MLR：R2=0.744，RMSE=15.579，MAPE=9.028；

CNN：R2=0.826，RMSE=11.794，MAPE=8.768。

3年期的2組數據平均值為：

MLR：R2=0.798，RMSE=13.435，MAPE=8.580；

CNN：R2=0.849，RMSE=10.850，MAPE=7.908。

由此可以看出，隨著輸入數據年份數的增加，CNN

和MLR的反演性能指標都在提升，其中，R2值隨著年份數的增加而增大，RMSE和MAPE隨著年份數的增加而減小。表明反演的相關性不斷提升，誤差不斷減小，精度有所提高。因此，若能有長時間的年份數據作為神經網絡的訓練集，反演的PM2.5理論上十分接近實際的PM2.5。

2.3 CNN模型輸入參數的分析

在驗證CNN模型的反演精度后，有必要對CNN模型的輸入參數做研究，探討各輸入參數對反演精度的影響情況。考慮依次增加輸入參數，即“試驗1”至“試驗5”（表3）。由于PM10和能見度VIS與PM2.5的相關性較大，因此，將其作為基本的輸入參數，即“試驗1”，后依次增加溫度系列參數、氣壓系列參數、露點溫度，即“試驗2”至“試驗4”，“試驗5”包含研究全部的氣象觀測數據參數。從反演的誤差結果可以看出，隨著輸入參數的不斷增加，RMSE值不斷減小，R2值不斷增加，說明反演精度不斷提高，這也與上述介紹的機器學習的特性相對應：理論上，輸入的信息越多，機器學習的效果越好。

3 結論

（1）利用 CNN卷積神經網絡算法反演PM2.5是有效可行的，且比一般的線性回歸算法效果更好，為反演PM2.5提供了一種新的機器學習方法。

（2）在影響PM2.5反演的各輸入變量因子中，PM10與能見度變量為高相關因子。利用神經卷積網絡算法反演PM2.5理論上反演精度能夠隨著輸入信息增多而不斷提高，具體有待進一步研究。

參考文獻

[1] 郭新彪，魏紅英.大氣PM2.5對健康影響的研究進展[J].科學通報，2013，58（13）：1171-1177.

[2] 余鐘奇，馬井會，毛卓成，等.2017年上海臭氧污染氣象條件分析及臭氧污染天氣分型研究[J].氣象與環境學報， 2019，35（6）：46-54.

[3] 嚴文蓮，劉端陽，康志明，等.江蘇臭氧污染特征及其與氣象因子的關系[J].氣象科學，2019，39（4）：477-487.

[4] 馮萬富，沈新志，周繼良，等.基于氣象要素的雞公山景區PM10濃度預測[J].河南大學學報（自然科學版），2022，52（5）： 571-578.

[5] 魏文靜，謝炳庚，周楷淳，等.2013—2018年山東省大氣PM2.5和PM10污染時空變化及其影響因素[J].環境工程， 2020，38（12）：103-111.

[6] 黃小剛，趙景波，孫從建，等.汾渭平原PM2.5空間分布的地形效應[J].環境科學，2021，42（10）：4582-4592.

[7] 何鈺清，李磊，楊紅龍，等.深圳PM2.5濃度變化趨勢及其月尺度預測方法[J].科學技術與工程，2022，22（1）：400-408.

[8] 刁一偉，王紅磊，沈利娟，等.2015—2021年南京市大氣污染特征及污染個例研究[J].環境科學研究，2023，36（2）：260-272.

[9] 陳兵紅，靳全鋒，柴紅玲，等.浙江省大氣PM2.5時空分布及相關因子分析[J].環境科學學報，2021，41（3）：817-829.

[10] 石靈芝，鄧啟紅，路嬋，等.基于BP人工神經網絡的大氣顆粒物PM10質量濃度預測[J].中南大學學報（自然科學版），2012，43（5）：1969-1974.

[11] 胡娟，鄭軍，許文龍，等.利用多源數據建立GA-BP算法模型估算PM2.5的研究[J].氣象科學，2021，41（3）：314-322.

[12] 姚姝含，官莉.基于星載紅外高光譜觀測用機器學習算法反演大氣溫濕廓線[J].紅外與激光工程，2022，51（8）：461-472.