核心素養視角下高中數學教材習題與課程標準的一致性研究

［摘 要］ 基于SEC模型，并結合數學學科核心素養相關理論框架，從內容主題和認知水平兩個維度對人教A版教材和北師大版教材高中數學教材中的三角函數習題與《普通高中數學課程標準（2017年版2020年修訂）（簡稱課程標準）》進行一致性研究. 研究發現，北師大版教材與課程標準的一致性更高.

［關鍵詞］ 核心素養；一致性研究；教材習題；課程標準

提出問題

《普通高中數學課程標準（2017年版2020年修訂）》（簡稱課程標準）正式提出數學學科核心素養，并將其描述為學生通過數學學習而逐步形成的正確價值觀、必備品格和關鍵能力，具體包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析［1］.

課程標準是教材編寫、教學、評估和考試命題的依據，是國家管理和評價課程的基礎［2］. 教材作為課程內容的重要載體，其編寫需要與課程標準保持一致. 習題作為教材內容的重要組成部分，是教學過程中不可或缺的因素. 一方面，習題是幫助學生掌握知識、提升能力的重要工具；另一方面，習題是教師了解學生的知識掌握情況的重要途徑. 余元慶認為習題配備得好不好，直接影響學生的學習質量的高低［3］. 雖然學界對試卷與課程標準有大量的一致性研究［4-7］，但有關教材習題與課程標準的一致性研究較少. 有學者發現，在數學教學實踐中，不少教師沒有充分挖掘教材中習題的功能，盲目使用教輔［8］. 三角函數是一類最典型的周期函數，提供了對周期性變化的思考，在高中數學教材中占有重要地位［9］.

通過上述多方面的思考，本研究以核心素養為出發點，對現行教材中的三角函數習題與課程標準進行了一致性比較，希望從中發現問題，以便為后續改進提供參考和借鑒.

研究設計

1. 研究對象

鑒于人民教育出版社和北京師范大學出版社2019年出版的普通高中數學教科書（分別簡稱人教A版教材和北師大版教材）使用范圍較廣且影響較大，本研究選定這兩版教材中的三角函數習題與課程標準進行一致性比較，涉及教材中的“例題”“練習題”“習題”“復習參考題”等版塊.

2. 研究工具

John Smithson和Andrew Porter等人在Norman L.Webb的研究基礎上開發了SEC一致性分析模型，通常用于判斷教學項目與課程標準之間的一致性［10］.

本研究采用SEC模型從內容主題和認知水平兩個維度來探討教材習題和課程標準的一致性程度. 研究過程大致分為三步：

第一，建立“5×3”的二維矩陣. 在內容主題維度上，參照課程標準，將“三角函數”章節劃分為“角與弧度”“三角函數的概念與性質”“同角三角函數的基本關系式”“三角恒等變換”和“三角函數的應用”五部分. 在認知水平維度上，根據喻平教授所提的數學核心素養評價框架，劃分為知識理解、知識遷移、知識創新三類［11］. 知識理解表現為初步了解、初步體會、感受、認識知識；知識遷移表現為掌握、利用知識，運用多種知識解決復雜問題；知識創新表現為設計不同方法，選擇不同知識解決非常規問題［11］.

第二，將二維數據轉化為比率分別填入三張二維矩陣表.

第三，利用Porter一致性公式［12］P=1-算出結果. 其中n是二維框架單元格的總數，a表示課程標準矩陣的第i個單元格所對應的數值，b表示教材矩陣的第i個單元格所對應的數值；P為一致性系數，范圍在0到1之間，越趨近于1代表一致性越高.

3. 編碼方法

分析教材和課程標準時，首先，將三角函數的五個內容主題“角與弧度”“三角函數的概念與性質”“同角三角函數的基本關系式”“三角恒等變換”和“三角函數的應用”分別編碼為1，2，3，4，5；其次，將數學抽象、邏輯推理、數學建模、數學運算和直觀想象分別編碼為A，R，M，O，I（由于“三角函數”章節基本不涉及數據分析素養，所以將其去除）；再者，將知識理解、知識遷移和知識創新分別編碼為L1，L2，L3. 在認知水平分布時，可簡寫為1，2，3，例如A1表示數學抽象知識理解水平.

需要特別說明的是，分析教材時，若一道題有多個小問，則將每一小問記為一道習題，根據已有研究［13］，若一道習題涉及多個核心素養，則編碼時只選取其中最主要的兩個核心素養.

編碼結果

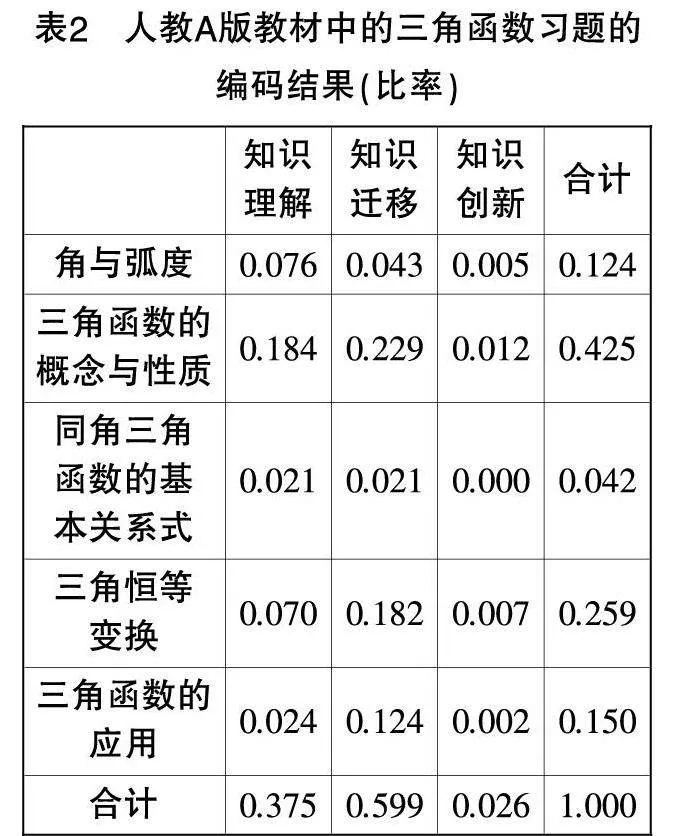
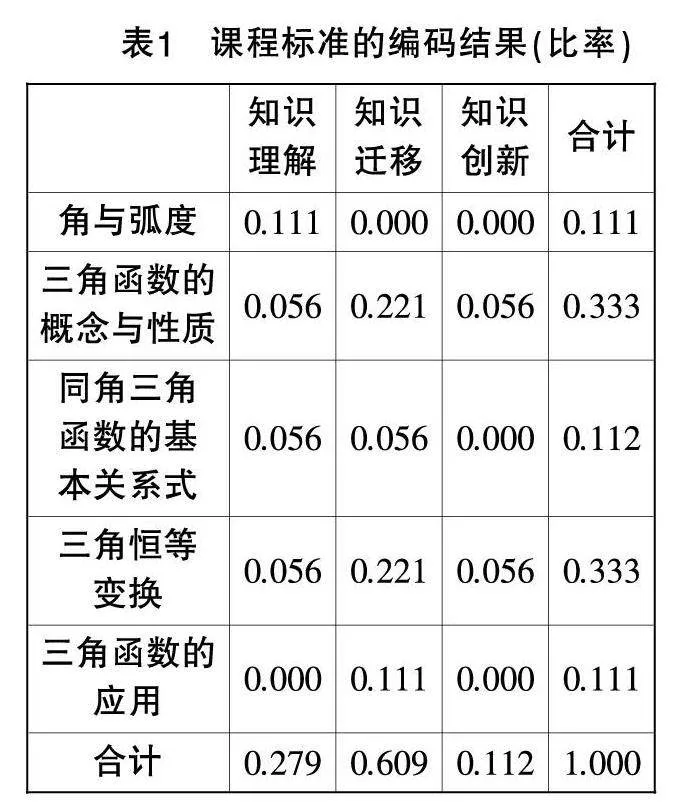
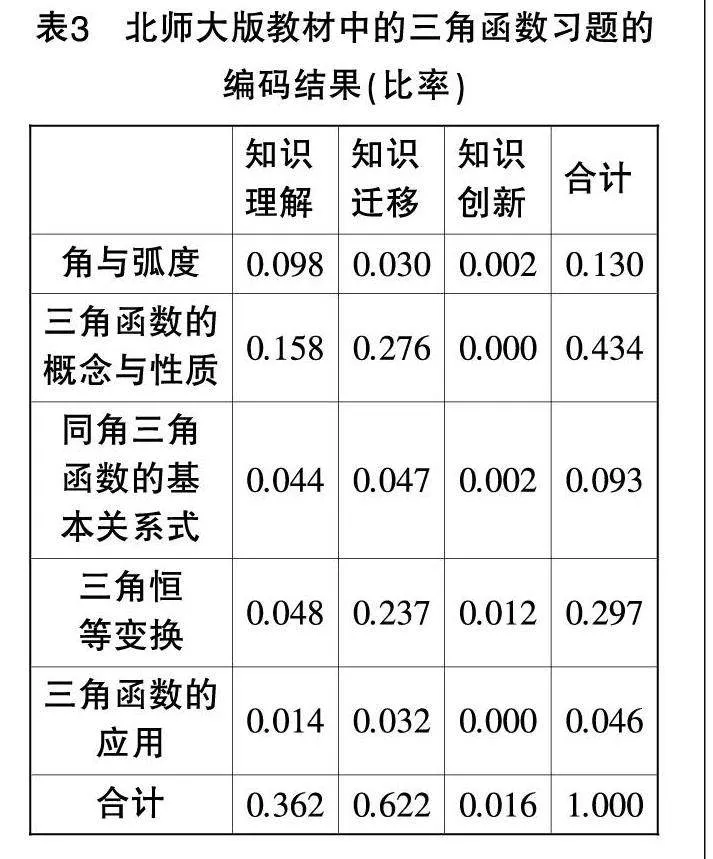
為了減少人工編碼的誤差，編碼工作由兩位研究人員獨立完成，然后用SPSS26.0軟件對編碼結果進行Kappa一致性檢驗，得出Kappa值為0.867，說明編碼結果具有良好的一致性，對分歧點進行討論修改，形成最終一致的編碼結果，數據結果見表1至表3.

結果與分析

1. 兩版教材中的三角函數習題與課程標準的一致性系數

根據Porter一致性公式，計算人教A版教材和北師大版教材中的三角函數習題與課程標準的P值分別為0.7641，0.7807.Gavin W.Fulmer利用R軟件通過隨機模擬，得出“5×3”編碼標準（30標準點）臨界值范圍為0.8667～0.9444［14］. 雖然北師大版教材與課程標準的一致性系數略高于人教A版教材與課程標準的一致性系數，但二者均低于臨界值下限0.8667，說明兩版教材中的三角函數習題與課程標準的一致性程度較弱.

2. 內容主題維度

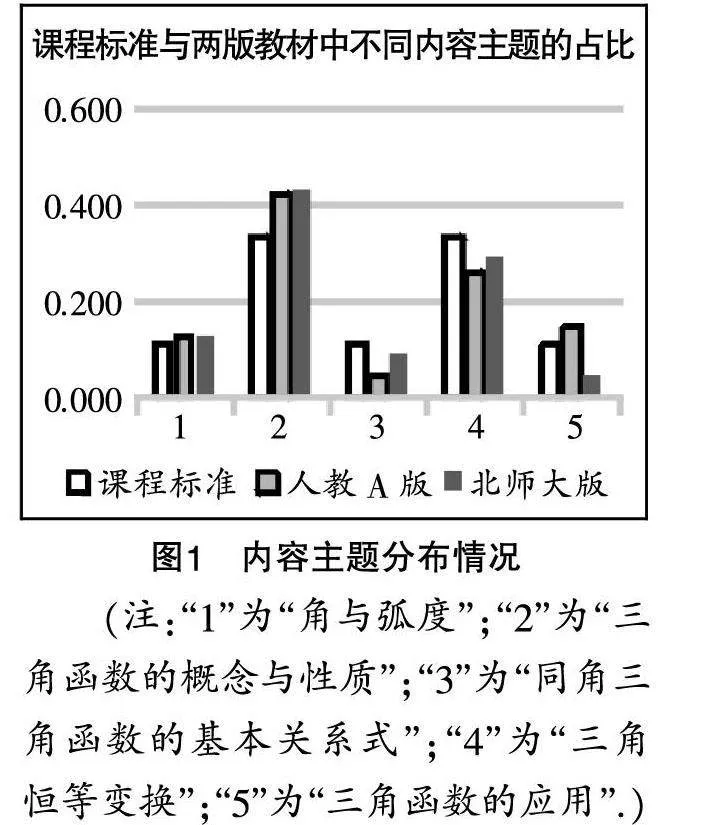
（1）內容主題維度下的兩版教材與課程標準之間的差異

由圖1可知，總體上課程標準中內容主題的占比為：三角函數的概念與性質=三角恒等變換>角與弧度=同角三角函數的基本關系式=三角函數的應用. 兩版教材與課程標準差別不大. 其中，“三角函數的概念與性質”和“三角恒等變換”的占比均超過均值0.2，而“角與弧度”“同角三角函數的基本關系式”和“三角函數的應用”的占比則均在均值0.2之下.

從內容主題來看，對于“三角函數的概念與性質”和“角與弧度”，在兩版教材中的占比都高于課程標準，其中人教A版教材更接近課程標準；對于“同角三角函數的基本關系式”和“三角恒等變換”，在兩版教材中的占比都低于課程標準，其中北師大版教材更接近課程標準；對于“三角函數的應用”，在人教A版教材中的考察比重高于課程標準，而北師大版教材的考察比重則低于課程標準.

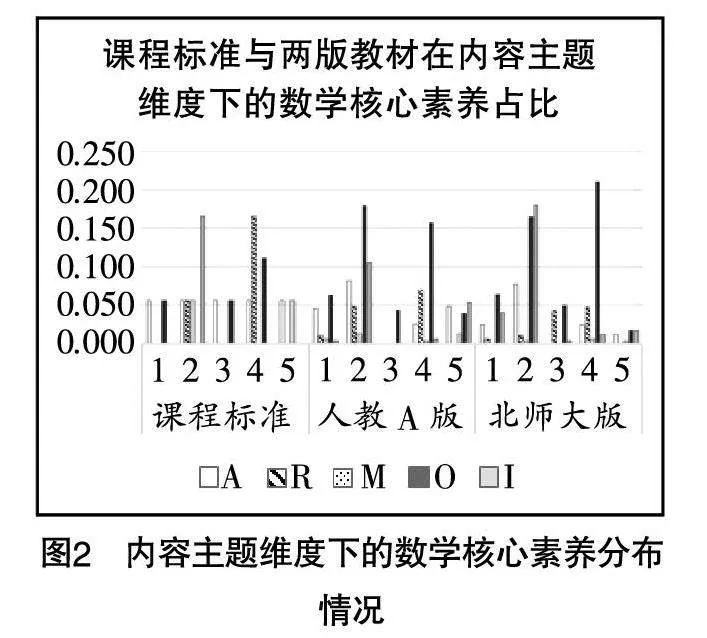
（2）內容主題維度下的數學核心素養分布情況

根據統計后的編碼結果得到課程標準、人教A版教材和北師大版教材在內容主題維度下的數學核心素養的分布情況，如圖2所示.

由圖2可知，在“角與弧度”的維度下，課程標準側重于培養數學運算和數學抽象；人教A版教材同樣如此，但考查數學抽象的比重略小于課程標準，考查數學運算的比重略大于課程標準；相較于課程標準，北師大版教材側重于培養數學運算的同時，考查直觀想象的比重大于數學抽象.在“三角函數的概念與性質”的維度下，課程標準側重于培養直觀想象，同時注重對數學建模、邏輯推理和數學抽象的培養，并未涉及數學運算；而人教A版教材對數學運算的考查比重最大，其次為直觀想象，考查數學建模的比重最小，且明顯小于課程標準；北師大版教材考查比重最大的核心素養與課程標準相同，均為直觀想象，其次為數學運算，數學建模最小，其中直觀想象、數學建模的比重明顯小于課程標準. 在“同角三角函數的基本關系式”的維度下，課程標準側重于數學運算和數學抽象的培養；人教A版教材只涉及數學運算的考查；北師大版教材側重于數學運算和邏輯推理的培養. 在“三角恒等變換”的維度下，課程標準側重于邏輯推理、數學運算和數學抽象的培養；人教A版教材考查數學運算的比重高于課程標準，考查邏輯推理和數學抽象的比重均低于課程標準，此外，人教A版教材還有較少的關于數學建模和直觀想象的考查；北師大版教材考查數學運算的比重明顯高于課程標準，考查邏輯推理和數學抽象的比重則均低于課程標準，此外，北師大版教材還考查了直觀想象和數學建模. 在“三角函數的應用”的維度下，課程標準側重于數學建模和數學抽象的培養；人教A版教材在這兩項上的考查比重均低于課程標準，另外考查了數學運算和直觀想象；北師大版教材對該主題的考查比重較低，且對數學建模和數學抽象的考查比重均低于課程標準.

3. 認知水平維度

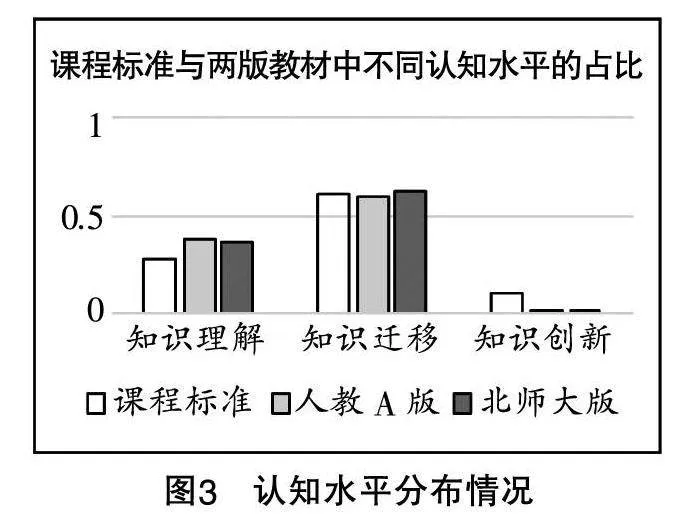
（1）認知水平維度下的兩版教材與課程標準之間的差異

由圖3可知，對于認知水平的分布，課程標準主要集中在知識遷移，其次是知識理解，最后是知識創新，兩版教材也有同樣的趨勢.對于知識遷移水平，在人教A版教材中的占比低于課程標準，而在北師大版教材中的占比則高于課程標準；對于知識理解水平，在兩版教材中的占比均高于課程標準；對于知識創新水平，在兩版教材中的占比均遠低于課程標準.

（2）認知水平維度下的數學核心素養分布情況

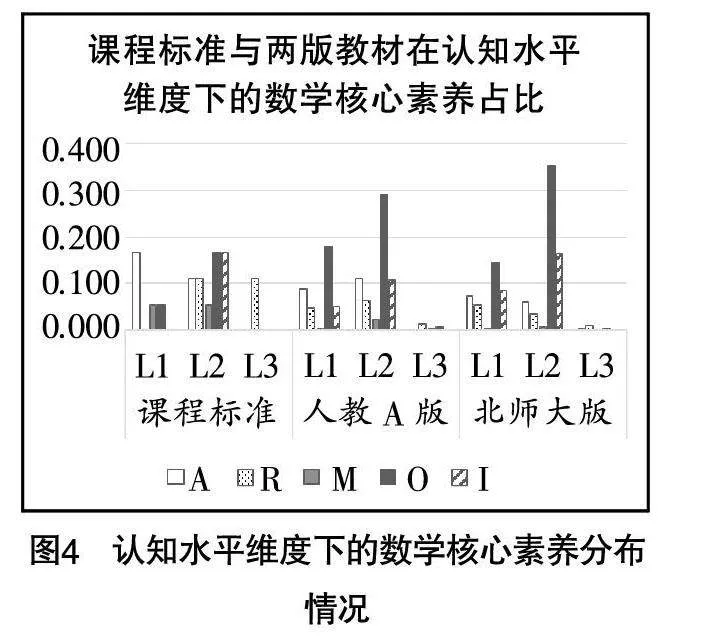
根據統計后的編碼結果得到課程標準、人教A版教材和北師大版教材在認知水平維度下的數學核心素養分布情況，如圖4所示.

由圖4可知，參照課程標準，在認知水平上，兩版教材習題的數學核心素養的分布很不均衡.在知識理解上，在課程標準中，數學抽象的占比最多，其次為數學運算和數學建模；在人教A版教材中，數學運算的占比最大，其次為數學抽象，數學建模的占比最小，數學運算的占比大于課程標準，數學抽象和數學建模的占比均小于課程標準；在北師大版教材中，占比最大的依然是數學運算，大于課程標準，數學抽象和數學建模的占比均小于課程標準.在知識遷移上，課程標準對五項核心素養均有所考查，占比最大的是直觀想象和數學運算；在人教A版教材中，占比最大的是數學運算，而且明顯大于課程標準，但邏輯推理、數學建模和直觀想象的占比均小于課程標準；在北師大版教材中，數學運算的占比最大，超過了課程標準兩倍. 在知識創新上，課程標準只涉及邏輯推理，兩版教材均涉及邏輯推理，且占比均小于課程標準.此外，人教A版教材還涉及數學運算、數學建模和直觀想象，北師大版教材涉及數學抽象和數學運算.

結論與建議

通過對課程標準與兩版教材的一致性比較，得到如下結論：

根據Porter一致性公式可得，人教A版教材和北師大版教材中的三角函數習題與課程標準的一致性系數均低于臨界值下限，兩版教材中的三角函數習題與課程標準的一致性不強，北師大版教材比人教A版教材更接近臨界值下限.

在內容主題上，人教A版教材與北師大版教材的內容占比與課程標準相差不大，差距基本上都不超過0.1. 兩版教材在不同內容主題上的數學核心素養的考查有所不同，在“角與弧度”“同角三角函數的基本關系式”和“三角恒等變換”三個內容主題上，人教A版教材習題對數學核心素養的考查，相較于北師大版教材，更符合課程標準的核心素養要求；在“三角函數的概念與性質”和“三角函數的應用”兩個內容主題上，北師大版教材習題對數學核心素養的考查，相較于人教A版教材，更符合課程標準的核心素養要求.

在認知水平上，以課程標準作為參照，兩版教材在認識水平維度下的核心素養占比不同. 整體上，課程標準和兩版教材對認知水平的考查均是“知識遷移>知識理解>知識創新”，這與課程標準是相吻合的.在知識理解上，課程標準中數學抽象的占比最大，而北師大版教材和人教A版教材是數學運算占比最大. 在知識遷移上，兩版教材中數學運算的占比都遠超課程標準，但對于直觀想象的重視程度存在不足；在知識創新上，課程標準只考查邏輯推理，兩版教材對五項核心素養均有考查，北師大版教材對核心素養的考查與課程標準的要求更加一致.

課程標準對核心素養的考查比例適中，但兩版教材對三角函數習題的編制都傾向于培養學生的數學運算核心素養，這可能導致學生發展失衡. 在今后教材修訂與完善的過程中，可從以下幾方面去考慮.

《普通高中數學課程標準（2017年版）》首次提出六大數學核心素養，它們既相互獨立，又彼此交融，是一個有機整體. 以課程標準作為參照，人教A版教材和北師大版教材中的三角函數習題對核心素養的考查分布并不均衡，兩版教材習題尤其注重培養數學運算，這與課程標準的要求并不一致. 教材代表編寫者對課程標準的一種理解，卻未必真正代表課程標準的本來含義［15］. 因此，在教材編寫過程中，教材習題編寫者應仔細研讀課程標準，圍繞課程標準要求，合理設置對數學核心素養的考查比例，培養和提升學生的數學核心素養. 兩版教材中的三角函數習題對數學建模素養和直觀想象素養的考查較少，而數學建模素養和直觀想象素養都是培養學生數學能力的重要素養，因此建議教材增加培養數學建模和直觀想象素養的習題.

長期以來，我國中學生的數學水平在國際上遙遙領先，與多年來我國重視“雙基”密不可分. 但在知識創新水平上，兩版教材的權重都低于課程標準. 因此，教材應增加一些創新性、開放性習題，引導學生多角度分析問題、解決問題，增強學生的創新意識. 例如北師大版教材第八節中的“水車問題”，要求學生利用所學的三角函數知識建立水車運動模型，并且考慮當河水上漲或旱季河流量減少對數學模型的影響. 這種富有濃厚生活氣息，具有開放性、發展性與實踐性的習題，結合閱讀、寫作、建模等實踐活動，可為學生的發展搭建平臺.

參考文獻：

［1］ 中華人民共和國教育部. 基礎教育課程改革綱要（試行）［S］. 北京：人民教育出版社，2001.

［2］ 中華人民共和國教育部. 普通高中數學課程標準（2017年版2020年修訂）［S］. 北京：人民教育出版社，2020.

［3］ 余元慶. 談談習題的配備與處理——介紹幾本外國中學數學課本中的習題配備［J］. 數學通報，1980（03）：6-10.

［4］ 繆琳，陳清華，蘇圣奎. 義務教育課程標準與中考試卷一致性分析——以2013—2016年廈門市中考數學試卷為例［J］. 數學教育學報，2017，26（05）：44-48.

［5］ 徐帆，張勝元，孫慶括. 初中數學學業評價與課程標準的一致性研究——以福建省五套中考數學試卷為例［J］. 數學教育學報，2019，28（03）：98-102.

［6］ 張定強，裴陽. 新高考改革背景下數學試卷與課標一致性研究——以2017—2018年全國Ⅱ卷與浙江卷為例［J］. 數學教育學報，2019，28（04）：55-60.

［7］ 武麗莎，朱立明，王久成. 數學學科核心素養高考測評與課程標準一致性研究——以2019—2021年高考數學Ⅰ試卷為例［J］. 數學教育學報，2022，31（03）：39-44+83.

［8］ 張琥. 新課標高中數學教材習題教學現狀分析與建議［J］. 數學教育學報，2012，21（04）：60-63.

［9］ 陳振宣. 三角函數在中學數學中的核心地位［J］. 數學通報，2009，48（06）：25-30.

［10］ 鄭蕾，雷浩. 美國“實施課程調查”項目進展及運作機制——SEC項目主任約翰·史密森博士專訪［J］. 全球教育展望，2017，46（10）：11-23.

［11］ 喻平. 數學核心素養評價的一個框架［J］. 數學教育學報，2017，26（02）：19-23+59.

［12］ Porter A C. Measuring the Content of Instruction： Uses in Research and Practice［J］. Educational Resear[-]cher，2002，31（07）：3-14.

［13］ 王彥棋，石玲瑜. 基于數學學科核心素養的普通高中數學教科書與課程標準比較分析——以人教A版中的“函數”習題為例［J］. 遼寧師專學報（自然科學版），2021，23（03）：1-7.

［14］ Fulmer G W.Estimating Critical Values for Strength of Alignment Among Curriculum， Assessments， and instruction［J］. Journal of Edu[-]cational and Behavioral Statistics，2011，36（6）：381-402.

［15］ 孔凡哲. 完善基礎教育課程標準的若干思路——來自中小學教科書實驗的啟示［J］. 教育研究，2008，（04）：56-62.