利用GeoGebra軟件輔助理解關聯速度模型

摘 要：在高中物理教學中，“關聯速度模型”是教學難點和易錯點，其復雜抽象的關聯運動情境更適合用動態化教學軟件展示，從而更好地幫助學生理解運動的合成與分解規律。本文借助GeoGebra軟件構建動態關聯速度模型，可以定量化、動態化、可視化地展示關聯速度模型中的物體運動和速度的合成與分解關系，幫助學生深刻理解運動的合成與分解原理，有效地突破教學難點。

關鍵詞：中學物理；運動的合成與分解；可視化教學

針對“運動的合成與分解”一節，《普通高中物理課程標準（2017年版2020年修訂）》要求：“體會將復雜運動分解為簡單運動的物理思想。”“關聯速度模型”作為運動的合成與分解的典型應用，是高中物理教學中的難點，也是高考的熱點問題。［1］關聯速度模型就是將兩個物體通過不可變形的輕繩、輕桿或直接接觸發生聯系，求兩物體速度之間的關系。兩物體的速度通常不同，但存在某種聯系，這就是關聯速度。［2］關聯速度分析的關鍵在于分清物體之間的速度關系，找出合運動和分運動。合運動是由各分運動共同產生的總運動效果，合運動與各分運動的總運動效果可以相互替代。［3］傳統教學中常用的板書很難直觀地展示關聯速度模型中的動態速度關系，更難使學生構建出真實的物體運動圖像。若能把物體運動時的速度情況動態化地演示出來，則能夠很好地幫助學生理解這一物理規律。GeoGebra軟件是一款數形結合軟件，能夠對物理過程、物理模型進行模擬，將抽象的物理運動情境定量化、可視化、動態化。［4］本文借助GeoGebra軟件構建動態關聯速度模型，展示物體在運動過程中的“關聯速度”問題和速度變化關系，定量、直觀地顯示合速度與分速度之間的關系，幫助學生理解該類問題，建立正確的運動觀，有效解決教學難點。

1 關聯速度模型總述

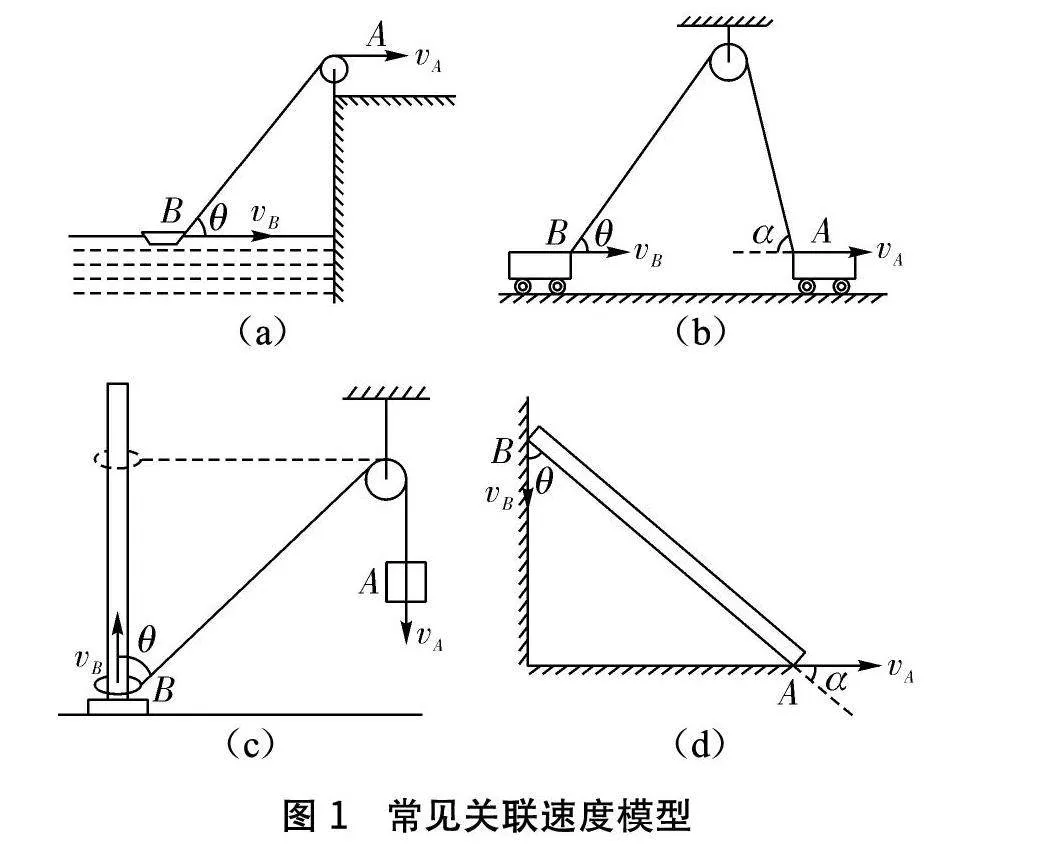
常見的關聯速度模型有繩模型和桿模型，如圖1所示。圖1（a）是繩模型，A端繩子通過定滑輪拉動B端小船，使小船靠岸；（b）是繩模型，A端車通過定滑輪拉動B端車；（c）是繩模型，A端重物通過定滑輪拉動套在豎直細桿上B端的圓環；（d）是桿模型，輕桿兩端分別沿豎直墻面與水平地面滑動。在這類問題中，繩和桿不可變形，摩擦力不計，繩和桿的質量不計。常常已知A端物體的速度vA，求解B端物體的速度vB，α是vA的方向與繩或桿的夾角，θ是vB的方向與繩或桿的夾角（均選取銳角）。

以圖1（a）繩模型的常規教學為例，在岸上以速度vA勻速拉繩子，使小船沿水平面向岸邊靠攏，求B端繩子與水平方向成θ角時，船的速度vB的大小。由于繩子不可伸縮，因此沿繩子方向的速度大小處處相等，即為關聯速度v關。繩子A端的運動是合運動，實際效果是A端沿著繩子運動，其方向即是合速度方向，則v關＝v繩＝vA。

B端小船的運動是合運動，實際效果有兩個，一個是B端沿繩子的運動，另一個是B端繞定滑輪的轉動。因此，將B端小船速度vB分解為沿繩方向的速度v繩（與vB的夾角為θ）和垂直于繩方向、繞定滑輪轉動的速度v轉，如圖2（a）所示。根據三角函數關系，v關＝v繩＝vBcosθ，因此vB＝v繩cosθ＝vAcosθ。

學生在解這類問題時的易錯點如下：①錯誤地判斷合運動和分運動。認為繩子的運動是合運動，B端小船的運動是繩子運動的一個分運動，將v繩按如圖2（b）所示分解，錯誤地得到vB＝v繩cosθ＝vAcosθ。②不能根據合運動的實際效果分解合速度。［5］有的學生雖然能判斷出B端小船的運動為合運動，但在進行速度的分解時，將其分解為沿繩的方向和垂直于船運動的方向的兩個速度，如圖2（c）所示。③受生活經驗的影響。學生容易認為施力物體的運動速度vA應該大于受力物體vB，［6］即vAgt;vB。

為了避免學生分析問題時思路不清晰而導致解題錯誤，根據關聯速度模型的特點，可將關聯速度模型解題分為以下幾個步驟：①確定繩子末端A、B點的合速度（實際速度）的方向，物體實際的運動方向就是合運動的方向，即合速度的方向，即A、B點的合速度分別為vA、vB。②根據合運動的兩個實際效果分解合速度，一個沿繩方向即v關，另一個垂直于繩方向。③利用平行四邊形定則作出A、B兩端各自速度的矢量圖并得到合速度與分速度的關系，v關＝vAcosα、v關＝vBcosθ。④根據關聯速度大小相等，最后確定兩個物體的速度大小關系，vB＝v關cosθ＝vAcosαcosθ。

按照上述步驟分析圖1（b）模型。①繩子末端A、B的合速度均沿水平方向。②將A、B端的合速度分解為沿繩方向和垂直于繩方向的分速度。③A端有v關＝v繩＝vAcosα，B端有v關＝v繩＝vBcosθ。

④vB＝v關cosθ＝vAcosαcosθ。同理，圖1中（c）（d）模型也能根據上述步驟正確求解。

利用上述解題步驟雖然能夠簡單、快速地求解關聯運動的速度，但有些學生空間思維能力較弱，難以理解動態的運動情景，容易機械記憶這種類型題目的解法。因此，為了讓學生更深入理解速度的合成與分解原理，可以使用GeoGebra軟件為學生展示動態關聯速度模型，使其可以定量化地觀察到關聯速度模型中速度的變化情況。

2 利用GeoGebra軟件構建關聯速度模型

以圖1模型中兩端A、B點分別作為研究點，根據v關在GeoGebra軟件中構建圖1的關聯速度動態模型。

首先，創建A點速度vA，vA與繩或桿的初始夾角ω1，B點速度vB，vB與繩或桿的初始夾角ω2，時間t，角度隨時間變化量δ1、δ2的滑動條。

其次，繪制A點的運動及其速度向量：A點位置為（vAt，3），選擇“旋轉”工具構建vA與繩或桿的夾角α＝ω1-δ1，選擇“圓和向量”工具構建A點速度向量vA、分速度向量v關＝vAcosα、v＝vAsinα。

最后，繪制B點的運動及其速度向量：選擇“旋轉”工具構建vB與繩或桿的夾角θ＝ω2＋δ2，根據vB＝v關cosθ＝vAcosαcosθ，B點位置為（vBt，3），選擇“圓和向量”工具構建B點速度向量vB、分速度向量v關＝vBcosθ、v＝vBsinθ。

A點是主動端，B點由于A端的牽連而運動。從合運動和分運動的概念來看，關聯物體發生運動的過程中，與連接物相連接的兩端物體的運動都是合運動，而連接物的運動是分運動，故此時A、B點的運動即為合運動，速度即為物體的速度vA、vB。繩或桿上任意點沿繩或桿方向的速度大小相同，沿著繩或桿的速度就是關聯速度v關。

3 關聯速度模型動態教學展示

GeoGebra軟件能夠通過調節參數展示不同情況下物理量的動態變化過程。啟動動畫，可以清晰地看到運動過程中v關及A、B點的速度vA、vB的大小、方向變化情況。

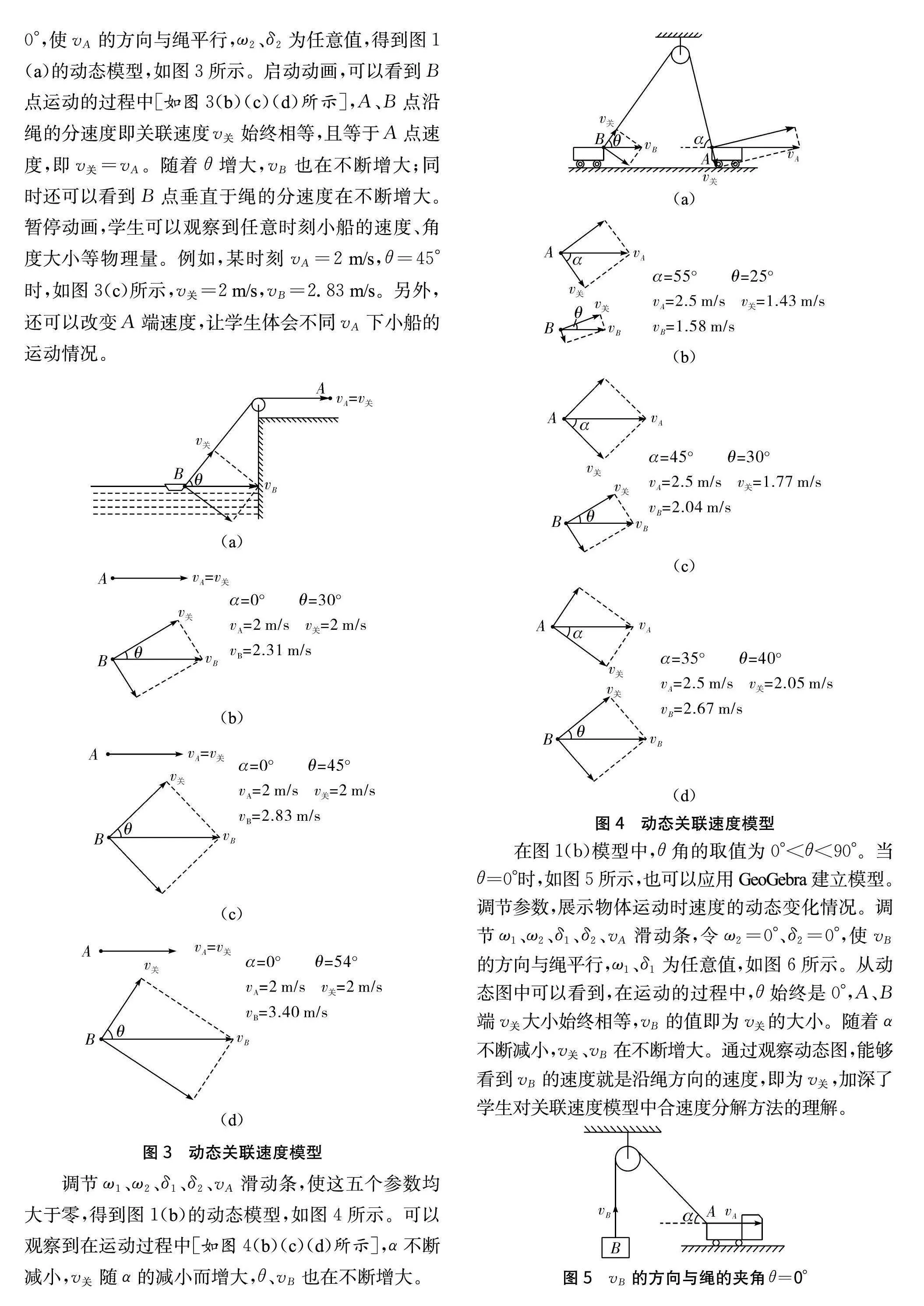
調節ω1、ω2、δ1、δ2、vA滑動條，令ω1＝0°、δ1＝0°，使vA的方向與繩平行，ω2、δ2為任意值，得到圖1

（a）的動態模型，如圖3所示。啟動動畫，可以看到

B點運動的過程中［如圖3（b）（c）（d）所示］，A、B點沿繩的分速度即關聯速度v關始終相等，且等于A點速度，即v關＝vA。隨著θ增大，vB也在不斷增大；同時還可以看到B點垂直于繩的分速度在不斷增大。暫停動畫，學生可以觀察到任意時刻小船的速度、角度大小等物理量。例如，某時刻vA＝2m/s，θ＝45°時，如圖3（c）所示，v關＝2m/s，vB＝2.83m/s。另外，還可以改變A端速度，讓學生體會不同vA下小船的運動情況。

調節ω1、ω2、δ1、δ2、vA滑動條，使這五個參數均大于零，得到圖1（b）的動態模型，如圖4所示。可以觀察到在運動過程中［如圖4（b）（c）（d）所示］，α不斷減小，v關隨α的減小而增大，θ、vB也在不斷增大。

在圖1（b）模型中，θ角的取值為0°lt;θlt;90°。當θ＝0°時，如圖5所示，也可以應用GeoGebra建立模型。調節參數，展示物體運動時速度的動態變化情況。調節ω1、ω2、δ1、δ2、vA滑動條，令ω2＝0°、δ2＝0°，使vB的方向與繩平行，ω1、δ1為任意值，如圖6所示。從動態圖中可以看到，在運動的過程中，θ始終是0°，A、B端v關大小始終相等，vB的值即為v關的大小。隨著α不斷減小，v關、vB在不斷增大。通過觀察動態圖，能夠看到vB的速度就是沿繩方向的速度，即為v關，加深了學生對關聯速度模型中合速度分解方法的理解。

利用GeoGebra軟件展示物體運動速度的動態、可視化關聯速度模型，學生能夠直接觀察到兩個物體運動時A、B端速度矢量發生的變化，［7］建立起物理動態圖像。結合教師的講解，學生可以更加深度的思考，從而真正理解關聯速度模型的解題方法。

4 結語

現代教育技術的應用為高中物理教學帶來了很多便利，許多重要但不容易講透的物理規律可以通過現代技術進行可視化展示，從而糾正學生之前錯誤的觀念，幫助學生在頭腦中構建出物體真實的運動圖像。［8］通過定量化、動態化地展示關聯物體運動過程中的v關、vA、vB等物理量的大小及方向變化情況，使學生能夠理解物體實際的運動是合運動，沿繩或桿的運動是分運動，并且沿繩或桿的速度大小相等，從而正確判斷合運動和分運動。利用動態圖突破了學生的認知難點，［9］使學生能夠懂得按照物體實際運動情況分解合速度，將合速度分解為沿繩或桿方向和垂直于繩或桿的方向上。另外，還能使學生體會到一些直觀上較難想象的關系，如在運動的過程中，vB的速度可以大于vA，即受牽連物體的運動速度是可以大于主動施力物體的。

參考文獻

［1］卓越，姚力.關聯速度的處理方法及應用舉例［J］.物理教師，2011，32（4）：24-25.

［2］張大同.（創新班和理科班用） 物理 （高中上冊）［M］.上海：上海教育出版社，2012：30-31，62.

［3］周凱.用合運動與分運動的關系“三步法”輕松解決繩端速度關聯類問題［J］.湖南中學物理，2014，29（8）：60-61.

［4］丘來金.用GeoGebra輔助探究追擊與相遇的教學［J］.湖南中學物理，2022，37（8）：73-75.

［5］許慶元.繩 桿連結物體的速度求解［J］.物理通報，2016（S1）：107-108.

［6］游才臻.巧探關聯速度問題，建立正確的運動觀——以繩拉小船模型的實驗教學為例［J］.物理教學探討，2021，39（10）：55-56，60.

［7］明翔宇，陳俊.在“雙新”背景下，例談GeoGebra軟件在高中物理教學中的應用［J］.物理教學，2022，44（4）：22-26.

［8］陳林，桑芝芳.基于GeoGebra軟件的磁場動態圓問題的可視化分析——以一道帶電粒子在磁場中運動的多解問題為例［J］.物理教學，2020，42（9）：26-28.

［9］殷正徐，吳偉.GeoGebra軟件在高中物理課堂教學中的應用案例分析——以簡諧振動和機械波為例［J］.物理教師，2017，38（10）：70-73.