穩中求新巧過



1 試題整體分析
2024年普通高等學校招生統一考試全國甲卷(適用省份:陜西、青海、寧夏、內蒙古、四川)是最后一年使用了,該數學試卷充分體現“價值引領、素養導向、能力為主、知識為基”的高考評價理念的同時,試題基于高考評價體系,突出關鍵能力,落實立德樹人,符合基礎性、綜合性、應用性和創新性的高考改革要求.試題穩中求新巧過渡,多思少算考素養,題目難度看似不大,但對理性思維和數學運算素養要求較高,方法選擇不當很難得高分,具體有如下特點.
1.1 結構穩定,巧妙過渡
2024年高考數學全國甲卷的試題結構與2023年的保持一致,體現了“主干知識頻繁考、重點知識重點考”的原則.容易發現,理科的第1,2,3,4,5,6,7,8,13,14,15題(共55分),文科的第1,2,3,4,5,6,7,8,9,13,14,15題(共60分)是基礎題,主要考查基本概念和基本運算;文科和理科的第17,18,19題以及選做題(共46分)是中檔題,重點考查常規的數學運算、數學思想方法和邏輯推理.這些題目加起來有100多分,都是日常教學中重點強調、考前反復訓練的常規問題,考查的都是通性通法,考生只要靈活應用解題技巧,完成這些題目的解答是比較容易的.
尤其是文科和理科第10題,題目以立體幾何的線面位置關系為背景,讓學生選擇出所有真命題的編號,從字面上看是單選題,實質上是多選題,平穩實現了新老高考的巧妙過渡.
1.2 穩中求新,多思少算考素養
本套試卷考查內容嚴格按照課程標準知識范圍命制,強調在深刻理解基礎上融會貫通、靈活應用,考查關鍵能力,不考死記硬背,引導中學教學重點從總結解題技巧轉向培養學生核心素養.盡管試題難度平緩上升,淡化壓軸題概念,不出偏題怪題,但試題注重解決問題要有創新的思想.
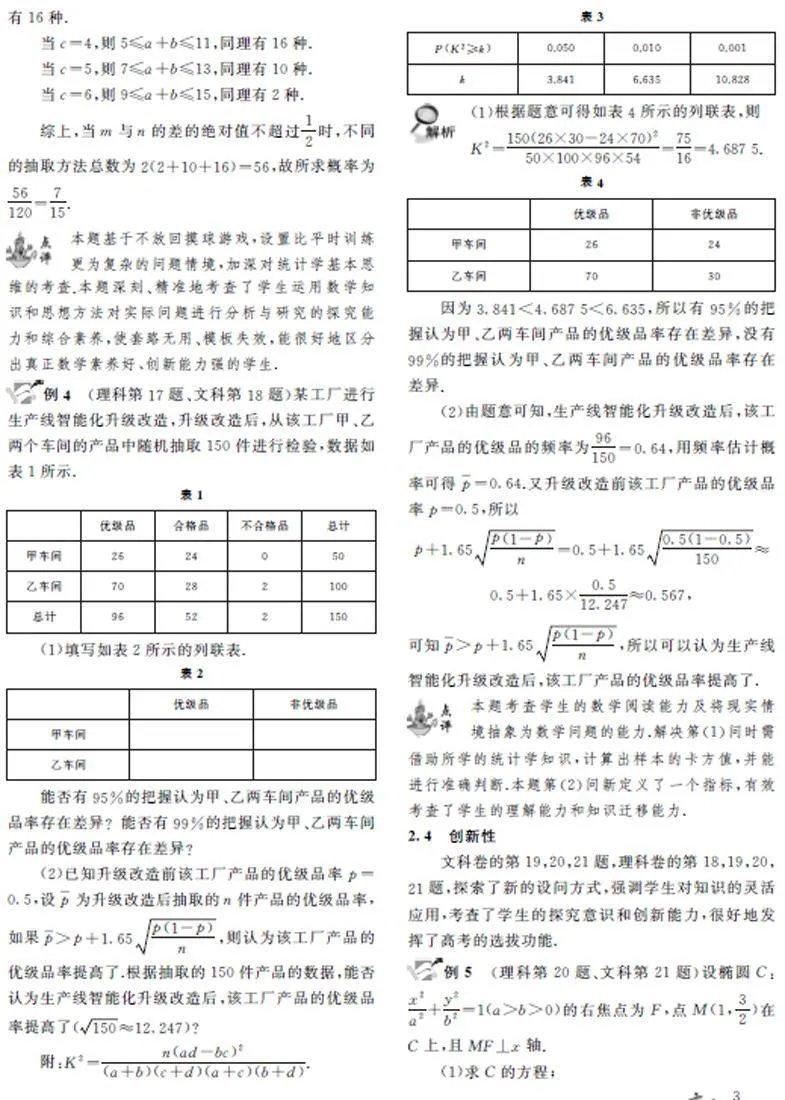
2024年高考數學全國甲卷文科和理科的第5,8,11,12,13,16,18,20,21題,都從理解運算對象、掌握運算法則、探究運算思路、選擇運算方法、設計運算程序、求得運算結果的表現形態對學生進行了全方位的考查,滲透了優化運算方法、簡化運算過程的意識,體現了多思少算考素養的目的.如理科第5題要求考生對雙曲線的基本知識掌握要全面深刻,從點的特殊性出發簡化運算;理科第13題,要避免“小題大做”,可以通過直接觀察、估算快速求出二項式各項系數中的最大值;理科第16題,基于不放回摸球游戲,設置比平時訓練更為復雜的問題情境,加深學生對統計學基本思維的理解;文科和理科統計解答題的第(2)問,新定義了一個判定指標,考查學生的理解能力和知識遷移能力;理科的數列大題,好多學生看到bn =(-1)n-1nan ,認為求數列{bn}的前n 項和Tn 要分類討論,然而當計算出第(1)問的通項an =4(-3)n-1后,發現求數列{bn }的前n 項和Tn 只需錯位相減法即可.這樣的設計真正實現了反套路、反刷題,打破了固化的定勢思維和應試慣性.試卷許多問題還在多個知識板塊的結合處命題,考查學生對知識的理解和靈活運用能力.
總之,試題的設計具有強烈的時代感和濃厚的生活氣息,體現了數學應用的與時俱進,體現了以學生發展為本、立德樹人、提升素養的基本理念,在體現數學魅力的同時,傳遞了正能量.
2 特色試題賞析
下面筆者以2024年全國甲卷中的部分試題為例,深度探析高考真題,剖析高考試題的特色,總結規律,明晰高考備考方向.
2.1 基礎性
文科卷的第1,2,3,4,5,6,7,8,9,13,14,15,17,18,19題,理科卷的第1,2,3,4,5,6,7,8,13,14,15,17,18,19題,全面系統地考查了高中數學核心概念、基本原理、基本方法,考查學生是否掌握了必備的基礎知識,是否形成了解決問題的關鍵能力.
點評
本題第(2)問的設問方式是證明AQ ⊥y 軸,與以往證明定點、定值等問題不同,給考生耳目一新的感覺,主要考查非對稱的根與系數關系的應用,突破難點在于合理轉化,巧妙消參,入口寬,深入難,若方法選擇不當,運算量就很大.本題為學生提供了廣闊的思維空間,很好地考查了學生的探究能力和創新意識.
3 高考復習備考策略
3.1 立足課程標準,培養關鍵能力
?普通高中數學課程標準(2017年版2020年修訂)?是高考數學考查內容范圍和考查要求層次的依據,?中國高考評價體系?是高考數學命題理念的依據,高考備考要以?中國高考評價體系?為指導,以數學課程標準為依據,明確“基礎性、綜合性、應用性,創新性”的考查要求,遵循數學復習規律,把握高考命題方向,注重建構數學知識網絡,完善認知結構,夯實必備知識,優化學科素養,提升關鍵能力.
3.2 回歸教材,夯實“四基”
在復習備考過程中,教師要特別注重對教材的使用.作為高考命題的重要參考之一,教材在復習備考中具有不可替代的作用,師生要利用好教材的引領功能,在重視教材例題的過程中規范解題的步驟與答題格式,在練習教材重點習題的過程中夯實通性通法.同時,要關注教材內容的變化,注重概念的對比辨析,增強對知識網絡的辨識能力.通過具體實例,經歷問題解決的過程,準確構建知識體系.
高考備考要聚焦內容考查主線,精心設計復習計劃,以問題情境引導學生積累知識,建構知識聯系,注重通性通法,夯實必備知識,幫助學生深度理解核心概念、數學思想和方法,完善數學認知結構,提升數學核心素養.
3.3 關注知識生成過程,提升數學核心素養
數學高考題通過命題創新,提高試題的靈活度,突出考查學生的理性思維和探究能力,打破了固化的定勢思維和應試慣性,教師要重視情境創設,引導學生關注知識的生成過程,引導學生通過觀察、思考、探究,提高發現問題、提出問題、分析問題和解決問題的能力;引導教學關注思維的深刻性,通過問題引導、點撥啟發和深化提升,促進學生學會思考、拓展思維,培養學生在學習中做到舉一反三,從而提升學生的數學核心素養.
3.4 注重日常積累,提升數學運算素養
注重日常積累,提升數學運算素養?普通高中數學課程標準(2017年版2020年修訂)?把數學運算作為數學學科核心素養之一,顯現出數學運算在高中數學學習中的重要性,可是在高考中學生經常出現“會而不對,對而不全,全而不優”的現象.基于對2024年高考數學全國甲卷試題中部分典型題目的解析,筆者對高三一輪復習關于提升學生數學運算素養的策略提出如下教學建議.一是要規范運算思路和步驟,養成正確的思維邏輯習慣.
二是在運算量較大的專題中,進行“互助練習”“師生同題友好賽”等活動,浸潤式展示運算原生態場景,展示從分析條件、構建思路、選擇和調整運算程序、確定具體方法和運用,尤其是包括具體數字運算在內的特色性解題過程的練習.
三是提升學生的自信心,重視對學生運算能力的反思和評價,探究提升數學運算能力的有效方法.四是積累,數學運算由能力上升到素養,離不開對基礎知識、基本方法及基本題型的積累和對基本活動經驗的積淀.數學運算實際上是對基礎知識、基本方法、基本經驗的系統考查,任何一個出了問題,都會導致運算結果出錯,因此要想真正提升數學運算素養就必須積累好基礎知識、基本方法和基本題型等.
2024年高考數學全國甲卷試題積極貫徹?中國高考評價體系?要求,加大試題的創新力度,考查數學學科核心素養和關鍵能力,發揮高考的選拔功能.在新一屆的數學教學與高考復習備考中,要注重引導學生經歷數學知識的發生發展過程,以及問題的發現、提出、分析和解決的過程,充分挖掘典型問題的內在價值與遷移功能,培養學生思維的靈活性與創新性.
(完)

