基于圖示法的線性代數教學研究與實踐

摘要：“線性代數”是一門面向低年級非數學專業(yè)大學生的核心基礎課，在現代科學技術的各個領域都有著十分廣泛的應用，對學生后續(xù)專業(yè)課程的學習起到重要作用。然而抽象的概念符號以及繁多的公式性質使得學生難以抓住知識的本質，疲于死記硬背，導致學習興趣和熱情降低，為學生學好這門課帶來了不小的阻礙。本文圍繞線性空間和線性變換這兩個線性代數知識體系中的重要概念，研究利用圖示教學法直觀形象地解釋符號背后所蘊含的知識邏輯。通過圖示展示概念之間的所屬關系，刻畫線性空間及其子空間的結構和相互關系，幫助學生更容易地理解抽象的概念，更深入地掌握知識要點，培養(yǎng)學生的形象思維能力，進而激發(fā)學習興趣，提高學習效率，達到提升課程的教學質量和效果的目標。

關鍵詞：線性代數；圖示教學法；形象化思維

中圖分類號：G642文獻標識碼：A

“線性代數”是高等院校開設的一門面向非數學類專業(yè)的核心基礎課，在現代科學技術的各個領域有著十分廣泛的應用，瑞典科學家L.戈丁曾說：“如果不熟悉線性代數的概念，就去學習自然科學，現在看來就和文盲差不多，甚至可能學習社會科學也是如此。”［1］因此，讓剛進入大學校園的學生能夠“學好線性代數”是高等教育階段的一項重要任務。然而，由于線性代數概念本身具有較強的抽象性，相比于微積分等數學學科，更加強調概念和性質的解釋和關聯，學生理解起來并不容易，從而導致學習興趣和熱情降低［2，3］。自20世紀80年代以來，圖示教學法開始興起，通過文字、符號、數字等形式構成圖示結構，展示知識框架之間的邏輯關系，因其直觀系統化的特點，能夠大大減少需要傳遞的信息量，提高教學效果和效率，所以被廣泛應用于數學、歷史、地理等各個學科［4］。

本文圍繞線性空間和線性變換這兩個在線性代數知識體系中十分重要的概念［56］，探討如何利用圖示教學法，幫助學生更好地理解知識要點，激發(fā)學生學習興趣，達到提升課程的教學質量和效果的教學目標。

1概念圖示

要準確理解線性代數的概念體系，最重要的一點是厘清概念之間的所屬（包含）關系，下面討論線性空間和線性變換相關概念的圖示設計方法。

1.1線性空間及其基

線性空間本質上是對線性運算封閉的對象的集合，而線性空間的基是其中具有特殊性質的向量組，即基向量之間線性無關，個數固定（為線性空間的維數），線性空間中的任一向量α都可以由基線性表示，并且基不唯一。因此，采用集合論中的文氏圖表示方法，以矩形框（的內部區(qū)域）表示線性空間V（如圖1所示），以大小相同的實心圈表示基，不同基之間可能存在公共向量也可能不相交，用箭頭表示前者可由后者線性表示，得到線性空間結構的圖示。

1.2線性空間的子空間

線性空間V的子空間是V中對線性運算封閉的子集。每個子空間都可以看作是由其基張成的（即由基的所有線性組合構成的）；任一向量組都可以張成一個子空間，若這個向量組線性無關，則它就構成所張成子空間的一組基。因此，同樣采用文氏圖的表達方法，以矩形框（的內部區(qū)域）表示n維線性空間V，設V的一組基為α1，α2，…，αn，以空心圈表示由向量組張成的子空間，則由基向量張成的子空間的結構如圖2所示。進一步假設一個s維子空間W的一組基為β1，β2，…，βs，顯然sn，則向這組基依次添加向量γ1，…，γn-s便可擴充為V的一組基，其中對任意γi（1in-s）都有β1，β2，…，βs，γ1，…，γi線性無關，即γi不屬于β1，β2，…，βs，γ1，…，γi-1所張成的子空間，這一過程如圖2所示。

1.3線性方程組解的結構

以m×n矩陣A為系數矩陣的齊次線性方程組Ax=0的解集構成n維向量空間的子空間，故可稱為解空間，其一組基稱為該齊次線性方程組的基礎解系，不妨設為ξ1，ξ2，…，ξt；非齊次線性方程組Ax=b的解集由于不含零向量，因此并不構成向量空間，但其通解可表示為x=η+k1ξ1+k2ξ2+…+ktξt，其中η為Ax=b的一個特解，k1，…，kt取任意數，即Ax=b的所有解就是將Ax=0的每個解與η求和得到，因此兩個解集的大小（當解集為無限集時即為勢）相同，在幾何上Ax=b的解集即是將Ax=0的解空間平移η。因此，以兩個大小相同的空心圈分別表示Ax=0的解空間和Ax=b的解集，箭頭表示解向量之間的對應關系（如圖3所示）。

1.4歐氏空間的基、線性變換及其矩陣

由于歐氏空間是在線性空間上引入了內積運算，因此若在基向量之間線性無關的基礎上進一步要求基向量之間相互正交，則可得到正交基，更進一步要求每個基向量均為單位向量便可得到標準正交基。線性變換在一一映射的條件下即為可逆變換，若進一步要求保持向量長度不變則為正交變換，更進一步要求對空間中所有向量繞某個向量旋轉某個角度即為旋轉變換，而對稱變換則以上情況都有可能。由于在給定一組基下，任一線性變換都與一方陣相互確定，因此方陣也相應地分為可逆陣、正交陣、旋轉矩陣和實對稱陣。但是需要強調的是，在任何一組基下，可逆變換與可逆陣可以相互確定，但只有在標準正交基下，正交變換才與正交陣相互確定，旋轉變換才與旋轉矩陣相互確定，對稱變換才與實對稱陣相互確定。因此，分別以大小包含的空心圈表示概念之間的所屬關系，得到相關的概念體系如圖4所示。

2性質圖示

2.1線性空間的維數公式

設V1，V2是線性空間中的兩個子空間，則有dimV1+dimV2=dim（V1+V2）+dim（V1∩V2）.此維數公式本質上刻畫了子空間V1的基、V2的基、V1∩V2的基與V1+V2的基之間的構成關系。以兩個空心圈分別表示子空間V1和V2（如圖5所示），這兩個圈重疊的區(qū)域即表示V1∩V2，以含有這兩個實心圈的矩形框（的內部區(qū)域）表示V1+V2，以一個實心圈表示V1∩V2的一組基S。由于V1∩V2為V1的子空間，所以由S可以擴充為V1的一組基，不妨設添加的向量組為T，以一個實心圈表示，顯然TV1并且T中任一向量都不屬于V1∩V2；同理，由S可以擴充為V2的一組基，不妨設添加的向量組為G，以一個實心圈表示，顯然GV2并且G中任一向量都不屬于V1∩V2，則這三個實心圈的并S∪T∪G即構成V1+V2的一組基。

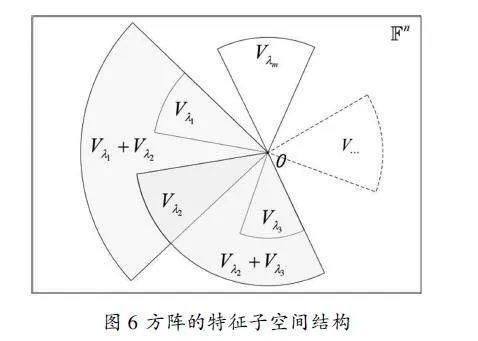
特別地，若V1∩V2=0，則S為空集，T即為V1的一組基，G即為V2的一組基，這時V1與V2之和為直和。例如，設n階方陣有m個不同的特征值λ1，…，λm，每個特征值λi都確定一個特征子空間Vλi，由于屬于不同特征值的特征向量線性無關，所以特征子空間之和也為直和，故Vλ1∩Vλ2∩…∩Vλm=0。以矩形框（的內部區(qū)域）表示特征向量所屬的向量空間Fn（如圖6所示），以只有一個公共頂點（零向量）的空扇面表示特征子空間Vλ1，Vλ2，…，Vλm以及Vλ1+Vλ2，Vλ2+Vλ3等和空間。由于特征子空間之間為直和，所以有（Vλ1+Vλ2）∩（Vλ2+Vλ3）=Vλ2。

2.2線性變換的維數公式

設σ為n維線性空間V上的線性變換，則有dimσ-1（0）+dimσ（V）=n.其中σ-1（0）為線性變換的核空間，σ（V）為線性變換的值域。此維數公式本質上刻畫了核空間的基與值域的基之間的關系。以兩個大小相同的矩形框（的內部區(qū)域）分別表示線性空間V（如圖7所示），從左至右的箭頭表示在線性變換σ作用下的映射關系。在左側矩形框中以空心圈表示核空間，其一組基T以實心圈表示，以一點表示零向量；在右側矩形框中以小矩形框表示值域，其一組基S以實心圈表示，以一點表示零向量。從核至零向量加以箭頭表示σ將核中所有向量都映射為零向量。在左側矩形框中以與基S同樣大小的實心圈表示基S的原象，表示這兩組向量個數相同，并以箭頭連接表示σ將基S的原象中的每個向量都映射為基S中的對應向量，則值域的基S的原象與核的基T之并即構成V的一組基。由此可知，核越“小”則值域越“大”，但兩者的維數之和始終不變。特別地，若核空間縮小到只含有零向量，則基T為空集，值域即為V，這時的線性變換為一一映射，故為可逆的線性變換。

3教學效果

文中所述圖示，筆者已在北京航空航天大學“工科高等代數”教學中進行了實踐，從2023年秋季學期筆者的教學班的問卷調查結果來看，同學們對圖示教學法持積極肯定的態(tài)度，能夠促進對知識的學習和理解。

結語

“線性代數”知識的抽象性是學生學習的難點，為了幫助同學更形象地理解知識要點，本文提出利用圖示教學法，展示了如何將線性空間和線性變換相關的概念定義和性質從文字表述轉化為圖示形式，直觀系統地呈現知識邏輯關系，并通過課堂實踐表明圖示教學法有利于培養(yǎng)學生的形象思維能力，激發(fā)學生的學習興趣，提高學習效率，從而達到提升課程的教學質量和效果的目標。

參考文獻：

［1］L.戈丁.數學概觀［M］.胡作玄，譯.北京：科學出版社，2001.

［2］李良，黃廷祝，程光輝.喚起好奇，激發(fā)志趣——在線性代數課程中融入計算思維［J］.大學數學，2022，38（4）：4043.

［3］車國鳳，張麗麗.“線性代數”教學改革的思考與實踐［J］.教育教學論壇，2022（28）：98101.

［4］李夢瑤.圖示教學法在初中歷史教學中的運用研究［D］.上海：上海師范大學，2021.

［5］李尚志.線性代數［M］.北京：高等教育出版社，2011.

［6］高宗升，周夢，李紅裔.線性代數（第3版）［M］.北京：北京航空航天大學出版社，2016.

基金項目：2023年北京航空航天大學一流本科課程立項項目“工科高等代數”

作者簡介：陳肖宇（1982—），男，漢族，遼寧沈陽人，博士，講師，碩士生導師，研究方向為數學知識管理和教育數學。