初中數(shù)學(xué)實(shí)驗(yàn)設(shè)計(jì)的范式研究

[摘 要] 數(shù)學(xué)實(shí)驗(yàn)具有工具性、操作性、情境性與探究性等特征，將數(shù)學(xué)實(shí)驗(yàn)有機(jī)地滲透在初中數(shù)學(xué)教學(xué)中，可讓學(xué)生經(jīng)歷知識(shí)的抽象與建模等過程. 數(shù)學(xué)實(shí)驗(yàn)包括驗(yàn)證型、探索型、理解型. 文章針對(duì)這三種類型的數(shù)學(xué)實(shí)驗(yàn)設(shè)計(jì)的范式展開分析.

[關(guān)鍵詞] 數(shù)學(xué)實(shí)驗(yàn);驗(yàn)證型;探索型;理解型;研究

隨著數(shù)學(xué)教育教學(xué)的改革與發(fā)展，如今的數(shù)學(xué)教學(xué)模式發(fā)生了翻天覆地的變化，數(shù)學(xué)教學(xué)不再是單純地為了升學(xué)考試，更重要的是借助教學(xué)滲透數(shù)學(xué)文化，發(fā)展學(xué)生的數(shù)學(xué)思維，提升學(xué)生的數(shù)學(xué)核心素養(yǎng). 數(shù)學(xué)實(shí)驗(yàn)作為轉(zhuǎn)變學(xué)習(xí)方式的重要教學(xué)模式，對(duì)培養(yǎng)學(xué)生的學(xué)習(xí)興趣，提升學(xué)生的探索欲，發(fā)展學(xué)生的綜合素養(yǎng)具有其他教學(xué)方法無(wú)可替代的作用.

數(shù)學(xué)實(shí)驗(yàn)的特征

1. 工具性特征

數(shù)學(xué)實(shí)驗(yàn)的工具性特征主要體現(xiàn)在實(shí)驗(yàn)過程中需應(yīng)用剪刀、紙張、測(cè)量工具、模型、計(jì)算機(jī)等. 而思維實(shí)驗(yàn)卻不需要應(yīng)用任何實(shí)質(zhì)性的輔助工具，僅需人腦對(duì)數(shù)學(xué)事物進(jìn)行信息加工，如假設(shè)、辨析、推斷、概括等. 鑒于操作具體的工具需要應(yīng)用到思維，因此數(shù)學(xué)實(shí)驗(yàn)過程包含了大量的數(shù)學(xué)思維. 數(shù)學(xué)思維是在學(xué)生的手腦并用中形成的.

2. 操作性特征

學(xué)生是實(shí)驗(yàn)的主體，他們通過自主操作去探索問題與領(lǐng)悟本質(zhì)，因此數(shù)學(xué)實(shí)驗(yàn)過程屬于“做中學(xué)”的范疇. “做”是一種發(fā)自學(xué)生主體的行為，具有操作性特征，其成效通過學(xué)生的具體操作來體現(xiàn).

3. 情境性特征

課堂中的數(shù)學(xué)實(shí)驗(yàn)一般置于某種情境中，人的思維、認(rèn)知與學(xué)習(xí)都離不開情境的支撐，學(xué)習(xí)基于情境來實(shí)現(xiàn). 從某種意義上來講，課堂中不存在非情境化的學(xué)習(xí). 因此，數(shù)學(xué)實(shí)驗(yàn)是情境認(rèn)知理論的實(shí)踐，具有典型的情境性特征.

4. 探究性特征

數(shù)學(xué)教學(xué)是學(xué)生探索知識(shí)的過程，數(shù)學(xué)實(shí)驗(yàn)就是學(xué)生通過自主實(shí)驗(yàn)去觀察、思考、分析與類比推理，在“做中學(xué)”中揭示知識(shí)本質(zhì)，提煉數(shù)學(xué)思想方法. 這種教學(xué)模式一改傳統(tǒng)的“先學(xué)后做”“嘗試教學(xué)”等常規(guī)模式，從本質(zhì)上來說，數(shù)學(xué)實(shí)驗(yàn)屬于“再創(chuàng)造”與發(fā)現(xiàn)式的教學(xué)[1].

數(shù)學(xué)實(shí)驗(yàn)設(shè)計(jì)的范式

數(shù)學(xué)實(shí)驗(yàn)是以數(shù)學(xué)問題為出發(fā)點(diǎn)，利用多種手段與工具，借助數(shù)學(xué)思維去探究的一種實(shí)踐活動(dòng). 根據(jù)數(shù)學(xué)實(shí)驗(yàn)的知識(shí)類別與應(yīng)用工具等，可將初中數(shù)學(xué)實(shí)驗(yàn)分為驗(yàn)證型、探索型、理解型三種類型，而每一類型都有特定的結(jié)構(gòu).

1. 驗(yàn)證型數(shù)學(xué)實(shí)驗(yàn)

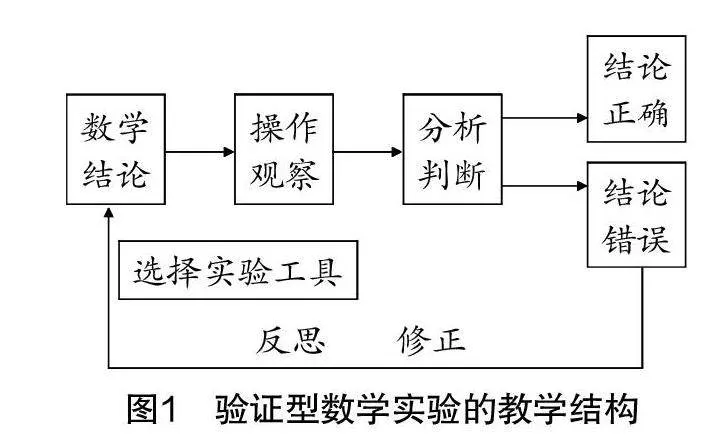
驗(yàn)證型數(shù)學(xué)實(shí)驗(yàn)是指學(xué)生通過自主操作、模型的觀察與分析等手段，檢驗(yàn)自己的猜想是否正確. 如圖1，這種類型的數(shù)學(xué)實(shí)驗(yàn)，學(xué)習(xí)者一般從猜想或結(jié)論出發(fā)，借助數(shù)學(xué)技術(shù)工具或?qū)嵨锬Ｐ偷龋ヲ?yàn)證猜想正確與否. 因此，這是一種歸納與演繹有機(jī)融合的認(rèn)知方式，具有思維起點(diǎn)低、操作簡(jiǎn)便、過程明了等特點(diǎn).

從認(rèn)知心理學(xué)出發(fā)，這一類型的數(shù)學(xué)實(shí)驗(yàn)主要由學(xué)生自主操作實(shí)驗(yàn)工具，通過觀察實(shí)驗(yàn)現(xiàn)象對(duì)結(jié)論形成感性認(rèn)識(shí)，并在此基礎(chǔ)上進(jìn)行理性分析，對(duì)結(jié)論形成準(zhǔn)確的判定. 實(shí)驗(yàn)過程中若出現(xiàn)錯(cuò)誤，可通過實(shí)驗(yàn)反思或再次實(shí)驗(yàn)的方式，更正、完善猜想與結(jié)論.

案例1 “完全平方公式”的驗(yàn)證實(shí)驗(yàn)

當(dāng)學(xué)生獲得完全平方公式后，教師可通過拼圖活動(dòng)的安排，幫助學(xué)生從圖形面積關(guān)系的角度來驗(yàn)證該公式，為形成幾何直觀奠定基礎(chǔ). 而后，通過代數(shù)的運(yùn)算、數(shù)學(xué)推理與變式訓(xùn)練等方式來證明公式，讓學(xué)生對(duì)公式形成客觀、理性的認(rèn)識(shí).

實(shí)驗(yàn)?zāi)康? 讓學(xué)生親歷拼圖活動(dòng)過程，在操作中觀察、交流，驗(yàn)證完全平方公式，滲透數(shù)形結(jié)合思想，發(fā)展幾何直觀.

實(shí)驗(yàn)準(zhǔn)備 邊長(zhǎng)為a，b的正方形紙各1張，2張長(zhǎng)、寬分別為a，b的長(zhǎng)方形紙.

實(shí)驗(yàn)過程

（1）將準(zhǔn)備好的四張紙拼在一起，形成大正方形;

（2）從不同的角度來表達(dá)所拼成大正方形的面積，形成一個(gè)等式.

論證結(jié)論 用代數(shù)運(yùn)算的方法來論證以上實(shí)驗(yàn)所獲得的等式.

應(yīng)用分析 用所獲得結(jié)論來計(jì)算（2a+b）2，并用拼圖法驗(yàn)證該式子的計(jì)算結(jié)論是否正確.

縱觀整個(gè)實(shí)驗(yàn)過程，教師安排學(xué)生用拼圖法來驗(yàn)證完全平方公式，而后在代數(shù)推理論證中明確所獲得公式的正確性. 應(yīng)用分析環(huán)節(jié)，讓學(xué)生充分感知到應(yīng)用完全平方公式計(jì)算的方便，并通過實(shí)驗(yàn)的直觀性闡釋代數(shù)結(jié)論的正確性. 學(xué)生在此過程中，既理解了完全平方公式的多元聯(lián)系，又深化了對(duì)公式的認(rèn)識(shí)，激發(fā)了學(xué)習(xí)興趣.

2. 探索型數(shù)學(xué)實(shí)驗(yàn)

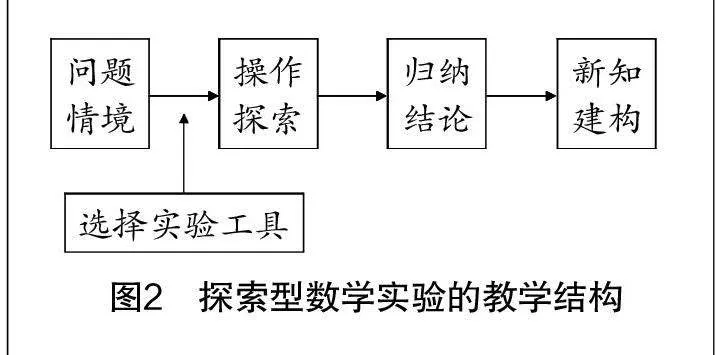
探索型數(shù)學(xué)實(shí)驗(yàn)是指教師通過創(chuàng)設(shè)問題情境，引導(dǎo)學(xué)生借助動(dòng)手操作、觀察、類比、分析、歸納等方式發(fā)現(xiàn)新結(jié)論，該過程具有開放性、探索性等特征，課堂生成度較高[2]. 如圖2，探索型實(shí)驗(yàn)結(jié)構(gòu)一般遵循如下規(guī)律.

探索型實(shí)驗(yàn)首先要問題具備探索價(jià)值，常見的如某種問題所蘊(yùn)含的數(shù)學(xué)原理、思想方法及可推廣的結(jié)論等. 設(shè)計(jì)實(shí)驗(yàn)時(shí)，教師可從問題情境出發(fā)，將學(xué)生置于問題情境中借助實(shí)驗(yàn)工具動(dòng)手實(shí)操，并在觀察與思考中進(jìn)行感知與分析，初步獲得結(jié)論. 探索型數(shù)學(xué)實(shí)驗(yàn)的目的在于發(fā)現(xiàn)新的結(jié)論，這是建構(gòu)新知的基礎(chǔ).

從認(rèn)知發(fā)展規(guī)律出發(fā)，學(xué)生在教師的引導(dǎo)下利用實(shí)驗(yàn)工具進(jìn)行圖形變化、數(shù)值運(yùn)算與動(dòng)態(tài)演示等，通過觀察實(shí)驗(yàn)現(xiàn)象去分析、類比、總結(jié)、提煉出相應(yīng)的結(jié)論，由此也能追溯到一些數(shù)學(xué)知識(shí)所蘊(yùn)含的數(shù)學(xué)思想方法的源頭，這一切可為學(xué)生后續(xù)利用相應(yīng)的結(jié)論進(jìn)行論證推理、理解與掌握知識(shí)提供幫助.

案例2 “一次函數(shù)”的圖象探究

想要認(rèn)識(shí)一個(gè)函數(shù)，首先就要研究它的圖象與性質(zhì)，讓學(xué)生從“數(shù)”與“形”的聯(lián)系中發(fā)現(xiàn)函數(shù)的本質(zhì)，這也是函數(shù)教學(xué)的主線. 函數(shù)圖象作為研究的基礎(chǔ)內(nèi)容，可暴露函數(shù)的性質(zhì).

整個(gè)函數(shù)大家族中，一次函數(shù)是最基礎(chǔ)的內(nèi)容，對(duì)學(xué)生的掌握程度要求較高. 然而，學(xué)生在學(xué)習(xí)一次函數(shù)時(shí)，總是難以真正理解一次函數(shù)為一條直線. 為此，筆者借助幾何畫板的繪圖功能開展數(shù)學(xué)實(shí)驗(yàn)，引導(dǎo)學(xué)生探尋一次函數(shù)圖象.

實(shí)驗(yàn)?zāi)康? 借助幾何畫板的演示功能，揭示一次函數(shù)對(duì)應(yīng)坐標(biāo)點(diǎn)的分布規(guī)律，為獲得“一次函數(shù)圖象為直線”的結(jié)論奠定基礎(chǔ).

實(shí)驗(yàn)準(zhǔn)備 幾何畫板.

實(shí)驗(yàn)過程

（1）教師呈現(xiàn)一次函數(shù)y=2x+1，任意取幾個(gè)x，y對(duì)應(yīng)值的點(diǎn)，將這些點(diǎn)繪制在幾何畫板上，要求學(xué)生自主觀察，說說自己的發(fā)現(xiàn)，并分析函數(shù)y=2x+1的圖象可能是一個(gè)怎樣的圖形.

（2）借助幾何畫板繪制線段AB，讓其與x軸平行，將點(diǎn)A固定在y軸上，讓點(diǎn)B作為動(dòng)點(diǎn)，選中點(diǎn)B的橫坐標(biāo)作為參數(shù)（x），繪制出點(diǎn)P（x，2x+1），拖動(dòng)點(diǎn)B，追蹤點(diǎn)P，對(duì)點(diǎn)P的運(yùn)動(dòng)路徑談一些看法.

（3）要求學(xué)生任選一個(gè)一次函數(shù)，并借助幾何畫板來呈現(xiàn)該函數(shù)的圖象，與同學(xué)交流自己的發(fā)現(xiàn)與看法.

（4）仿照以上實(shí)驗(yàn)過程（2），借助幾何畫板構(gòu)造參數(shù)x與x，并繪制函數(shù)y=kx+b的圖象. 通過對(duì)k的拖動(dòng)，來觀察函數(shù)圖象的變化規(guī)律.

以上為教師針對(duì)學(xué)情與教情設(shè)計(jì)的一個(gè)由具體到抽象的問題情境，學(xué)生借助幾何畫板的繪圖功能，描出一次函數(shù)y=2x+1任意幾個(gè)對(duì)應(yīng)值的點(diǎn)，并從這些點(diǎn)的分布情況分析出該函數(shù)圖象為一條直線. 同時(shí)借助幾何畫板的追蹤功能，發(fā)現(xiàn)點(diǎn)P（x，2x+1）的路徑（直線）. 至此，學(xué)生對(duì)一次函數(shù)的圖象為一條直線已經(jīng)有了初步認(rèn)識(shí).

基于以上探索活動(dòng)，教師要求學(xué)生自主給定一個(gè)一次函數(shù)，并探索它的圖象，操作發(fā)現(xiàn)所獲得的圖象依然是一條直線. 此時(shí)，學(xué)生對(duì)自己的猜想有了更大的信心. 結(jié)合從特殊到一般的數(shù)學(xué)思想，教師要求學(xué)生繼續(xù)引用幾何畫板研究y=kx+b的一般形式，進(jìn)一步確認(rèn)“一次函數(shù)的圖象為一條直線”的結(jié)論.

在以上探索型數(shù)學(xué)實(shí)驗(yàn)中，學(xué)生親歷了從特殊到一般的研究過程. 圖象的特征由學(xué)生親自發(fā)現(xiàn)，這不僅有效培養(yǎng)了學(xué)生動(dòng)手、動(dòng)腦的能力，還增強(qiáng)了學(xué)生的創(chuàng)造力. 因此，探索型數(shù)學(xué)實(shí)驗(yàn)是培養(yǎng)學(xué)生數(shù)學(xué)能力的重要方法之一，對(duì)發(fā)展與培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)具有重要意義.

3. 理解型數(shù)學(xué)實(shí)驗(yàn)

理解型數(shù)學(xué)實(shí)驗(yàn)是指借助模型、實(shí)物或技術(shù)工具等干預(yù)實(shí)驗(yàn)對(duì)象，以利于學(xué)生更好地展開觀察與測(cè)量，為正確猜想奠定基礎(chǔ). 學(xué)生觀察這一類數(shù)學(xué)實(shí)驗(yàn)，從中發(fā)現(xiàn)一些規(guī)律性的內(nèi)容，感知數(shù)學(xué)知識(shí)的可靠性，在充分認(rèn)識(shí)數(shù)學(xué)方法的前提下理解數(shù)學(xué)思想的現(xiàn)實(shí)背景與抽象過程.

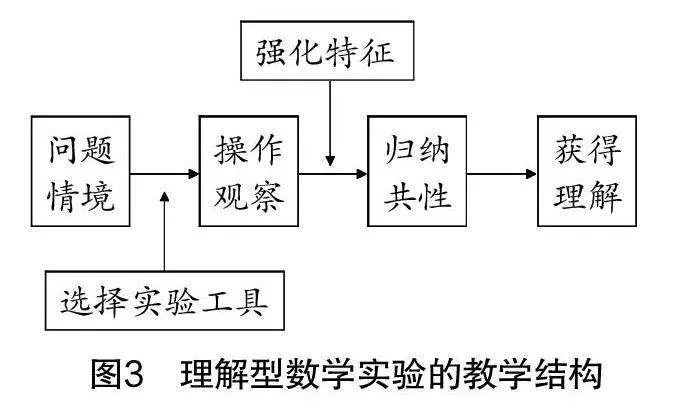
這一類數(shù)學(xué)實(shí)驗(yàn)的最大特點(diǎn)在于操作簡(jiǎn)便、貼近生活、生動(dòng)且高效，如圖3所示，理解型數(shù)學(xué)實(shí)驗(yàn)的教學(xué)結(jié)構(gòu)一般遵循此類規(guī)律.

理解型數(shù)學(xué)實(shí)驗(yàn)一般針對(duì)一些學(xué)生不容易理解的概念、定理或難以把握的動(dòng)態(tài)變化現(xiàn)象而設(shè)置，它能較完整地反映出這些難點(diǎn)內(nèi)容的具體性質(zhì)，引發(fā)學(xué)生的主動(dòng)觀察與思考[3]. 此類實(shí)驗(yàn)也可借助一定的技術(shù)手段來設(shè)計(jì)動(dòng)態(tài)的情境，學(xué)生親歷操作與實(shí)驗(yàn)過程，深化對(duì)知識(shí)的理解. 具體過程為教師應(yīng)用通俗易懂的語(yǔ)言講解與示范，揭露數(shù)學(xué)特征，學(xué)生模仿操作并觀察，將整個(gè)注意力都集中到具體實(shí)例的共同點(diǎn)上，并在綜合分析、歸納提煉中形成理性思維.

案例3 “無(wú)理數(shù)”的概念教學(xué)

無(wú)理數(shù)對(duì)初中學(xué)生而言，屬于抽象難懂的內(nèi)容之一. 為了讓學(xué)生真正理解什么是無(wú)理數(shù)，并在心理上接受無(wú)理數(shù)為一種實(shí)實(shí)在在的數(shù)，筆者針對(duì)本班學(xué)生的特點(diǎn)，設(shè)計(jì)了理解型數(shù)學(xué)實(shí)驗(yàn).

實(shí)驗(yàn)?zāi)康? 借助實(shí)驗(yàn)活動(dòng)，讓學(xué)生在觀察與計(jì)算過程中感知無(wú)限不循環(huán)小數(shù)的存在性，對(duì)無(wú)理數(shù)的特點(diǎn)形成一定了解，發(fā)展數(shù)感.

實(shí)驗(yàn)準(zhǔn)備 計(jì)算器、直尺、圓規(guī)、骰子.

實(shí)驗(yàn)過程

（1）分別將，，，轉(zhuǎn)化為小數(shù)的形式，觀察小數(shù)點(diǎn)右側(cè)的數(shù)字，找出其中的規(guī)律，形成猜想.

（2）同桌之間進(jìn)行擲骰子、寫數(shù)字的活動(dòng)，即一位學(xué)生擲骰子，同桌在小數(shù)0.3的后面添上骰子的點(diǎn)數(shù). 隨著擲骰子的次數(shù)增加，0.3后面的數(shù)字越來越多，呈現(xiàn)出不斷延伸的趨勢(shì). 思考：①若這樣永無(wú)止境地記錄下去，將會(huì)得到一個(gè)什么樣的數(shù)呢？（無(wú)限小數(shù)）②各組所獲得的數(shù)一樣嗎？③這些小數(shù)有什么規(guī)律或特點(diǎn)嗎？

（3）觀察無(wú)限小數(shù)0.606006000600006…，說說它具備怎樣的規(guī)律. 你能否構(gòu)造一個(gè)與之類似的無(wú)限不循環(huán)小數(shù)？

（4）用計(jì)算器計(jì)算，說說它的近似值，盡可能接近精確值.

（5）借助作圖工具，嘗試在數(shù)軸上探尋出π所對(duì)應(yīng)的點(diǎn).

將分?jǐn)?shù)轉(zhuǎn)化為小數(shù)的實(shí)驗(yàn)中，學(xué)生發(fā)現(xiàn)這些分?jǐn)?shù)可轉(zhuǎn)化成有限小數(shù)或無(wú)限循環(huán)小數(shù);擲骰子、寫數(shù)字的實(shí)驗(yàn)，讓學(xué)生發(fā)現(xiàn)無(wú)限不循環(huán)小數(shù)的存在;求的近似值讓學(xué)生親歷了用有理數(shù)逼近無(wú)理數(shù)的過程;在數(shù)軸上探尋π點(diǎn)，讓學(xué)生進(jìn)一步感知有理數(shù)與無(wú)理數(shù)的關(guān)系，并從數(shù)形結(jié)合的角度體驗(yàn)了什么是無(wú)理數(shù). 因此，這個(gè)實(shí)驗(yàn)有效強(qiáng)化了學(xué)生對(duì)無(wú)理數(shù)的理解與接受程度.

類似于這一類抽象程度高的數(shù)學(xué)概念還有很多，理解型數(shù)學(xué)實(shí)驗(yàn)的介入，可讓學(xué)生在具體的背景中抽象數(shù)學(xué)概念，并通過對(duì)背景素材的描述、預(yù)測(cè)與判斷獲得知識(shí)本質(zhì). 這種方式能幫助學(xué)生化解抽象所帶來的困惑，發(fā)展思維，獲得觸類旁通的能力.

想要讓學(xué)生更好地理解新知，教師在設(shè)計(jì)實(shí)驗(yàn)時(shí)應(yīng)先充分了解學(xué)生的實(shí)際認(rèn)知水平與經(jīng)驗(yàn)，為學(xué)生創(chuàng)設(shè)新舊知識(shí)關(guān)聯(lián)的機(jī)會(huì)，讓新知在舊知的基礎(chǔ)上構(gòu)建、生長(zhǎng)，完善認(rèn)知結(jié)構(gòu).

總之，新課標(biāo)背景下的數(shù)學(xué)教學(xué)不僅僅是為了升學(xué)考試，更重要的是將數(shù)學(xué)文化、思維品質(zhì)、思想方法等滲透到教學(xué)中. 數(shù)學(xué)實(shí)驗(yàn)是實(shí)現(xiàn)這一切的重要手段之一. 根據(jù)不同的教學(xué)內(nèi)容設(shè)置不同的實(shí)驗(yàn)，不僅能深化學(xué)生對(duì)知識(shí)的理解，還能讓學(xué)生在實(shí)操中鍛煉自身的各種數(shù)學(xué)能力，激活思維，挖掘潛能，提升學(xué)習(xí)動(dòng)力，發(fā)展數(shù)學(xué)核心素養(yǎng).

參考文獻(xiàn)：

[1]談建青. 核心素養(yǎng)視角下初中數(shù)學(xué)實(shí)驗(yàn)教學(xué)分析與思考[J]. 中學(xué)教學(xué)參考，2019（11）：28-29.

[2]董林偉. 初中數(shù)學(xué)實(shí)驗(yàn)的理論與實(shí)踐研究[M]. 南京：江蘇鳳凰科學(xué)技術(shù)出版社，2016.

[3]喻平，董林偉. 初中數(shù)學(xué)實(shí)驗(yàn)的本質(zhì)解析[J]. 課程·教材·教法，2016，36（08）：89-95.