HPM視角下“等差數列前n項和公式”的教學

［摘 要］ 因為數列是特殊的函數，所以利用函數思想來解決數列問題很重要. 數列在整個高中數學中占有重要地位，是高中數學的核心知識. 文章在HPM視角下對“等差數列前n項和公式”進行研究，帶領學生在相應數學史的理解下更好地運用相關知識去解決問題.

［關鍵詞］ HPM視角；數列；高中數學教學

《普通高中數學課程標準（2017年版2020年修訂）》中的高中數學課程目標提到，在學習數學和應用數學的過程中，學生能發展數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析等數學學科核心素養［1］. 縱觀高中數學課程新結構，數學文化貫穿始終，成為培養學生數學學科核心素養的有效載體［2］. 數學史作為數學文化不可或缺的一部分，承載著培育和發展學生數學學科核心素養的使命，蘊含著豐富的數學教育價值［3］. HPM視角下的數學教學基本方法就是重構歷史、追求知識自然發生的教學法，即以學生的認知起點出發，凸顯所學知識的必要性，呈現知識的自然發生過程，激發學生的學習動機. 如果一個數學概念、一種思想方法從天而降，那么我們直接相信它必然是不符合歷史的. HPM視角下的等差數列教學可以幫助學生建立完整的知識體系. 數列源于生活，如人口增長率、分期付款、儲蓄等實際問題，利用數學建模的思想將現實生活與數學知識緊密結合，引導學生理解數學源于生活且應用于生活；數學知識與數學史相融合，可以擴寬學生的數學視野，使學生了解不同國家的數學文化.

歷史素材的選取

1. 高斯算法

據說，200多年前，高斯的算術老師提出了這樣一個問題：1+2+3+…+100=？

當其他同學忙于把100個數逐項相加時，10歲的高斯卻用下面的方法迅速算出了正確答案：（1+100）+（2+99）+（3+98）+…+（50+51）=101×50=5050.

高斯的算法解決了等差數列1，2，3，…，100的求和問題，但是將其推廣到解決一般等差數列1，2，3，…，n，…的求和問題時，會發現需要討論項數n的奇偶性.

2. 畢達哥拉斯的三角形數

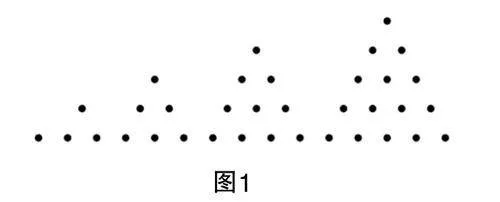
畢達哥拉斯學派在世界數學史上首次建立了數和形之間的聯系，研究過問題1+2+3+…+n=？的幾何表示.早期畢達哥拉斯學派似乎已經熟悉利用小石子或點來構造三角形數、正方形數和長方形數等［4］. 本文中，筆者主要研究三角形數（如圖1所示）.

3. 《九章算術》之“良馬和駑馬”

今有良馬與駑馬發長安至齊，齊去長安三千里，良馬初日行一百九十三里，日增一十三里；駑馬初日行九十七里，日減半里. 良馬先至齊，復還迎駑馬. 問：幾何日相逢及各行幾何？［5］

13世紀中國數學家楊輝在解決《九章算術》中的“良馬和駑馬”問題時，通過構造幾何圖形來求良馬（第一天行193里，以后每天增加13里）和駑馬（第一天行97里，以后每天減少半里）在十五天內走過的路程.用今天的數學語言來表達良馬的行走情形就是：求首項為a（a>0），公差為d（d>0）的等差數列的前n項和，可構造長分別為a，a+d，a+2d，…，a+（n-1）d，寬均為1的n個長方形，則所得的“階梯形”的面積之和就是所求的等差數列的前n項和［6］.

4. 《張丘建算經》的第23、22題

（1）今有女子不善織，日減功遲.初日織五尺，末日織一尺，今三十日織訖.問織幾何？

（2）今有女善織，日益功疾. 初日織五尺，今一月日織九匹三丈. 問日益幾何？

教學過程的設計

1. 引入歷史，發現公式

師：200多年前，高斯的算術老師提出一個問題：1+2+3+…+100=？高斯如何求解？

生1：（如圖2所示）將1與100配對，將2與99配對，以此類推，共有50組，并且他們的和都是101，結果就是101×50=5050.

師：大家想過為什么要一頭一尾兩兩配對嗎？

生2：因為一頭一尾兩兩配對，原本100個不同的數，就變成了50個相同的數.

師：通過這樣的處理，把一般問題轉化成特殊問題，也就是把不同數的求和問題轉化成相同數的求和問題. 高斯是德國數學家，近代數學的奠基者之一，擁有“數學王子”之稱. 他在天文學、測量學、磁學、光學等領域有杰出貢獻. 現代的尺規作圖也得益于高斯的貢獻.

設計意圖 “高斯問題”在曾經的學習中提到過，其是一個以1為首項，1為公差的等差數列求和問題，由于學生的認知基礎、認知潛能、認知風格等存在差異，此處回顧讓學生清楚“高斯問題”的緣由，以及為本節課教學“等差數列的前n項和”做鋪墊，從而很好地發展學生的邏輯推理、數學運算等核心素養.

師：如圖3所示，你能用算式表示這個幾何圖形嗎？

生3：在右上角加上一個同樣的圖形，將其倒放就可以拼成一個長方形. 和就是長方形的長乘寬再取其一半，也就是長方形面積的一半，即=5050.

師：長方形的長和寬分別代表什么數？

生4：寬100代表100組數，長101代表一組數的和為101，100×101為100組數的和，除以2就得到50組數的和，即1+2+3+…+100的和.

設計意圖 先從“數”的方面分析“高斯問題”的緣由，再從“形”的角度進行分析，引導學生深入理解. 由“數”能夠準確地想到“形”，由“形”能夠聯系到“數”，有助于提升學生的數形結合能力和幾何直觀能力，以及數學抽象和邏輯推理等素養，增強學生運用幾何直觀思考問題的意識，幫助學生在具體情境中感悟事物的本質，為后面的倒序相加法的學習做鋪墊.

師：推廣到n項（如圖5所示），你能計算1+2+3+…+n的和嗎？

生5：1+2+3+…+n=. 類比1+2+3+…+100的和的計算，如圖6所示，在長方形中，一共有n組數，一組數的和為n+1，n（n+1）為n組數的和，除以2就是1+2+3+…+n的和，所以1+2+3+…+n=.

師：看來同學們遷移知識的能力很不錯. 其實，畢達哥拉斯學派在世界數學史上首次建立了數和形之間的聯系. 早期畢達哥拉斯學派似乎熟悉利用小石子或點來構造三角形數、正方形數和長方形數等. 今天我們一起來看一下三角形數. 從1開始，任意多個連續自然數之和構成三角形數，如圖7所示. 畢達哥拉斯學派當時提出的就是在三角形數旁補上一個倒立的三角形數，如圖8所示.

師：我國古代數學家對數列的認識也很早，如《九章算術》《周髀算經》《孫子算經》《張丘建算經》《前漢書》《舊唐書》等著作，都載有許多有趣味的數列問題.

設計意圖 將“特殊”推廣到“一般”，將“已知”推廣到“未知”，帶領學生靈活運用并真正理解高斯的算法，培養學生的邏輯思維能力；使用畢達哥拉斯學派的三角形數，通過數形結合，使得數學問題更加形象化.

2. 邏輯演練，公式證明

師：已知等差數列｛a｝的首項為a，公差為d，你可以求它的前n項和S嗎？

生6：S=a+a+…+a+a.

師：畢達哥拉斯學派通過構造圖形來計算，我們可用數學語言將其表達出來.

S=a+a+…+a+a①.

構造另一個與其相同的等差數列將其“倒置”.

S=a+a+…+a+a② .

將①式和②式相加，得到

2S=[][n對]=n（a+a）③.

所以等差數列｛a｝的前n項和公式為S=④.

師：若一個數列｛a｝中，與首、末項等距的兩項之和等于首、末兩項之和，可把正序的和式與倒序的和式相加，得到一個常數列的和，這一求和方法稱為倒序相加法［7］. 倒序相加法的本質就是分組配對，轉化成相同數的和來處理.

前面學過等差數列的通項公式為a=a+n（n-1）d，如果用此公式替換④式中的a，將得到什么樣的結果呢？

生7：S==，化簡得S=na+. 所以等差數列｛an｝的前n項和公式為

設計意圖 通過引入高斯定理，以及畢達哥拉斯學派的三角形數，使學生對等差數列的前n項和的由來有一定認識. 通過使用數學語言來表達本節課所學習的知識，讓學生在情境中抽象出數學概念，積累從具體到抽象的活動經驗，從而提高學生的數學抽象、邏輯推理、數學運算等核心素養.

3. 公式應用，加深理解

例1 根據下列各題中的條件，求相應的等差數列｛a｝的前n項和S.

（1）a=-4，a=-18，n=18;

（2）a=14.5，d=0.7，a=32.

設計意圖 使用課本上的練習題，引導學生更加理解等差數列的前n項和公式，為接下來解決“良馬和駑馬”問題做鋪墊，從而發展學生遷移知識的能力.

例2 《九章算術》的盈不足章節中有這樣一題：今有良馬與駑馬發長安至齊，齊去長安三千里，良馬初日行一百九十三里，日增一十三里；駑馬初日行九十七里，日減半里. 良馬先至齊，復還迎駑馬. 問幾何日相逢及各行幾何？

教師將例2轉化為等差數列的前n項和問題：

良馬的：=；

駑馬的：=.

當它們的和為6000時就得到我們想要的結果.

學生求解：+=6000，化簡得12n2+567.5n=12000.

待學生計算后，教師給出答案：約等于15.69.

師：這是我們用數列求和的一般方法求解的，接下來一起看我國古代數學家楊輝在解決“良馬和駑馬”問題時使用的“盈不足術”：先假設兩馬在第十五日相逢，再通過構造幾何圖形來求良馬和駑馬在十五天內走過的路程. 我們將特殊情況推廣到一般情況：在良馬的情形中，用今天的數學語言來表達就是求首項為a（a>0），公差為d（d>0）的等差數列的前n項和，可構造長分別為a，a+d，a+2d，…，a+（n-1）d，寬均為1的n個長方形，則所得到的“階梯形”的面積之和就是所求的等差數列的前n項和，如圖9所示.

師：請同學們看一看，計算“階梯形”的面積之和，直接相加小長方形的面積過于煩瑣，那么怎樣計算更簡便呢？請同學們小組討論.

第一小組：可以將它補充為一個梯形，求梯形的面積，再將多余的部分減掉. 如圖10所示，多余的部分就是陰影部分. 梯形的上底為a，下底為a+（a+nd），高為n，則梯形的面積為n［a+（a+nd）］，再減掉多余的n個小三角形的面積之和，得到S=n［a+（a+nd）］-nd，最后化簡得S=na+n（n-1）d.

第二小組：將其補成一個長方形，如圖11所示，并將其分為兩個部分來求和. 第一部分由n個面積為a的小長方形組成，其面積之和為na；第二部分是邊長為（n-1）d和n的長方形，其面積為n（n-1）d. 因此，等差數列的前n項和為第一部分的面積與第二部分面積的一半的和，即S=na+n（n-1）d.

第三小組：本小組使用的是倒序相加法. 如圖12所示，在“階梯形”右邊加上一個倒置的相同圖形，拼成一個長為a+a，寬為n的長方形. 將這個長方形的面積算出來，取其一半，也就是我們所要求的等差數列的前n項和，得到S=na+n（n-1）d.

師：第一小組將“階梯形”補成一個完整的梯形，第二小組和第三小組則都是將“階梯形”補成一個完整的長方形，其中第三小組使用的是倒序相加法.用這三種方法最終都得到了等差數列的前n項和.

設計意圖 使用“良馬和駑馬”問題讓學生知道數學源于生活，數學方法可以用來解決實際問題. 利用“階梯形”將枯燥、繁雜的文字直觀地展示出來，能促進學生的數形結合思想發展；使用小組討論的方式探究“階梯形”，可增強學生的團隊合作能力，讓學生充分理解運算對象，掌握運算法則，獲取運算思路，求得運算結果，提高學生的數學運算、邏輯推理等核心素養.

4. 布置作業，提升能力

【必做題】

題1：根據下列各題的條件，求相應等差數列｛a｝的有關未知數.

（1）a=20，a=54，S=999，求d及n；

（2）d=，n=37，S=629，求a及a；

（3）a=，d=-，S=-5，求n及a；

（4）d=2，n=15，a=-10，求a及S.

題2：請根據下列條件計算.

（1）今有女子不善織，日減功遲. 初日織五尺，末日織一尺，今三十日織訖. 問織幾何？

（2）今有女善織，日益功疾. 初日織五尺，今一月日織九匹三丈. 問日益幾何？

注釋：“日減功遲”指每日減少的量相同. “訖”指結束.“織幾何”指織了多少尺.

【選做題】

我們在課堂上用“階梯形”求得了遞增等差數列的求和公式，那么你會使用“階梯形”求得遞減等差數列的求和公式嗎？

設計意圖 必做題中求未知數的題目意在使學生更進一步地掌握等差數列的求和公式，發展學生的順向思維和逆向思維；應用題借鑒歷史中的數學問題，意在讓學生知道數列在生活中的存在和使用，幫助學生理解等差數列前n項和公式的運用，從而培養學生的邏輯思維能力；選做題意在使學生嘗試做屬于自己的“階梯形”，從而提高學生的數學建模等能力.

結語

數學史告訴我們，任何屬性的概念、公式、定理、思想等都不是從天上掉下來的，都有其自然發生和發展的過程. 將數學史融入數學課堂，使學生對數學知識既能“知其然”，又能“知其所以然”；既能知其“今生”，又能知其“前世”；既能“近觀樹木”，又能“遠眺森林”［8］. 本節課通過“高斯問題”引入課題，將特殊問題轉化為一般問題，先使用圖形表示等差數列的前n項和，再從代數的角度證明公式，進而培養學生的邏輯推理、數學抽象、數學運算和直觀想象等數學核心素養. 在教學過程中融入數學史，如畢達哥拉斯學派的三角形數、楊輝的“盈不足術”等，構建“知識之諧”. 通過小組討論，學生從中體會到數學知識的來源，營造“探究之樂”. 讓學生感受數學源于生活，與公式“零距離”接觸，使學生成為課堂真正的主人. 使用多種方法探究等差數列的前n項和公式，彰顯“方法之美”， 給學生搭建一座貫穿古今數學文化的橋梁，感受數學文化帶來的巨大吸引力，引發“情感之悅”. 數學史的有效滲透，展示數學家們探究數學孜孜不倦的精神，達成“德育之效”“能力之助”.

參考文獻：

［1］ 中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［S］. 北京：人民教育出版社，2020.

［2］ 余慶純. HPM微課融入高中數學教學的行動研究［D］. 五邑大學，2018.

［3］ 洪燕君. HPM教學實踐驅動下初中數學教師專業發展研究：MKT的視角［D］. 華東師范大學，2017.

［4］ 王蓉. 基于HPM理論的課堂教學實踐與思考——以《等差數列的前n項和》教學為例［J］. 數學教學通訊，2016（33）：9-12.

［5］ 曹純. 九章算術譯注［M］. 上海：上海三聯書店，2015.

［6］ 汪曉勤，陳君煜. HPM視角下數列教學中的直觀想象素養初探［J］. 中小學數學（高中版），2019（04）：57-60.

［7］ 相陽. 例析倒序相加法的應用［J］. 語數外學習（高中版中旬），2020（12）：39.

［8］ 汪曉勤. 數學史與高中數學教學［M］. 上海：華東師范大學出版社，2020.