何時有最大照射寬度
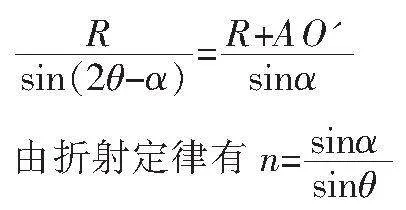

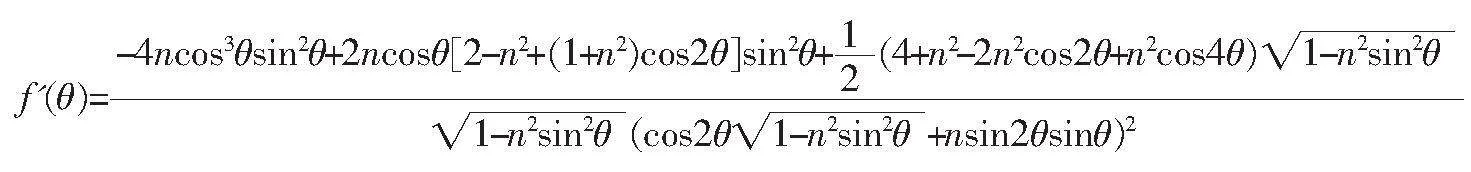
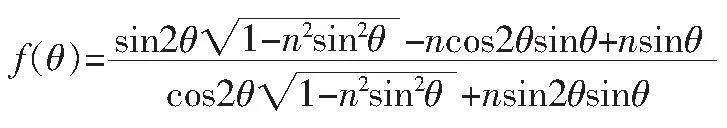



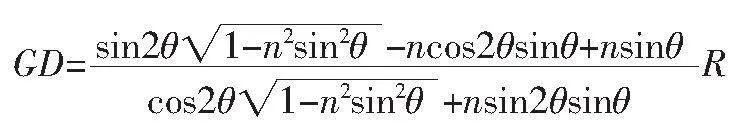

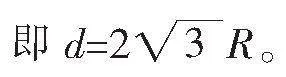


摘 要:通過對一道常見的幾何光學題目進行深入分析,指出現有參考答案中的不當之處,并利用數值計算得到正確結果。同時,對此題進行深入分析,得到一般情況下結果的變化趨勢,論證該題目命制的“痛點”,提出修改建議。最后,分析了近三年高考物理幾何光學試題的命制情況,提出了教學建議。
關鍵詞:幾何光學;折射;全反射
中圖分類號:G633.7 文獻標識碼:A 文章編號:1003-6148(2024)7-0070-3
1 原題呈現
(1)燈柱上有光線出射的圓弧面對應的圓心角φ;
(2)背板上有光線照射的寬度d。
此題現已選編入各種教輔資料,參考答案也基本如出一轍:(1)略;(2)如圖2,根據幾何關系可知,背板上有光線照射的寬度
d=2(HC+GH)=2(EHtan30°+GH)
得
d=2Rcos30°+2(Rsin30°+R)tan30°
2 提出質疑與解答
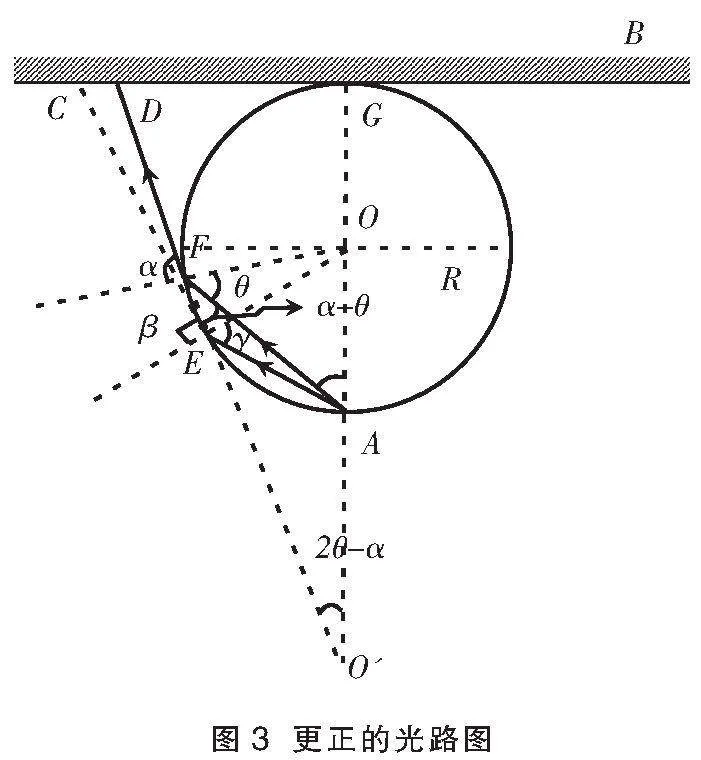
按照參考答案理解,背板上有光線照射的寬度d的最大范圍的臨界位置,即光源發射的入射光線在彩燈壁E點恰好發生全反射時所對應的折射光線CE(該光線實際并不存在)照射在背板上的C點,然后由對稱關系求得光線照射的寬度d。學生從定性分析的角度就很容易提出質疑,為什么光線在背板上的最大偏折就在C點?不少教師可能對此不以為然,不加以證明便告知學生這是顯而易見的。但事實真的如此嗎?現對此題進行深入分析。
對應折射光線為FD,折射角為α。延長DF與GA延長線交于O'點,現對GD的最大值進行討論。
由幾何關系可得
GD=(2R+AO')tan(2θ-α)
在ΔO'OF中,根據正弦定理,有
可得
令
欲求的GD最值,即求解函數f(θ)的最值,
利用Mathematica對f(θ)求導得
3 對此類題目的幾點思考
3.1 對原題的深入分析
通過數值計算,作出不同折射率的透明燈柱全反射臨界角與在背板上有光線照射的最大寬度的臨界光線的入射角之間的關系如圖4所示,其中系列1表示透明燈柱全反射時的臨界角,系列2表示此時背板上有光線照射的最大寬度的臨界光線所對應的入射角。由圖4可知,隨著透明燈柱折射率增大,在背板上有光線照射的最大寬度的臨界光線的入射角始終小于臨界角,二者之間的差值隨著折射率的增大逐漸減小。
最大寬度的臨界光線的入射角之間的關系
故而,對于此題而言,即使改變燈柱折射率,背板上有光線照射的寬度d依然難以求解。另外,生活中常見玻璃材料的折射率介于1.40~2.00。因此,在命制此類題目時應尤其注意結合實際,并注意推理論證過程,避免出現科學性錯誤。
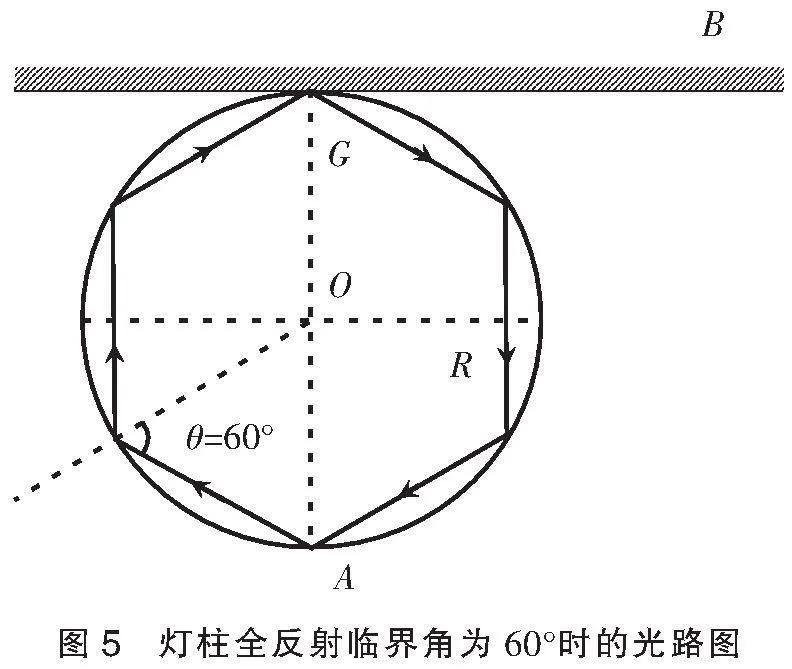
在此,對于模擬試題,第(2)問可進行如下改編:在如俯視圖所示圓平面內,從A點發出的光線經多次全反射回到A點的時間最短。對于此問,需要學生進行推理論證:何時從A點發出的光線經多次全反射回到A點的時間最短?回到A點時間最短即光程最短,也就是發生的全反射次數最少。由題意知,燈柱全反射臨界角為60°,光路圖如圖5所示,便能順利解決。
3.2 高考幾何光學題目命制情況與教學建議
3.2.1 高考幾何光學考題命制情況
通過對近三年全國部分地區高考物理幾何光學題目進行統計與分析發現,關于幾何光學考題的具體試題內容情境主要有:僅含折射光路的試題,僅含臨界光路的試題,含折射、反射光路的試題以及含兩條獨立光路的問題等。問題設計主要包括:折射率計算、光傳播時間計算、邊長度與角度計算等。對于必備知識而言,主要考查光的折射定律、折射率以及全反射。對于關鍵能力而言,主要考查理解能力與推理論證能力。對于學科素養而言,主要考查物理觀念與科學思維。試題主要通過學習探索問題情境體現基礎性、綜合性與應用性的考查要求。
在處理幾何光學問題時,不少學生會反映能算出最終答案,但不知道如何書寫過程。這種情況反映出學生的科學思維有待提高。《普通高中物理課程標準(2017年版)》中明確指出,“科學思維”包括模型建構、科學推理、科學論證、質疑創新等要素[1]。學生不會寫過程,就是不會科學推理與論證,折射出關鍵能力中推理論證能力的不足。造成這種情況的原因有多種,其中值得注意的是,教師在平時教學中就應有意識地引導學生進行科學推理與論證。
通過上述分析可知,前文改編后的題目也較好地符合了高考的考查要求。
3.2.2 幾何光學教學建議
對于高中階段的幾何光學考題,不少教師和學生均認為此類題目很簡單,各種教輔資料也總結出多種處理此類問題的方法,按圖索驥,學生也能拿到分數。但縱觀近年來高考幾何光學問題,不難發現,考題充分體現對學生科學思維的考查,反映學生的推理論證能力。在學生“拿分”與“學科素養”培養之間,作為教師應毫不猶豫地選擇并堅持后者。在此,提出兩點教學建議供參考。
第一,重視必備知識。必備知識的積累是形成關鍵能力與學科素養的基礎。對于幾何光學部分,不能認為學生初中已經學習相關知識就輕視必備知識的學習。不同的學習階段對知識有不同的理解要求。在高中階段,學生對知識的理解不應該依然停留在初中階段的要求。
第二,強化關鍵能力培養與訓練。高考評價體系確立了三個方面的關鍵能力群[2]:以認識世界為核心的知識獲取能力群(理解能力)、以解決實際問題為核心的實踐操作能力群(實驗探究能力)、涵蓋關鍵思維能力的思維認知能力群(模型建構能力、推理論證能力和創新能力)。對于幾何光學問題,高考著重體現在以認識世界為核心的知識獲取能力群的基礎上,對涵蓋關鍵思維能力的思維認知能力群的考查。學生能力培養并非一蹴而就,作為教師,在教學中必須做好積極示范與引導,應避免此類問題不講評的現象。對于有爭議或有價值的點,即使超出高中階段學生的知識范圍,教師也應做好科學推理與論證。這樣,學生不會書寫過程的情況將大大減少,同時,更是對學生學科素養的有效培養。
4 結 論
在教學中,我們鼓勵學生大膽質疑,作為教師,也應如此。對于大型或權威考試試題,不應盲目信服,要有質疑的精神。但質疑也并非無端猜疑,草木皆兵,在大膽質疑假設的同時,更應該小心求證。故而,教師在教學中就應以培養學生的關鍵能力、發展學生科學思維、全面提高學生學科素養為教學出發點,做好示范,引導學生實踐。唯有這般,學生和教師才都能獲得成長。
參考文獻:
[1]中華人民共和國教育部.普通高中物理課程標準(2017年版)[S].北京:人民教育出版社,2018.
[2]教育部考試中心.中國高考評價體系說明[M].北京:人民教育出版社,2019.

