奇思妙想,極限思想

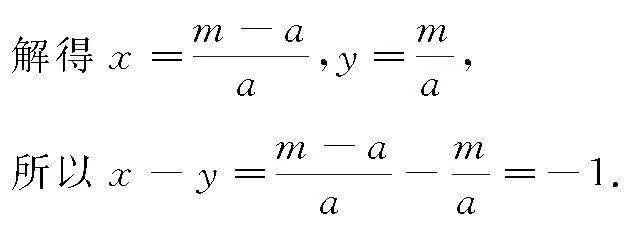

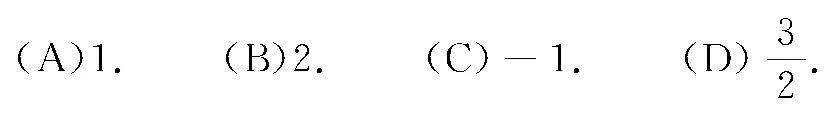
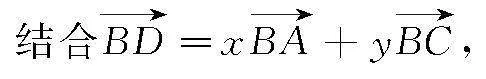
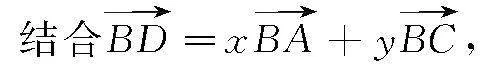

【摘要】抓住一些數學客觀題中的結論特征,合理奇思妙想,結合動點運動規律、圖形變化趨勢以及變量取值限制等場景,從不同思維視角進行極限思想應用,可以更加簡單快捷地處理與解決問題,提高解題效率,提升解題能力,引領并指導數學教學與解題研究.
【關鍵詞】極限思想;高中數學;解題技巧
利用思維的創新性與創造性,奇思妙想,是破解數學問題的一種創新思維.而極限思想是創新思維中的一個重要數學思想,在解決一些客觀題中,巧妙靈活借助極限思想,可以實現抽象到具體、有限到無限、近似到精確、量變到質變等方面的跨越,合理回避多變、復雜的數學運算與抽象、繁雜的邏輯推理等,獨辟蹊徑,降低試題難度,優化解題過程,起到事半功倍的效果.
1 動點運動規律
在解決平面幾何、平面向量、解三角形、平面解析幾何與立體幾何等相關問題中,經常涉及一些動點的運動規律與變化問題,結合數學客觀題中答案為定值的場景,有時可以借助動點運動規律,結合極限思想來巧妙應用,處理起來讓人眼前一亮.
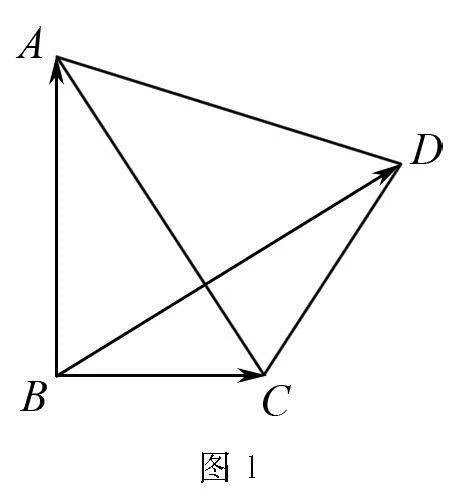
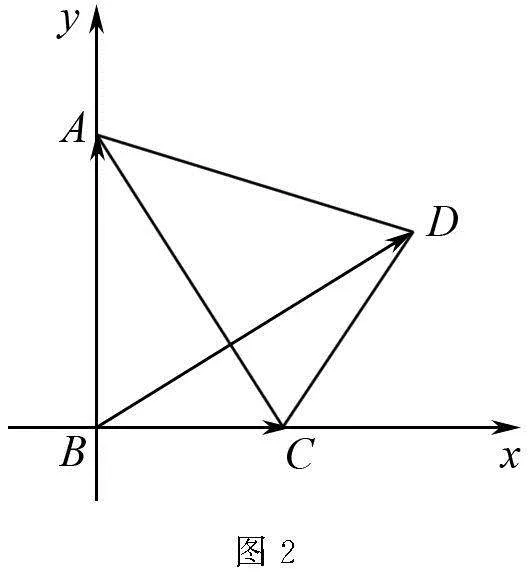
解析 方法1(常規解法) 如圖2所示,以點B為坐標原點,BC,BA所在直線分別為x軸、y軸建立平面直角坐標系,設C(a,0),
由∠DCA=2∠BAC,易知直線CD與直線CA關于直線x=a對稱,
設直線CD的方程為y=k(x-a)(k>0),
則直線CA的方程為y=-k(x-a),
令x=0,可得A(0,ka),
設Dm,k(m-a),
則有m,k(m-a)=x(0,ka)+y(a,0)=(ay,kax),
可得m=ay且k(m-a)=kax,
故填答案:-1.
方法2(極限思想法) 在平面四邊形ABCD中,
∠ABC=90°,∠DCA=2∠BAC,
結合極限思想,讓點D無限接近于點C,
此時x→0,y→1,
結合所求結論中的代數式x-y為定值,
所以x-y=-1.
故填答案:-1.
點評 利用平面向量所對應的幾何圖形中動點的運動規律,以及所求結論中的代數式為定值,經常采用平面向量的基底法、幾何法以及坐標法等常規方法來處理,推理過程比較復雜,數學運算量也較大;而結合題目特點,利用極限思想,讓點“動”起來,結合動點的變化與運動規律,利用點的極限位置分析直觀圖形,更加簡捷有效.
2 圖形變化趨勢
在解決函數圖象、平面幾何、平面解析幾何與立體幾何等相關問題中,經常涉及一些圖形變化趨勢與應用問題,結合數學客觀題中答案為定值的場景,經常可以通過圖形變化趨勢,結合極限思想來巧妙應用,尋找極限狀態下圖形的特征,有時對問題的破解有奇效.
例2 若正四棱錐相鄰側面所成的二面角的平面角為α,側面與底面所成的二面角的平面角為β,則2cosα+cos2β的值是( )
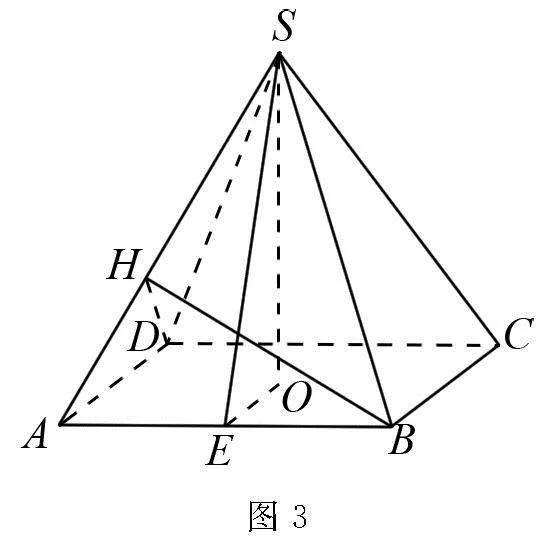
解析 方法1(常規解法) 如圖3所示,設正四棱錐S—ABCD的底面邊長為a,側棱長為b,過點S作SE⊥AB于點E,SO⊥底面ABCD于點O,連接EO,則∠SEO即為側面與底面所成二面角的平面角,即為角β,
過點B作BH⊥SA于點H,連接DH,BD,
由△SAB≌△SAD,所以DH⊥SA,
則∠BHD即為兩個側面所成的二面角的平面角,即為角α,
故選擇答案:(C).
方法2(極限思想法) 由于正四棱錐的圖形是運動變化的,
故選擇答案:(C).
點評 利用空間幾何體的運動變化趨勢以及所求結論中三角函數值為定值這一條件,結合極限思想,通過圖形的運動極限——高無限增大,從而改變常規解法中“畫圖難,邊不定,解難算,費時間”等局面,創新條件,開拓思維,開創“圖不畫,邊不求,角不算,贏時間”新局面.
3 結語
極限思想是探索解題新思路,探究解題新模式的一種奇思妙想,給人一種“撥開云霧見晴天”的獨特視角.對于解決一些數學客觀題中,巧妙融入極限思想,以“動態”制約“靜態”,以“變量”約束“常量”,避免復雜運算,回避繁雜推理,化繁為易,實現巧妙、快捷、正確解答問題,全面拓展數學思維,提升數學能力,培養數學核心素養.

