化歸思想在高中數學解題中的運用

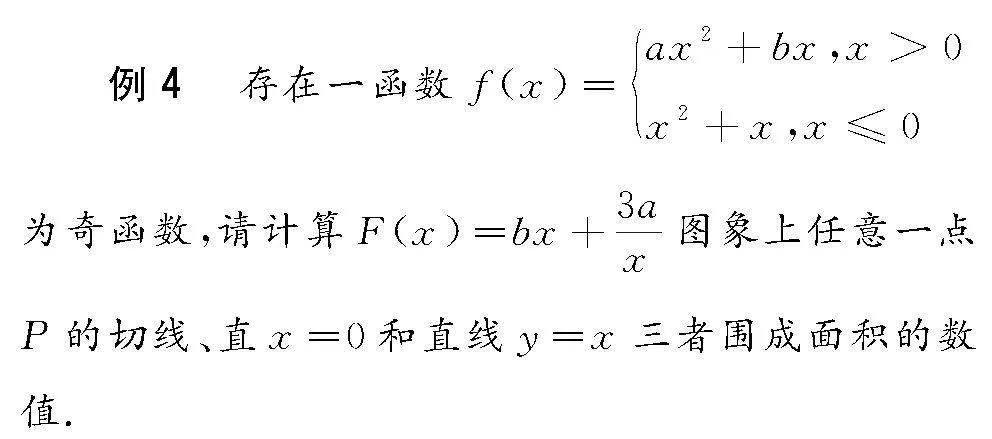
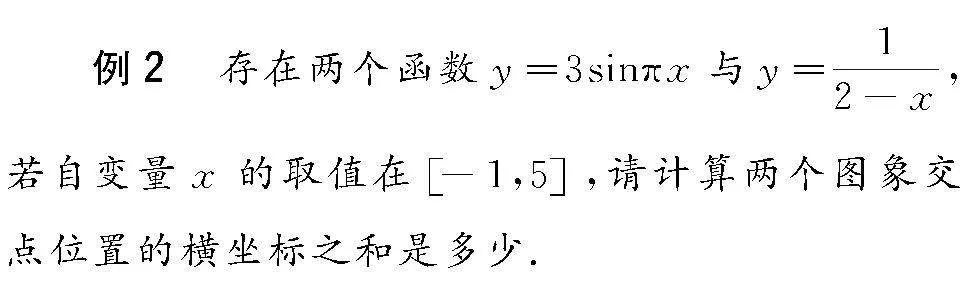
【摘要】化歸思想是高中學生解答數學題目時常用的一種解題思想.基于化歸思想，學生能夠將已知信息等價轉變為另一種信息.通過使用化歸思想解答高中數學問題，能夠幫助學生將繁瑣復雜的問題簡單化，并將未知、不熟悉的內容轉變為學生熟悉的數學知識，最終提高學生的解題質量.研究發現，學生使用化歸思想能夠提高對數學知識的實踐運用能力，不斷完善數學思維.

【關鍵詞】化歸思想;解題技巧;高中數學

利用化歸思想能夠降低學生解答數學問題的難度，幫助學生理清繁瑣的已知信息，進而將復雜的問題條理化、簡單化[1-3].因此，高中數學教師需要在日常教學中著重提高學生對化歸思想的運用能力，通過典型例題強化學生的這方面技能，進而培養學生形成良好的數學核心素養.

1 利用靜態與動態的關系化歸

利用靜動態關系解題是化歸思想中一種常見的解題策略，通過運用在函數類型的數學問題中，學生可以根據函數間的變量關系進一步解答.

2 利用形與數間的關系化歸

根據形與數間的關系進行解題也是化歸思想的常見解題策略，學生在該環節中需要巧妙轉化幾何圖形與代數式間的關聯，進而將抽象的已知條件形象化、直觀化，進而提升解題效率[4-5].

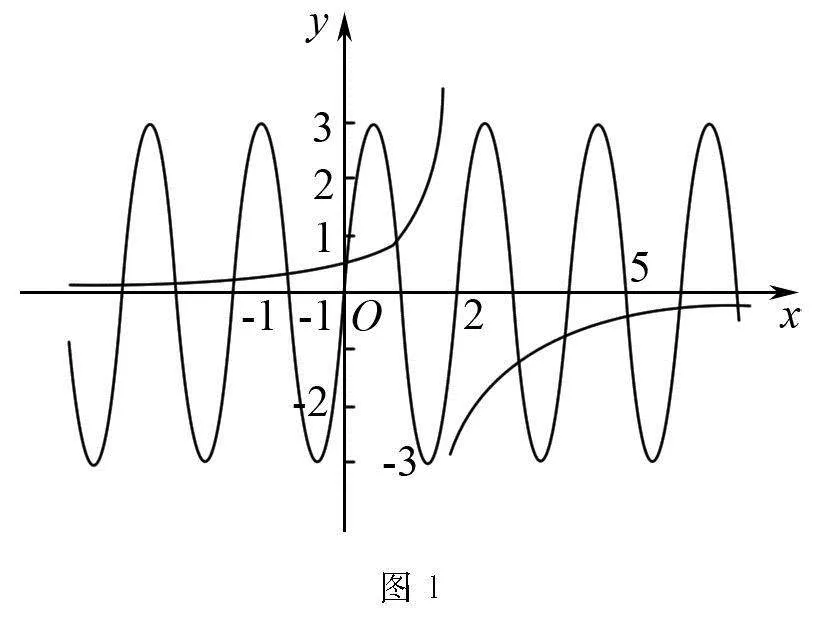
解析 例題2屬于十分典型的探究兩個函數在某一區間交點的數學問題，很多學生在拿到題目后感到無從下手，教師需要引導學生轉換解題方向，靈活運用數形關系進行化歸.如在坐標系中繪制出兩個函數的圖象，具體如圖1所示，帶領學生仔細觀察兩個函數在-1，5的圖象信息，學生能夠發現兩者在-1，5共有4個交點，并處于2，0的兩邊，呈兩兩對稱，由此看出2，0為兩組交點的中點，根據所學的中點坐標公式就能夠快速求解出正確答案，即：8.

3 利用整體與部分間的關系化歸

在解答立體幾何類數學問題時，學生能需要助整體與部分間的關聯進行化歸思考，尤其在面對翻折、對稱等數學問題時，教師需要指導學生將復雜的立體幾何信息轉變為較為簡單的向量問題，進而解出答案.

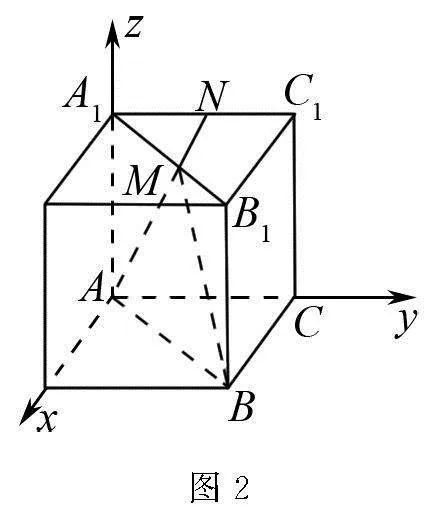
例3 在直三棱柱ABC－A1B1C1中，已知∠BCA為直角，且M為線段A1B1的中點，N則為線段A1C1的中點，此外BC=CA=CC1，請大家計算BM和AN間夾角的余弦值.

4 利用特殊與一般間的關系化歸

在面對某些數學問題時，學生可以利用特殊與一般間的關系進行化歸，根據特殊值或特殊情況來快速解出答案，這就要求學生掌握特殊與一般間的轉化方式，快速找出問題中存在的特殊情況.

5 結語

通過上述的分析可以發現，高中數學教師需要在日常教學中著重提高學生的數學綜合能力，幫助學生完善數學核心素養.化歸思想作為數學解題中常用的、高效的解題方式，教師應當通過不同類型的數學題目來提高學生對化歸思想的理解與運用能力.

參考文獻：

[1]王開江.高中數學解題教學中邏輯思維的培養——以數列解題教學為例[J].數理化解題研究，2023（27）：8-10.

[2]張平.高中數學教學中化歸思想的有效應用[J].中學數學，2023（15）：64-65.

[3]郭啟航.高中數學資優生化歸能力的調查研究[D].上海：華東師范大學，2023.

[4]楊興剛.化歸思維下數學微專題教學初探 [J].中學數學研究（華南師范大學版），2023（12）：28-30.

[5]祝均林.轉化與化歸思想在高中數學教學中的應用[J].數學之友，2023，37（12）：15-17.