關(guān)于空間幾何體積考查重點的探究舉例

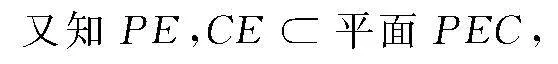
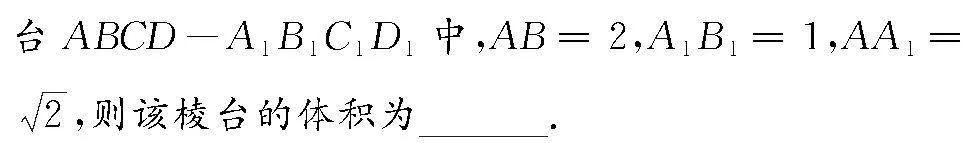
【摘要】體積問題是高中數(shù)學中的典型題目，問題構(gòu)建形式多樣，考查側(cè)重點存在差異.具體求解時應(yīng)先明晰問題、條件，把握幾何體特征，再結(jié)合相關(guān)知識確定解法.本文結(jié)合2023年高考真題開展幾何體積問題探究.

【關(guān)鍵詞】空間幾何；體積；解題技巧

高考注重對空間幾何體積的考查，問題類型較為多樣，實際考查的重點也有一定的差異，涉及到兩方面：一是思維能力的考查，如學生空間幾何觀；二是知識方法考查，如常規(guī)體積公式，體積模型構(gòu)建等.下面結(jié)合2023年高考真題開展體積問題考查探究.

考查形式1 分割構(gòu)建求體積

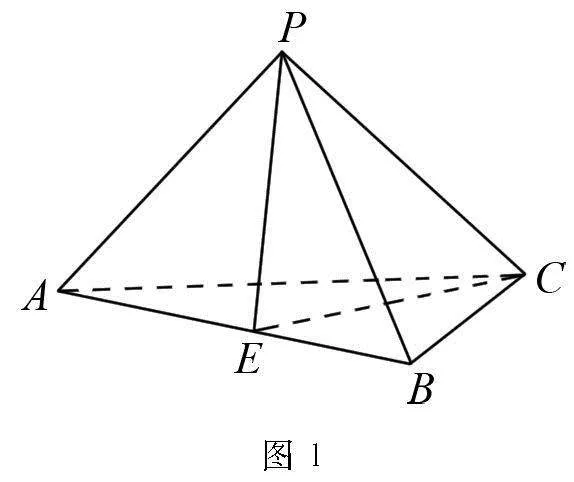
分析 本題目求解三棱錐的體積，分析證明幾何體的高是關(guān)鍵，后續(xù)求解三棱錐的體積可以采用分割體積法.

解 取AB的中點E，連接PE，CE，如圖1所示.

因為△ABC是邊長為2的等邊三角形，

PA=PB=2，

所以△PAB是等邊三角形，

所以PE⊥AB，CE⊥AB，

PE∩CE=E，

所以AB⊥平面PEC.

綜上可知，答案為（A）.

小結(jié) 上述求解三棱錐的體積時采用了分割體積的方法，即構(gòu)建V=VB－PEC+VA－PEC的體積模型.后續(xù)再通過空間位置關(guān)系分析確定幾何體的底和高.使用分割體積法求解體積問題時，需要注意兩點：一是盡量分割為規(guī)則的幾何體，充分利用線面垂直、面面垂直關(guān)系；二是準確分割，確保不重疊、不疏漏.

考查形式2 比值轉(zhuǎn)化求體積比

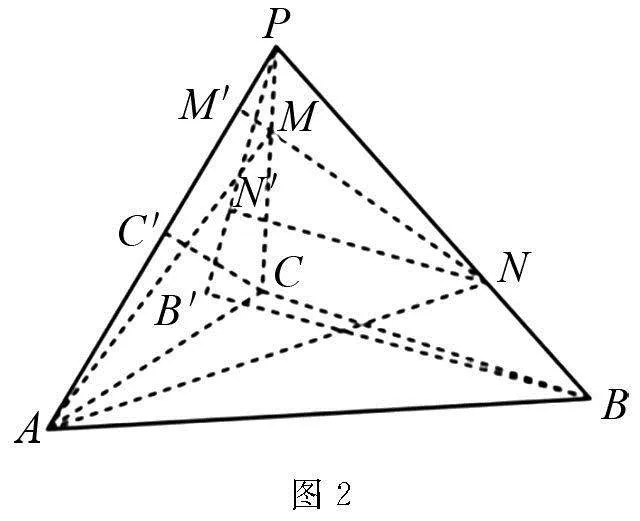
分析 本題目求解三棱錐P－AMN和三棱錐P－ABC的體積之比，屬于體積比值問題，基本思路是構(gòu)建體積模型，再通過比值轉(zhuǎn)化來求解幾何體積的比.構(gòu)建體積模型時需要注意對空間位置關(guān)系進行分析，確定三棱錐的底和高.

解 如圖2所示，分別過點M，C作MM′⊥PA，CC′⊥PA，設(shè)垂足分別為M′，C′.

過點B作BB′⊥平面PAC，垂足為B′，連接PB′，

過點N作NN′⊥PB′，垂足為N′.

因為BB′⊥平面PAC，

綜上可知，答案為（B）.

小結(jié) 上述求解兩個三棱錐的體積之比，屬于體積比值問題，具體求解時分為兩個階段：階段1，分別構(gòu)建三棱錐的體積模型，將問題轉(zhuǎn)化為線段比值問題；階段2，結(jié)合空間幾何中的位置關(guān)系，提取兩線平行，求解線段比值.

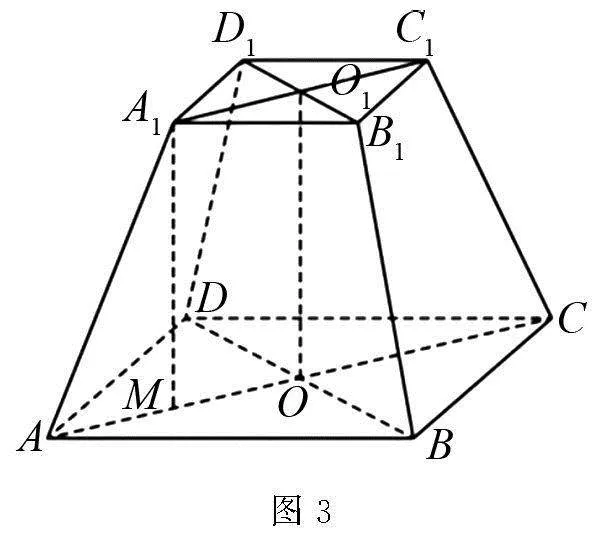
考查形式3 巧用公式求棱臺

例3 （2023年新高考I卷理數(shù)第14題）正四棱

分析 求棱臺的體積，可直接調(diào)用體積公式.求解時可結(jié)合圖象，依次求得A1O1，AO，A1M，再代入體積公式即可.

解 如圖3所示，過A1作A1M⊥AC，垂足為M，

易知A1M為四棱臺ABCD－A1B1C1D1的高.

結(jié)語

總之，空間幾何體積題型多樣，往往融合了空間關(guān)系，考查體積公式及模型構(gòu)建.上述是其中常見的三種形式，涉及了體積分割法、體積比值的常見轉(zhuǎn)化思路，以及特殊棱臺的體積公式.探究學習中需注重總結(jié)公式定理，深刻理解空間關(guān)系的分析方法，靈活運用體積模型構(gòu)建的技巧.