高中數學解題中函數思想的運用策略

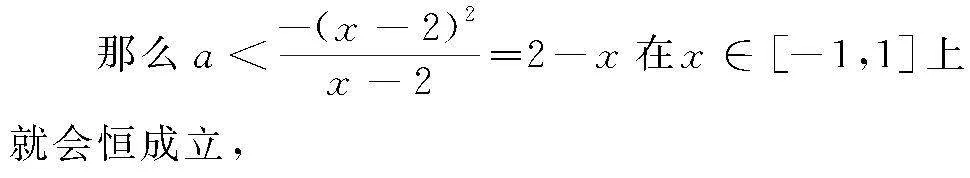
【摘要】在高中數學教學中函數模塊占據著重要的地位，其能夠基本貫穿整個數學知識體系.此外，函數思想也是一種十分常見的數學思想，學生能夠運用該思想快速解答數學問題.因此，教師在開展解題教學時，需要為學生詳細講解函數思想的內涵，并通過典型例題培養學生掌握相應的解題技能.

【關鍵詞】高中數學；解題教學；函數思想

函數思想是一種高中學生解答數學問題的常用解題策略.要想熟練運用函數思想解答數學題目，高中學生就需要了解函數思想的內涵[1].實際上，學生在深度學習中能夠發現，函數思想主要是運用了變量與定量間存在的關系，運用一個事物隨著另一個事物的改變而產生變化的規律.因此，高中數學教師在開展解題教學時，就需要引導學生將已知條件轉變為數學語言，并據此建立相應的函數關系，進而找出正確答案.

1 利用函數思想解答集合類的數學問題

集合模塊的知識是整個高中數學體系中較為基礎的內容，其是學生在高中階段最初學習的知識要點[2].當使用函數思想來解析集合類數學問題時，授課教師首先需要引導學生探究函數與集合間可能存在的關系.實際上，我們能夠將函數轉變為2個集合的映射，即包含函數值與自變量兩個集合.

解析 閱讀題干信息可以發現，其向我們表明了2個集合存在的關聯，集合中還包含了不等式的內容，如果學生采用常規思維進行思考，則解題過程十分復雜、繁瑣，很容易在解題中出現錯誤.因此，授課教師可以引導學生借助函數思想來分析函數值與自變量之間的關系，進而明晰解題流程.

以下為具體解題過程：

把集合A簡化處理后能夠列出：

A=xx>1且x<3.

假設f（x）=x2－2x+m，

g（x）=x2－2nx+5，

那么B1=xx2－2x+m≤0，

B2=xx2－2nx+5≤0，

B=B1∩B2，

因此能夠推出f（1）≤0，f（3）≤0，

且g（1）≤0，g（3）≤0.

將對應數值代入題干中的不同式子后就可發現m與n的取值范圍，從而大大降低解題難度.

2 利用函數思想解答不等式類的數學問題

函數模塊知識與不等式模塊知識看似不相關，實+EqFE6bDYPqEgcG7ThSfKg==際上在高中數學解題過程中卻存在密切聯系，數學教材中還有“不等式與二次函數”的教學內容，這也是為了幫助學生利用函數思想解決不等式問題作鋪墊[3-4].學生在探究中需要運用不等式的性質而推斷函數單調性的特征，進而快速解答恒成立與最值問題.

例2 假設對任意x∈［－1，1］，均保證f（x）=x2+（a－4）x+4－2a數值大于0恒成立，那么請大家推斷a的取值范圍.

解析 在拿到這一題目后很多學生感到難度較大，不好下手，教師就可鼓勵學生直接借助函數思想來探究，并將原本的題干信息轉變為：在一閉區間內存在某一個含參數的二次函數始終大于0的問題，整合后得出a的取值范圍，即：a<1.

以下為具體解題過程：

對于任意x∈［－1，1］，f（x）=x2+（a－4）x+4－2a上的數值都會比0大，

因此x2+（a－4）x+4－2a>0，

得出a（x－2）>－x2+4x－4，

由于x∈［－1，1］，

所以a<（2－x）min，

那么當x=1時，（2－x）min=1，由此得出a<1.

在拿到題目后學生需要有效借助函數思想來探究，整個解題環節中學生不需要分析Δ<0的情況，這不僅能夠保障所有情況不被遺漏，更能夠提高學生的解題正確率，讓學生快速得出正確答案.

3 利用函數思想解答數列類的數學問題

數列模塊的知識屬于高中數學體系中的一大核心內容，也是高考中的必考知識點.因此，學生不mkOrasai8/Xz1ImHTnUg8w==僅需要掌握數列的概念和內涵，還需要了解如何運用等差、等比數列的相關知識解答數學問題[5].實際上，數列能夠歸為函數的延伸產物，如果一個函數的定義域是正整數集，那么就能夠將這一函數看作數列.在數列習題訓練時，尤其針對求解最值的數列問題，授課教師可以引導學生運用函數思想來解答，從而減少解題流程，快速得出正確答案.

解析 若高中學生純粹根據數列的相關知識進行求解，雖然能夠計算出正確答案，但解題過程較為繁瑣復雜，更容易在求解中出現錯誤，最終影響正確率.因此，數學教師可以鼓勵學生使用函數思想進行探究，試圖從題干信息中找出變量，并明晰量與量之間的函數關系，進而得出答案.

以下為具體解題過程：

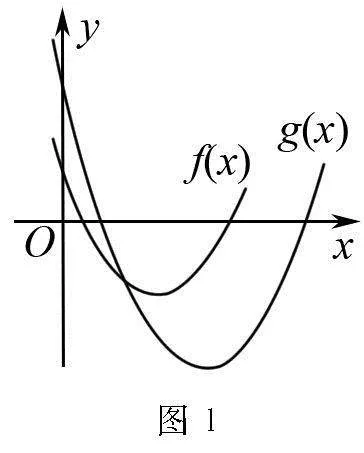
閱讀題干后能夠得出f（x）=3x2+1，g（x）=5x，

由此推斷bn=6a2n－5an+1，n∈N*，

將相關數值代入后可以得出：

4 結語

綜上所述，在高中數學教學中，隨著課堂知識深度與難度的逐步提升，導致數學問題的解題難度也逐漸攀升，授課教師需要傳授學生便捷、有效的解題技能，從而幫助學生快速找出問題的答案.利用函數思想能夠將很多常見的數學問題轉變為函數問題，讓學生突破傳統解題模式的障礙，快速找出關鍵點，最終將復雜的題目直觀化、簡單化.

參考文獻：

[1]譚雪妗.函數與方程思想破解高中數學教學難點探析[J].數理化解題研究，2023（18）：2-4.

[2]朱坤密.基于函數思想的高中數學解題探究[J].數學學習與研究，2023（18）：108-110.

[3]馬艷波.新課程背景下高中數學變式題設計方法探析——以“數形結合思想在函數問題中的應用”一課教學為例[J].延邊教育學院學報，2022，36（03）：143-145.

[4]杜維達.數學素養視域下利用函數與方程思想破解高中數學教學難點的案例研究[J].讀與寫：（下旬），2022（07）：10-12.

[5]張天濤.運用函數思想解決高中數學問題的研究[J].中華活頁文選（高中版），2022（05）：112-114.