直線與雙曲線的綜合問題分析與探究

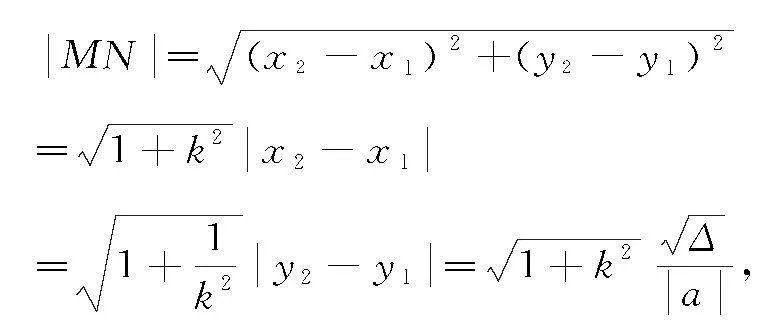
【摘要】直線與圓錐曲線相結合是高中數學的重難點知識，其中以直線與雙曲線的相交為背景，求雙曲線方程、直線方程、直線與雙曲線相交弦長等綜合問題常在高考的填空題和解答題中出現，題目難度大，運算復雜，充分考查了學生的函數思想和邏輯推理能力.本文對直線與雙曲線的綜合問題進行分析與探究，并列舉了兩道例題進行講解，以期望提高學生解答直線與雙曲線綜合問題的技巧.

【關鍵詞】直線；雙曲線；解答技巧

1 直線與雙曲線的位置關系問題

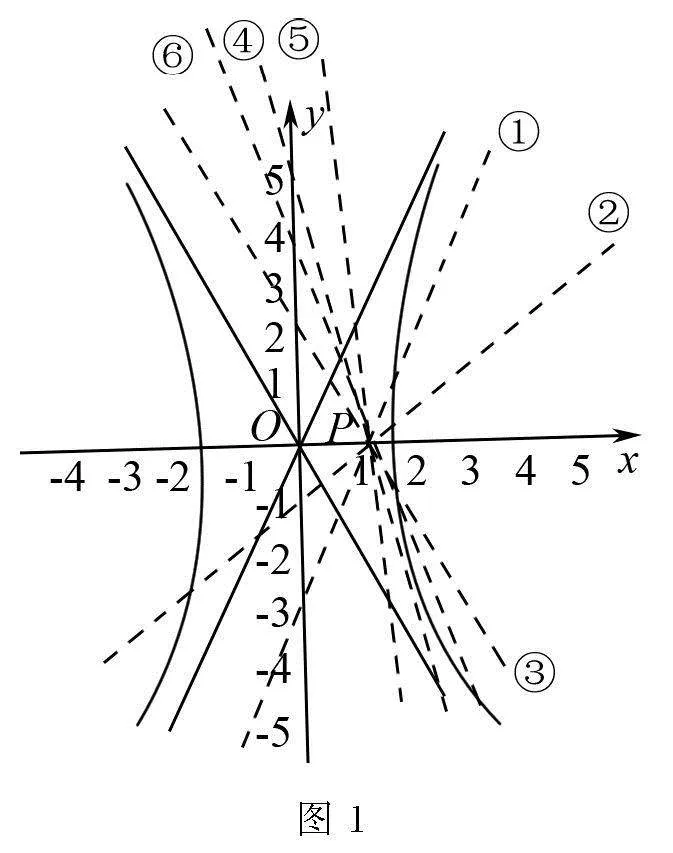
判斷直線與雙曲線的位置關系，有幾何法（漸近線法）可以根據漸近線的斜率判斷直線與雙曲線的位置關系.如圖1所示，設此雙曲線的漸近線斜率為±k，當直線的斜率等于±k時，直線與雙曲線相交于一點，直線①=1③=3均與雙曲線右支交于一點；當直線過點P且斜率在－k，k上時，直線與雙曲線左右兩支各交于一點，如直線②=2；當直線過點P且斜率在－∞，－k∪k，+∞上時，直線可能與雙曲線的右支交于兩點，如直線⑥=6，也可能與雙曲線右支相切，如直線④=4，還可能與雙曲線相離，如直線⑤=5.注意：IFAMnLY8fC7Gu/RcuSjQIzRIE341ZEnfvaSynkP0LeM=當直線與雙曲線只有一個交點時，有兩種可能情況：直線與雙曲線相切；直線與雙曲線的漸近線平行.

2 直線與雙曲線相交的弦長問題

設直線與雙曲線相交于點Mx1，y1，Nx2，y2，則可結合一元二次方程根與系數的關系得到如下弦長公式：

其中k為直線的斜率，a為x2的系數.

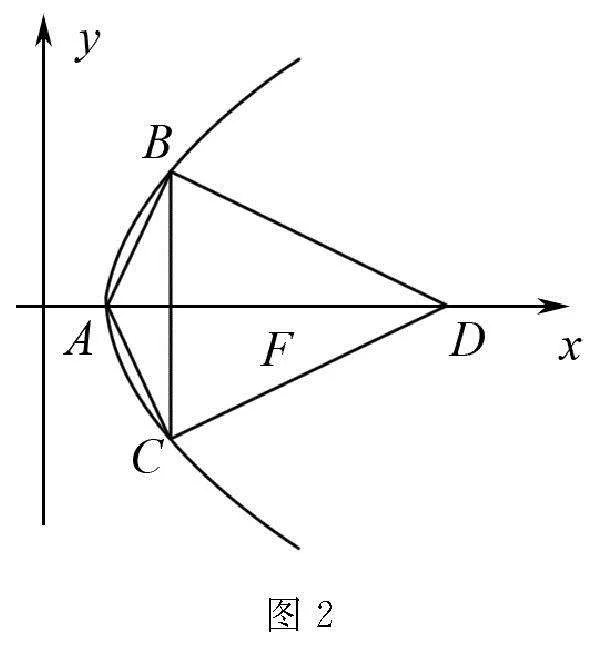
設Ax1，y1，Bx2，y2，

因為F22，0，所以直線l的方程為y=kx－2，

所以k4+8k2－9=0，解得k=±1（另外兩解不成立），所以直線l的方程為y=x－2或y=－x+2.

3 結語

高中數學中，解直線與雙曲線的綜合問題是一個難點問題，解決這類問題需要綜合運用函數、代數、幾何和分析等多種數學思想，通過對直線和雙曲線的性質和方程進行分析和比較，找到它們的交點或者相對位置關系，從而找到解答問題的突破點.

參考文獻：

[1]樂培正.圓錐曲線與圓、向量、直線的綜合[J].新世紀智能，2023（30）：35-36.

[2]姜艷.例談運用代數法判斷直線與雙曲線位置關系的思路[J].語數外學習（高中版下旬），2022（05）：50.

[3]辛蘭萍.立足數學核心素養的高中數學實驗課的教學設計案例——以“雙曲線與直線的位置關系”為例[J].數學學習與研究，2022（11）：68-70.