函數值域的求解策略


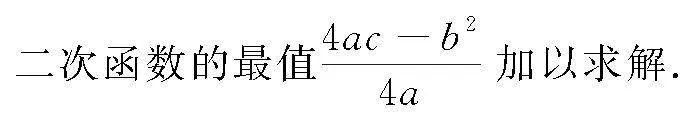

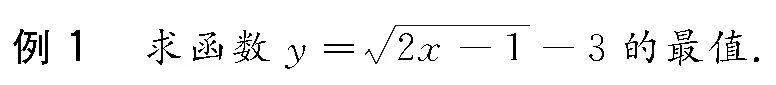

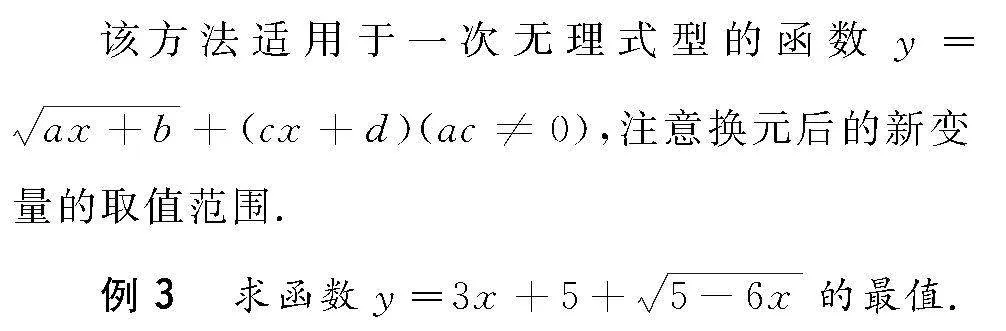
【摘要】函數值域是解決與函數有關問題中的一個重要環節,可單獨命題,也可輔助應用.本文借助實例,就求解函數的值域的主要技巧與方法策略加以剖析,歸納解題方法,總結規律策略,引導教師的數學教學與學生的學習.
【關鍵詞】函數值域;高中數學;解題技巧
函數的值域是函數在定義域內對應的函數值中的取值范圍,其關鍵是確定相應的最大值或最小值.因此,求解函數的值域時要把定義域內對應的一切極值和端點處函數值加以比較.在高考中以求解函數的值域為主要的考點,帶動函數的值域、最值等相關問題的求解.
1 觀察法
該方法適用于自變量x只出現一次的函數,注意結合函數的變化趨勢.
分析 對于一些簡單的函數,可通過定義域及對應法則,用觀察的方法來直觀確定函數的最值問題.
點評 算術平方根具有雙重非負性,即被開方數的非負性、值的非負性,這也是解決此類函數值域的技巧方法.
2 配方法
該方法適用于二次型函數y=af2(x)+f(x)+c(a≠0),注意自變量x的取值范圍及二次函數對應的圖象對函數的最值的影響,有時可直接利用
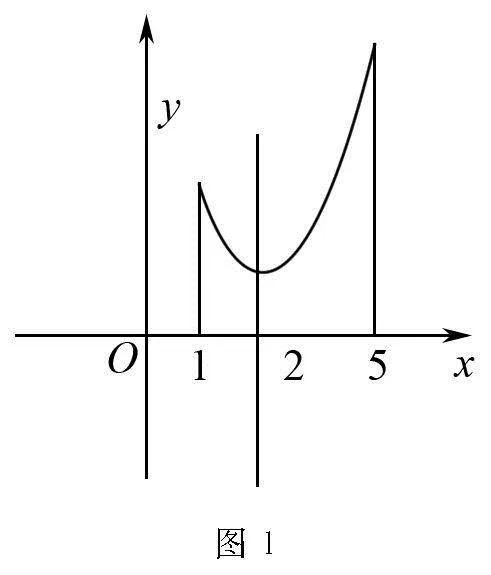
例2 求函數y=x2-4x+6,x∈1,5的值域.
分析 這是求關于二次函數在給定的定義域范圍內的值域問題,可用配方法結合二次函數的圖象求解.
解 將函數配方得:
y=x2-4x+6=(x-2)2+2,
又由于x∈1,5,函數y的對稱軸為x=2,可畫函數的大致圖象,
如圖1所示,易知當x=5時,y=11,
當x=2時,y=2,
所以函數y的值域為2,11.
3 換元法
分析 此題的函數由于含有根號,不便于求最值,可采用換元法去掉根號,轉化成二次函數再求對應的最值問題.
4 幾何法(數形結合法、圖象法)
該方法適用于較容易與幾何圖形聯系的函數,以圖形與圖形之間的位置關系和直線的斜率為主.此題型是函數解析式具有明顯的某種幾何意義,若運用數形結合法,往往會更加簡單,解題過程會一目了然,賞心悅目.
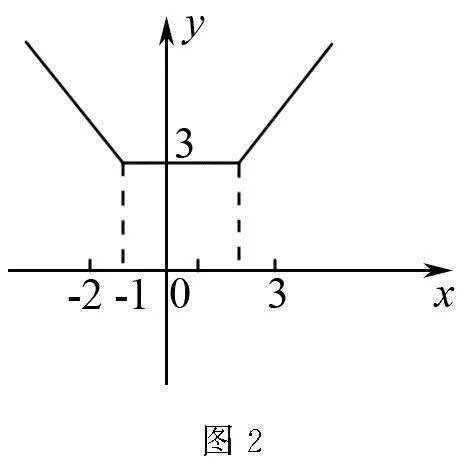
例4 求函數y=|x+1|+|x-2|的值域.
分析 要求函數y的值域,關鍵是求解其最小值,通過去掉絕對值符號,將含絕對值符號的解析式轉化為不含絕對值符號的解析式,畫出圖象,根據圖象判斷其對應的最值.
解 將函數的解析式中的絕對值符號去掉,化成分段函數:
該函數圖象如圖2所示,則根據圖象可知函數y的最小值為3,則其值域為3,+∞.
5 反函數法
分析 將題目用含x的關系式表示的y,轉化為用含y的關系式表示x,結合主元的變換,利用題設中x的取值限制構建不等式,進而通過解不等式確定函數的值域即可.
6 結語
函數的值域問題在高中數學中占有重要地位,應用廣,且知識面寬,綜合性強,解法靈活多變.隨著后繼的不斷深入學習,學生會接觸更多種函數值域的求解方法.在實際求解中,各種方法往往可以相互滲透,有時也可以將多種方法同時運用.

