高中數學不等式的6種解題方法


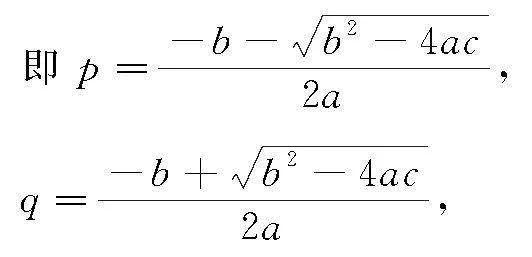

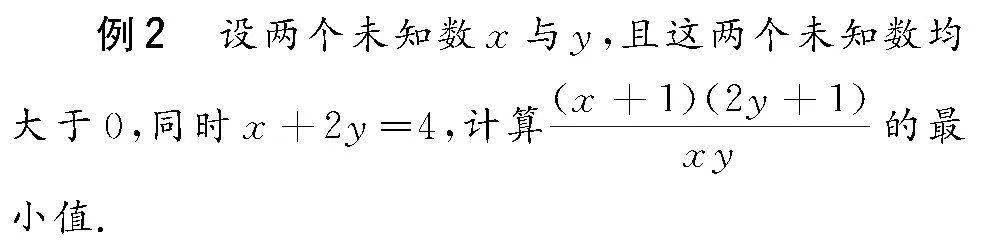

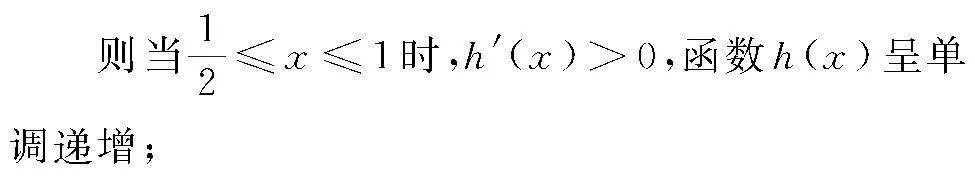
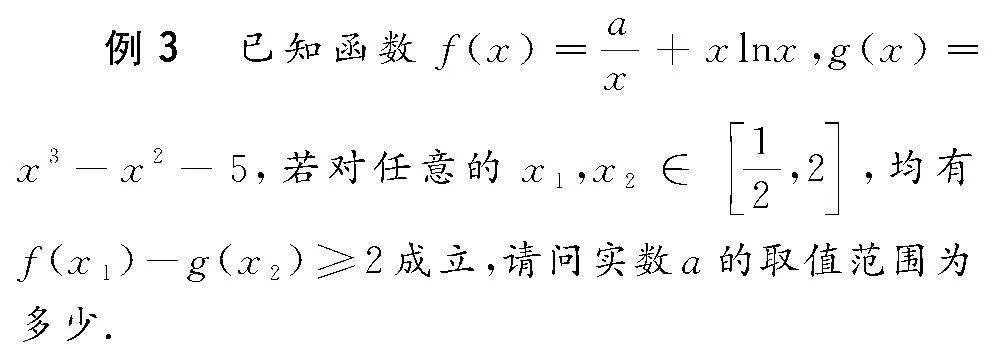
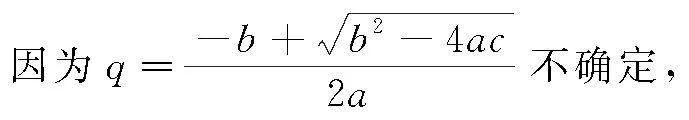

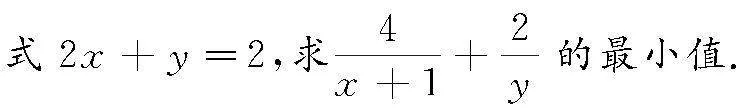
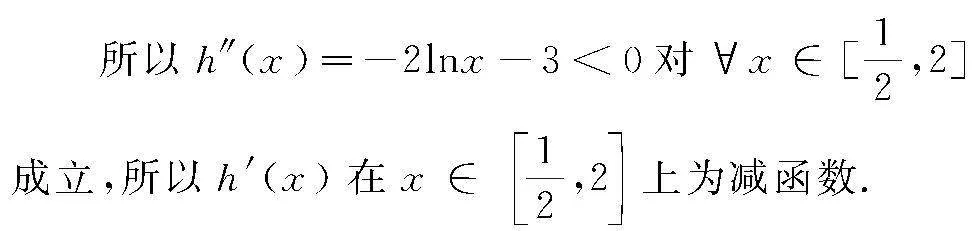
【摘要】不等式是高考數學常見題型,此類題型多變復雜,再加上不同類型不等式問題具有顯著特征,也因此有多種解題方式.教師需指導學生歸納總結題型和解題方式,切實提升解題準確度與效率.
【關鍵詞】高中數學;不等式;解題技巧
1 運用等價轉化解答問題
(A)結論①②均成立.
(B)結論①②均不成立.
(C)結論①成立,結論②不成立.
(D)結論①不成立,結論②成立.
②當a<0且b2-4ac<0時,不等式p:ax2+bx+c<0(a≠0)解集為{x|x<p或x>q},設p,q為方程ax2+bx+c=0兩個不同實數根.
使ax20-bx0+c<0,
則x0<p或x0>q,
所以無法確定c值
所以結論②不成立,選項(B)為正確答案.
2 運用基本定理解答問題
解 已知x+2y=4,
左右各加1即可獲得x+2y+1=5,
拆分(x+1)(2y+1)獲得2xy+x+2y+1,
3 運用構造法解答問題
解 由g(x)=x3-x2-5,
可得g′(x)=3x2-2x,令g′(x)=0,
則h′(x)=1-2xlnx-x,
又因為h′(1)=0,
當1≤x≤2時,h′(x)<0,函數h(x)呈單調遞減.
則h(x)max=h(1)=1,
所以a的取值范圍為1,+∞).
4 運用函數解答問題
例4 已知,函數f(x)在0,+∞上為偶函數,呈單調遞減,若f(2a-1)>f(1),請問實數a的取值范圍.
解 根據題意得知,函數f(x)為偶函數,
所以f(2a-1)>f(1)等價于f(|2a-1|)>f(1).
因為fx在0,+∞呈單調遞減,
|2a-1|≥0,1>0,
所以|2a-1|<1,去絕對值得-1<2a-1<1.
所以0<a<1.
實數a取值范圍為(0,1).
5 運用配湊法解答問題
例5 已知正實數x與y,上述兩個實數滿足等
解 已知2x+y=2,若在式子左右兩邊各添加2,
即可獲得2x+y+2=4,
簡化式子可得2(x+1)+y=4.
6 運用數形結合解答問題
例6 已知,關于x的不等式x2≤4-2x+m,如果至少存在一個x≥0使得該不等式成立,請問m的取值范圍是多少.
解 整理不等式x2≤4-2x+m,
獲得2x+m≤-x2+4.
將其視為兩個函數,y=2x+m與y=-x2+4,
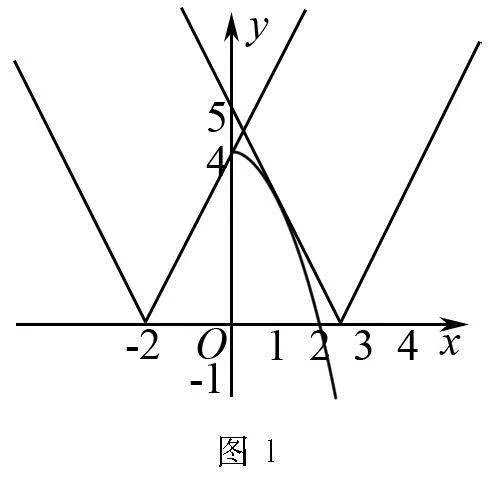
在此過程中需思考問題反面,若對于任意x≥0,均有2x+m>-x2+4如,在同一平面直角坐標系中畫出兩個函數圖象,圖1所示.
觀察圖1可得知,當m的值發生變化時,函數y=2x+m圖象沿x軸運動,圖1為兩個臨界條件,分別對應m>4或m<-5,滿足題意m的取值范圍為-5,4.
參考文獻:
[1]許明貴.高中數學不等式解題的常見方法和解題技巧[J].數理天地(高中版),2023(07):33-34.

