動態的考查，靜態的訓練，動靜轉換以靜制動

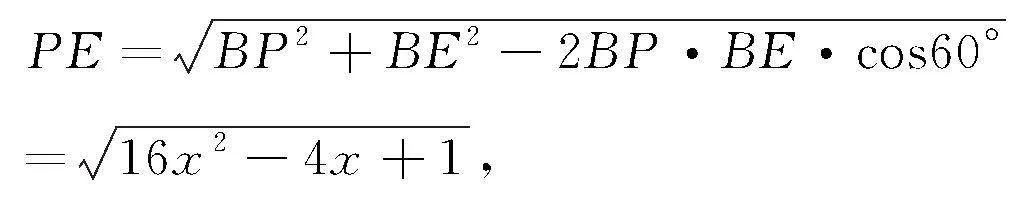
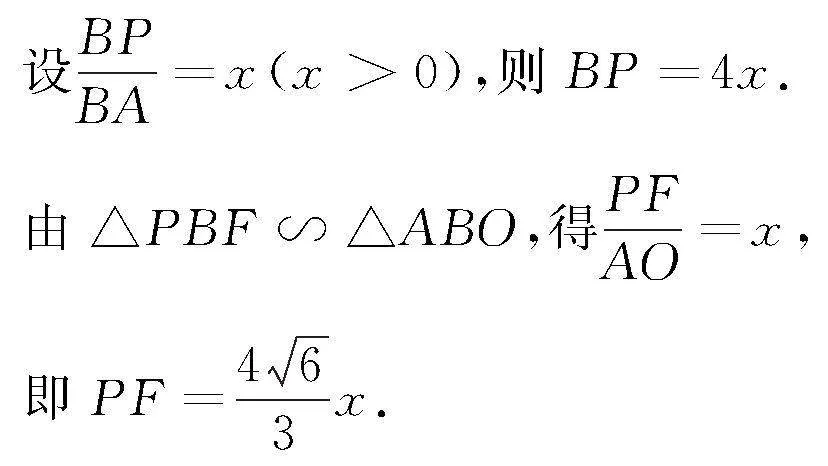
【摘要】對高考題進行靜態設計，分組分任務完成，規范重點知識落實，把各自結果匯總，引領高一高二初學的學生觀察歸納猜想尋覓規律；對高考題進行類題整合訓練，多題歸一，動態的最值問題，靜態化思考，動靜轉換以靜制動，提升認知境界，準確把握算法、算理、算律、規律，掌握解題教學的基本策略技巧．

【關鍵詞】高中數學；法向量；解題技巧

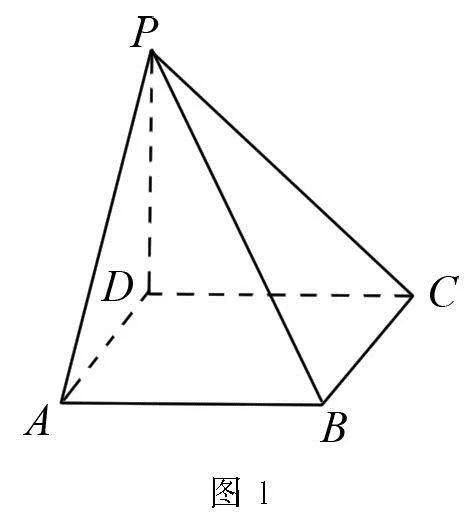
高考原題 如圖1，四棱錐P—ABCD的底面為正方形，PD⊥底面ABCD．設平面PAD與平面PBC的交線為l．

（1）證明：l⊥平面PDC；

（2）已知PD=AD=1，Q為棱l上的點，求PB與平面QCD所成角的正弦值的最大值．

試題評述 命題意圖是考查空間向量在證明立體幾何中的平行與垂直的位置關系，以及求線線角、線面角和面面角中的應用，屬于中檔題目．

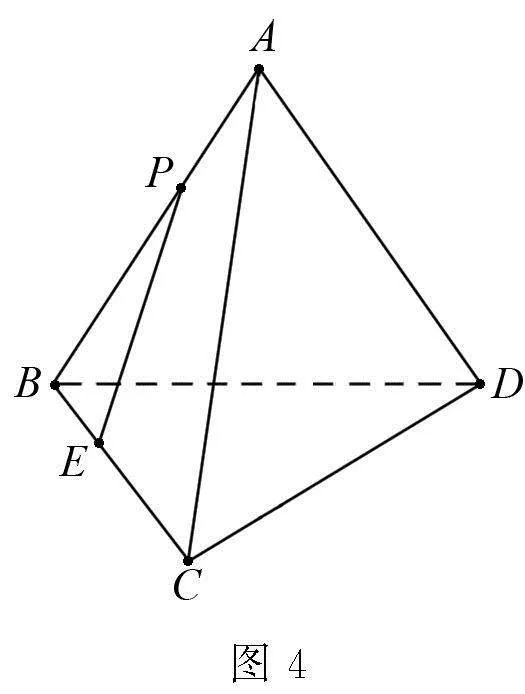
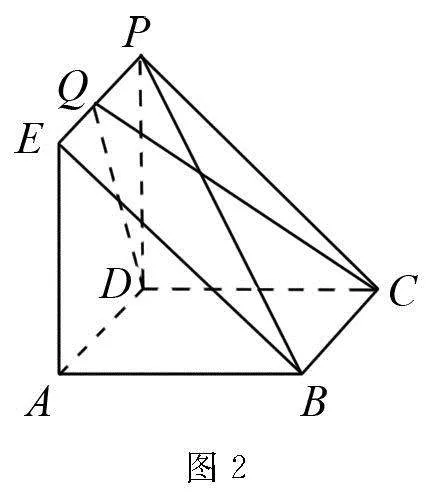
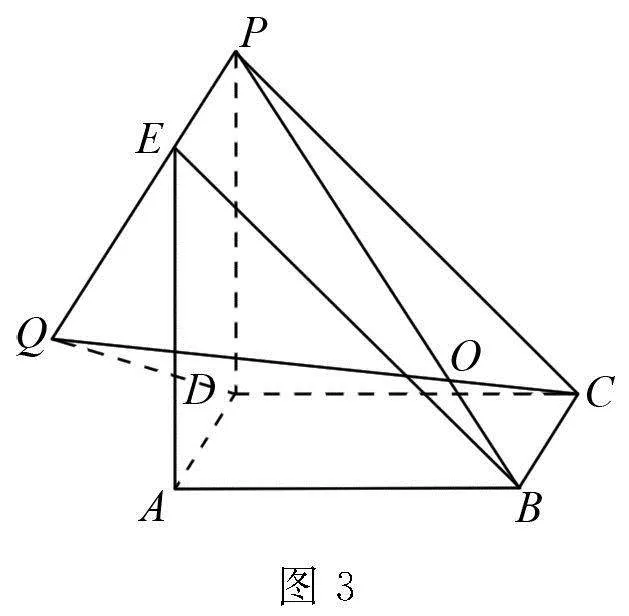
改造試題 如圖2，三棱柱ABE-CDP的面ABCD為正方形，PD⊥面ABCD．已知PD=AD=1，Q為棱PE上的點，求PB與平面QCD所成角的正弦值的最大值．

改造意圖 集中精力解決動態的線面角問題，優化解題教學結構，學會以靜制動的解題策略，破解立體幾何中的最值問題這個難點．對高考題進行微改造，一題多解，由薄到厚，拓展思維，使頭腦豐富而厚重；對解法進行微創新，使知識橫向、縱向聯系，跨越章節時空范疇，發揮高考題目復習帶動、輻射引領功能的最大化．最值問題是在點運動的過程中尋找出其邊界值．著眼于線面角的最大值引領學生展開探究，一是對目標函數的構建方式進行微探究，構造方式有常規作圖構造，補體轉移構造和坐標構造以及普通基底構造等；二是對最值解法進行微探究，打通知識壁壘，架起溝通橋梁，從重視應試教育到更注重核心素養培育，形成融會貫通格局和濃厚研究氛圍，多多挖掘試題內涵，對指導高三學生參加高考百利而無一害．

1 基于發揮試題復習功能，指導高三復習，一題多解，拓展思維

本文從一道高考題談起，從①數學解題是注重本源的，②數學解題是強調變化的，③數學解題是講究策略的這三個角

度各提供了3種共9種解法，已在《數理天地》高中版2021年第10期上發表，這里限于篇幅，就不再贅述．

二次思考 高考試題的命題意圖主要是考查學生空間向量坐標運算的掌握情況，發揮坐標定位在解決空間立體幾何最值問題中的優越性．本文命制了系列靜態題組，把學生分成6個小組各自完成其中一題，然后匯總結果，再觀察結果、歸納猜想、尋找規律，以期讓學生在求解靜態的線面角時徹底掌握基本解法，同時又能發現何時取得最值，領會知識形成過程，動態的最值學會靜態化思考，實現以靜制動．產生了如下教學策略，現展示出來供讀者研究時參考．

2 基于引領突破教學難點，探究命題規律，多題一解，以靜制動

開課時先復習空間向量的應用，線線角、面面角與線面角的向量表述公式形式高度統一．以下題目每組完成一題，預定時間10分鐘，10分鐘后分別找同學展示結果，把結果寫成一行，觀察大小變化是否有規律可尋．

變式6 如圖2，三棱柱ABE-CDP的面

3 基于借助規律鞏固成果，形成核心素養，類比探究，螺旋提升

數學核心素養是育人價值的集中體現，包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析．具體到這類試題，命題最終考查的是什么？是較高的邏輯推理和數學運算能力，也是選拔數學優等生的必然追求．以下設計的系列跟蹤訓練題目，多題歸一，思考其為何落點如此一致.理清問題實質．

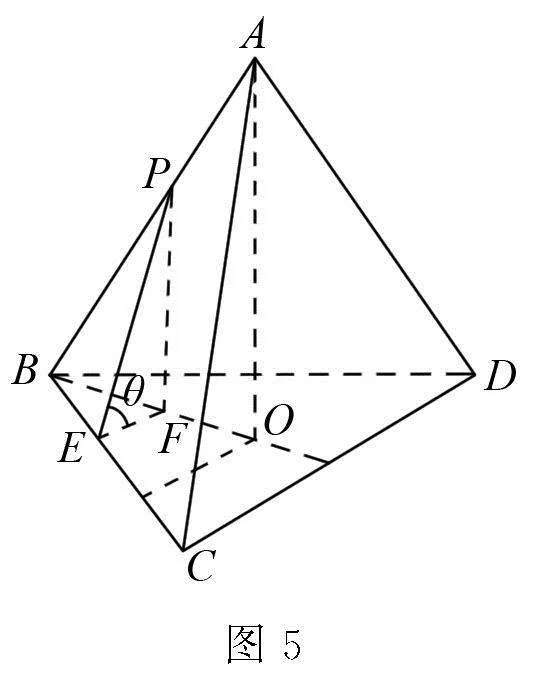
解析 作AO⊥平面BCD于點O，則點O是△BCD的中心，如圖5.

則∠PEF為所求的EP與平面BCD所成的角θ．

在△PBE中，由余弦定理得

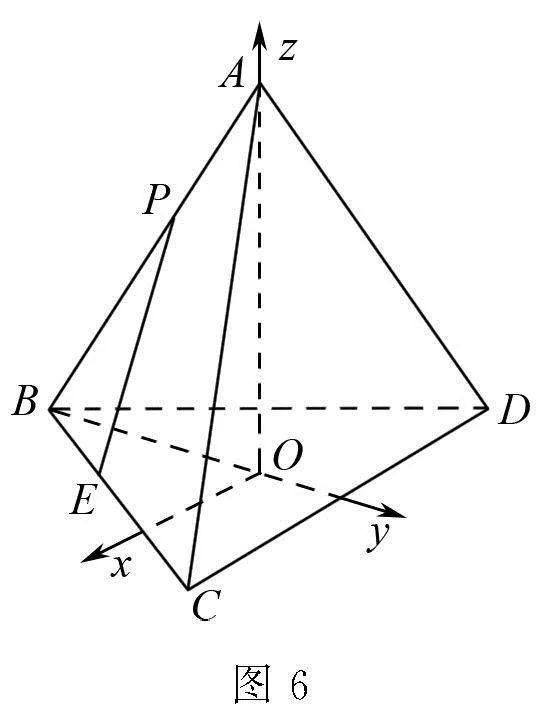
解析 建立如圖6所示的空間直角坐標系，設正四面體的棱長為3，

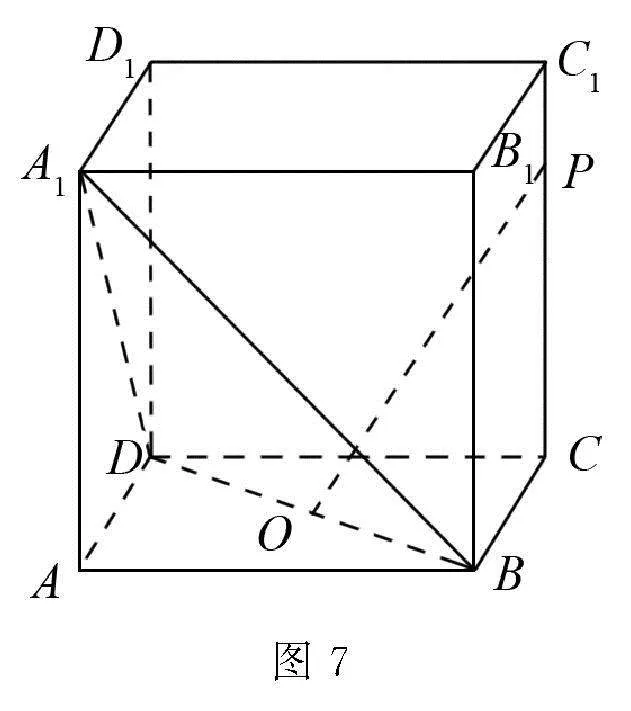
跟蹤訓練變式題 如圖7，在正方體ABCD-A1B1C1 D1中，點O為線段BD的中點，點P在線段CC1上．若直線OP與平面A1BD所成的角為θ，求sinθ的取值范圍．

4 結語

數學解題教學是數學教師以學生的解題學情為起點，高三學生和高一高二學生解題經驗、知識儲備、綜合素養等有著明顯的不同，需要教師以自身的解題經歷、經驗和研究為基礎區別對待．通過系列化題組設計，引領學生探究，促進深度思考，優化學生的思維品質．

【山東省教育教學研究課題“大單元視域下普通高中數學任務鏈進階驅動教學的實踐研究”2023JXY343的中期成果】

參考文獻：

[1]章建躍.理解學生 理解數學 理解教學 理解技術[J].中國數學教育（高中版），2010（12）：1-5．

[2]楊華文.從一道高考題談起[J].數理天地（高中版），2021（10）：22-25．