關于三角函數問題構建示例的探究

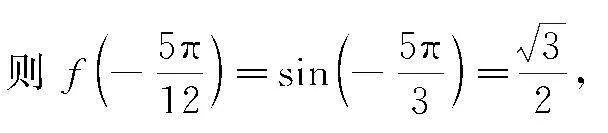
【摘要】三角函數是高中數學的知識重點，實際考查時常結合關聯知識綜合構建.問題解析建議開展命題分析，定位考點，再結合對應知識逐步剖析，必要時可繪制圖象，結合函數的周期圖象輔助分析.本文選取三角函數常見的三種構建情形，開展解題探究.

【關鍵詞】三角函數；高中數學；解題技巧

三角函數是高中數學的重點內容，探究學習中需要掌握三角函數的單調性、對稱性、周期等知識.問題考查構建形式多樣，常與其他知識相融合，變換設問情形，綜合考查學生的知識與能力.問題解析需要定位考點，結合知識要點逐步分析，下面結合考題舉例探究.

1 三角函數與零點

考題1 （2023年新高考I卷第15題）已知函數fx=cosωx－1（ω>0）在區間0，2π有且僅有3個零點，則ω的取值范圍是.

命題分析 本題目求三角函數的參數取值，核心條件為“在區間0，2π有且僅有3個零點”，顯然考點為三角函數與零點.解題的關鍵是把握零點定義，轉化條件信息，即令f（x）=0，得cosωx=1有3個根.后續可結合余弦函數的圖象性質求解.

過程解析 因為0≤x≤2π，

所以0≤ωx≤2ωπ.

令f（x）=0，

得cosωx=1有3個根.

令t=ωx，

則cost=1有3個根，其中t∈［0，2ωπ］.

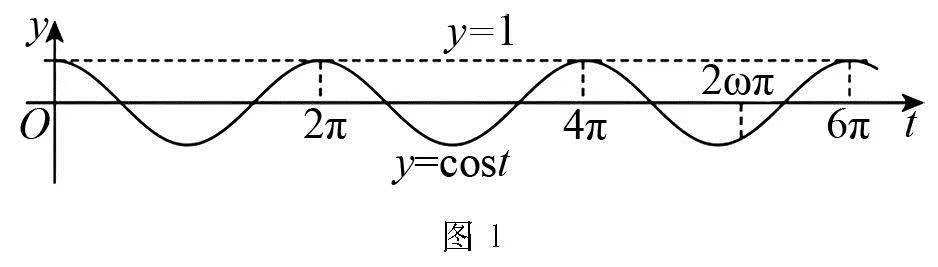
繪制如圖1所示圖象，由y=cost的圖象性質可得4π≤2ωπ<6π，故2≤ω<3，

故答案為［2，3）.

解后評析 三角函數與零點問題較為常見，解題的關鍵有三點：一是理解零點的定義，掌握求解思路和轉化方法；二是靈活繪制圖象，結合圖象直觀分析；三是關注圖象的周期變化，靈活變通調整變量.

2 三角函數與對稱

命題分析 本題目要求解三角函數值，核心條件有兩個：一是關于函數在區間上的單調性；二是關于函數的對稱軸，顯然為三角函數與單調性和對稱性的綜合問題.解題的關鍵是靈活使用三角函數的屬性知識，結合題意合理轉化.

故答案為（D）.

解后評析 上述將三角函數的圖象、單調性、對稱性交匯考查，構建了綜合性較強的三角函數求值問題.探究解析的關鍵有兩點：一是掌握基于y=Asin（ωx+φ），x∈R的圖象求解析式的步驟；二是掌握三角函數關于直線的對稱轉化方法.

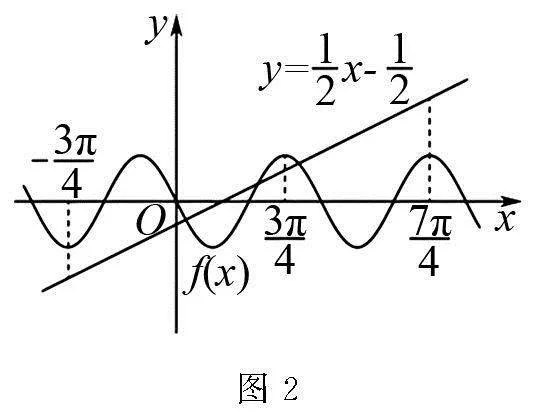
3 三角函數與平移

（A）1. （B）2. （C）3. （D）4.

解后評析 上述題目設定三角函數平移，求解平移后函數與直線的交點個數，綜合性較強，該類問題建議結合圖象分析.探究學習時注意知識總結：一是總結函數圖形變換的方法步驟；二是掌握三角函數與直線相交的處理方法，注意特殊位置的大小比較.

4 結語

總之，三角函數問題是高考重點問題，探究學習中建議分三個階段：階段一，掌握基礎知識，深刻理解其圖象與性質屬性；階段二，開展拓展探究，構建知識關聯，總結常見問題類型；階段三，總結方法策略，結合實例強化訓練.