高中數學教學中圓錐曲線解題方法的研究



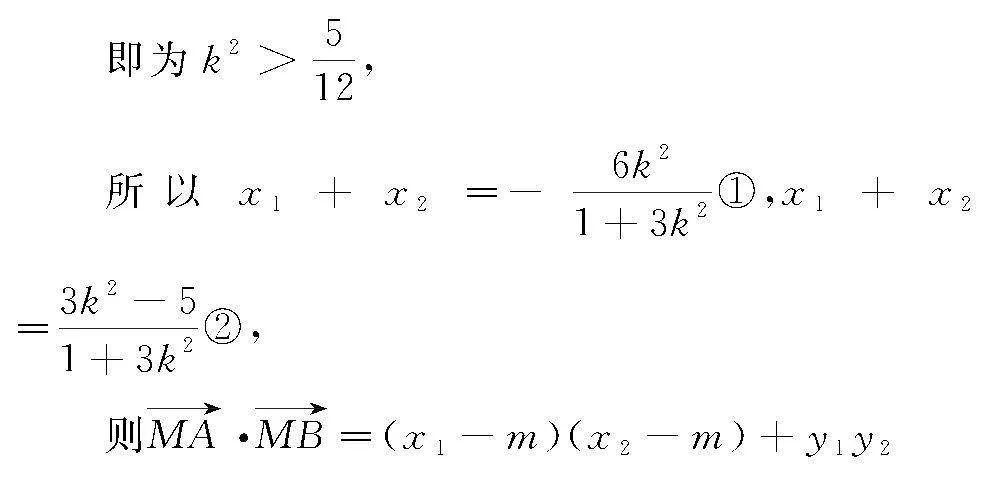



【摘要】解題訓練屬于高中數學教學中的常設環節,其中圓錐曲線題型靈活多變,難度較大,為提升學生的解題能力,教師需注重相關題型的介紹與對應解題方法的講解,使其遇到相關習題時可以迅速破題,增強他們解答圓錐曲線類試題的自信心,為高考做準備.本文以高中數學教學中圓錐曲線解題方法為研究對象,同時分享一系列解題案例以供參考所用.
【關鍵詞】高中數學教學;圓錐曲線;解題方法
圓錐曲線這一部分的知識較為特殊,以研究橢圓、雙曲線和拋物線這三類圓錐曲線與方程為主,兼具幾何與代數的雙重特征,對學生的學習能力與解題能力均要求較高.在高中數學解題教學中,教師可圍繞圓錐曲線題目設計專題訓練,帶領學生學習一些比較常用的解題方法,使其能用來有效解答圓錐曲線題目,由此提高他們解答圓錐曲線試題的水平.
1 運用方程解題方法,解答圓錐曲線位置問題
在高中數學解題教學中,經常會遇到判斷直線和圓錐曲線的位置類試題,需要將直線和圓錐曲線的方程聯立起來,轉化成一元二次方程,運用方程解題方法,借助Δ進行判斷.同時,還應注重靈活運用向量知識判斷直線關系,如果題目中沒有提示直線斜率是否存在,解題時還應注重展開分類討論,不能遺漏任何一種滿足題干要求的情形,確保對問題考慮的全面性[1].
分析 (1)可采用方程法,直接將橢圓和直線的方程聯立起來進行化簡,求出k的取值范圍;(2)可結合方程及其他數學知識完成求解.
2 借助假設解題方法,解答圓錐曲線定值問題
針對高中數學圓錐曲線解題教學來說,求解定值類問題較常見.教師可以指引學生借助假設法進行解題,先結合已知條件把方程列出來,借助一元二次方程根和系數之間的關系,對要求解的定值表達式展開化簡,讓他們找到適當的切入點進行假設,使其通過假設列出相應的式子,如果表達式中帶有參數,為保證其值為定值要將帶參數的部分給消除[2].
分析 處理這類試題時,要先假設這樣的點M存在,再根據題干中提供的條件進行分析和計算,如果不會出現沖突則說明該點的確存在,假如出現矛盾則說明該點不存在.
詳解 假設在x軸上存在這樣的一點M(m,0)滿足題意,設A(x1,y1),B(x2,y2),
當直線AB的斜率存在,設為k,則對應的直線方程為y=k(x+1),將其同橢圓方程的聯立起來消去y,由此得到(1+3k2)x2+6k2x+3k2-5=0,
則Δ=36k4-4(1+3k2)(3k2-5)>0,
=(x1-m)(x2-m)+k2(1+x1)(1+x2)
=(1+k2)x1x2+(k2-m)(x1+x2)+k2+m2,
將①②代入整理得到
當直線AB的斜率不存在時,其和x軸垂直,
3 結語
總而言之,圓錐曲線試題是高中數學考試中容易拉開分差的一類題型,教師應結合具體例題剖析不同題型的解題方法,帶領學生進行針對性解題訓練,要求他們做好解題的總結與反思工作,使其真正把握不同題型的解題規律和技巧,從而能夠攻克這一難點題型.
參考文獻:
[1]趙偉.高中數學圓錐曲線解題教學模式研究[J].數理天地(高中版),2023(19):30-32.
[2]朱新保.關于一道圓錐曲線問題的解析探究與思考[J].數學教學通訊,2023(18):86-88.
[3]馬利民.高中數學教學中圓錐曲線的解題方法[J].數理天地(高中版),2023(11):33-34.

