周期復合材料二次特征值問題的二階雙尺度分析與計算




摘 要: 對周期復合域的二次特征值問題(Quadratic Eigenvalue Problem,QEP),本文提出了一種二階雙尺度(Second-Order Two-Scale,SOTS)漸近分析和計算方法. 該方法考慮一種包含速度阻尼的典型QEP,對特征函數進行漸近展開并設計了有限元算法,采用線性化方法求解均勻化二次特征值問題. 數值算例表明,該方法可以有效處理此類非線性特征值問題,且二階校正器在描述特征函數的局部行為和高效獲得特征值的逼近值等方面起著重要作用.
關鍵詞: 周期復合域; 二次特征值問題; 二階雙尺度分析
中圖分類號: O241. 82 文獻標志碼: A DOI: 10. 19907/j. 0490-6756. 2024. 041007
1 引言
在許多結構中,線性特征值足以表示結構的固有模態和頻率. 盡管如此,當振動模型含有阻尼效應時,就需要考慮二次特征值問題(Quadratic EigenvalueProblem, QEP)[ 1]. 此外,二次特征值問題還在許多方面有其應用,如聲學器件的線性振蕩[2, 3]、流體的線性穩定性分析[4, 5]、信號自回歸過程[6],等. Eisenfeld[7]證明二次特征值問題解的存在性并研究了解的特征. Tisseur 和Meerbergen[1]研究了二次特征值問題的一些應用、數學性質及數值分析. Walsh 等[8]提出了求解二次特征值問題的算法.Higham 等[9]則研究了二次特征值問題數值解的穩定性.
隨著對于各種工業應用復合材料需求的不斷涌現,對強異質材料的光譜特性進行研究顯得十分必要和迫切. 在求解含有兩個或兩個以上成分組成的復合材料上的二次特征值問題時,為了提高計算效率人們引入了均勻化策略,用多尺度建模來描述其宏觀行為,并利用漸近展開方法來捕捉各種數學、物理和機械問題的局域振蕩細節[10]. Marchenko等[11]首次提出了多尺度漸近展開法,該方法在材料系數快速振蕩的周期結構研究中發揮重要作用. 理論上,Nguetseng[12]和Allaire[13]引入并發展了雙尺度收斂的概念,驗證了多尺度擴展技術的有效性.這種漸近分析同樣適用于復合域中的特征值問題.Kesavan[14, 15]引入“修正方程”的思想,得到了效果很好的特征函數和特征值的漸近展開式. Cui 等[16]系統地導出了二階雙尺度(Second-Order Two-Scale,SOTS )漸近展開式,以便在實際計算中準確快速地捕捉原始解的強振蕩. 在此基礎上,我們還將SOTS 方法應用于Steklov 彈性特征值問題以及曲線坐標系中多孔材料模型特征值問題[17, 18].
本文研究周期復合材料模型的二次特征值問題. 我們先進行理論分析,然后給出數值算例驗證二階雙尺度方法在復合材料上的二次特征值問題的有效性. 除非特別指出,本文中均使用Einstein 求和約定,即重復指標表示求和.
2 二次特征值問題
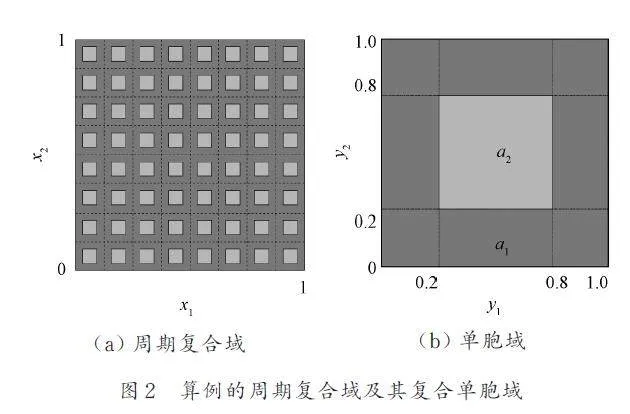
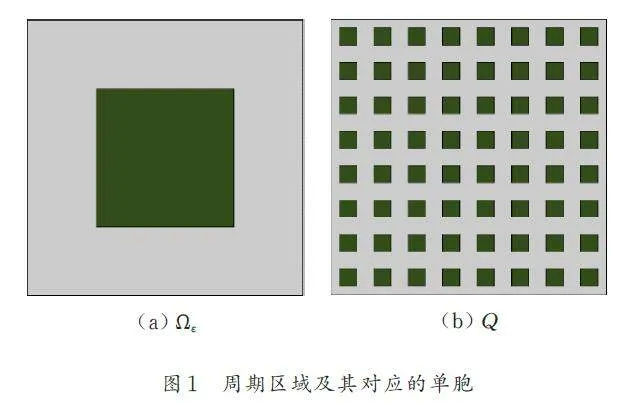
考慮周期復合材料Ωε 由多種材料組成,如圖1a所示,對應的單胞Q 如圖1b 所示.
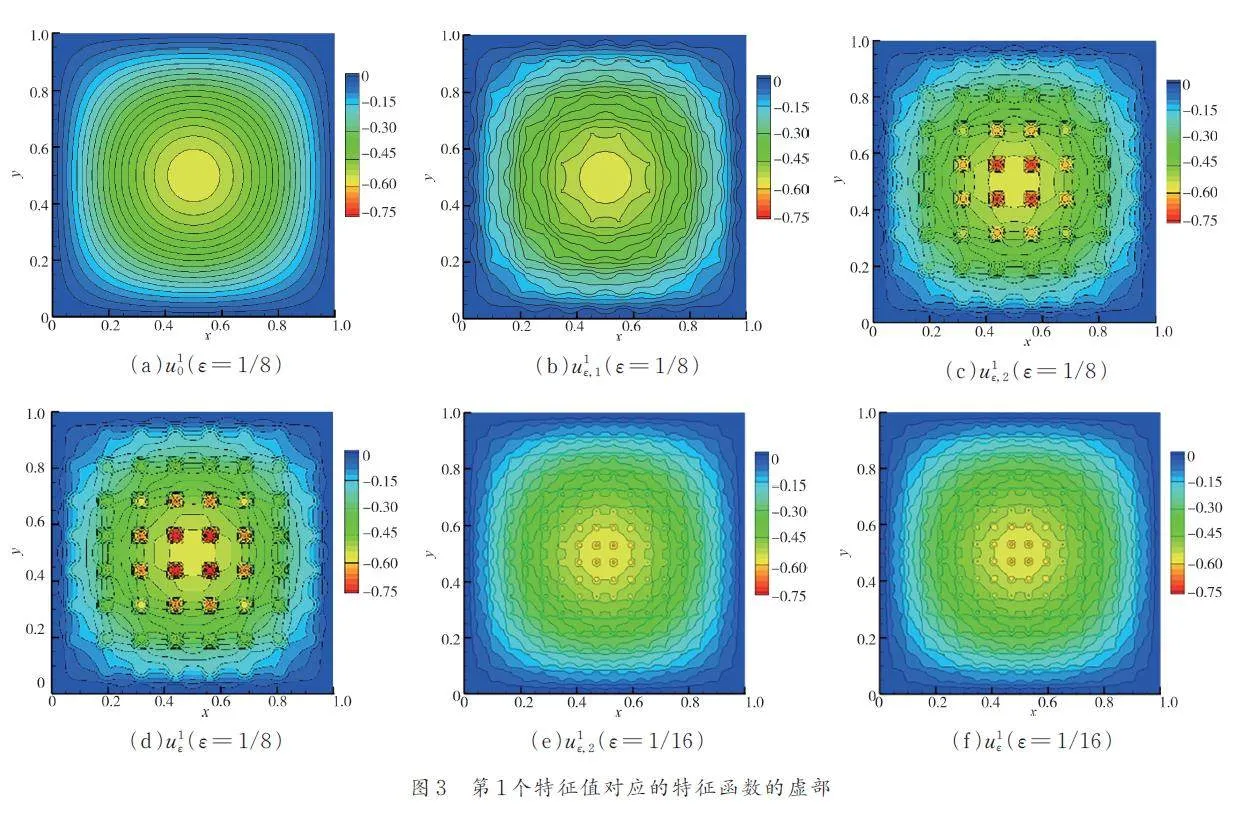
在得到單胞域Q 上的一階單胞函數Np 后,可以計算出均勻系數m0、c0 和k 0ij 為k 0ij = k0 δij, k0 =0. 609 84, m0 = 0. 7612, c0 = 0. 3756. 由于原問題的精確解難以求出,這里將在原宏觀區域細網格下計算得到的解作為精確解與各階逼近解進行比較.從圖3 中可以看出,均勻解u10比較光滑,足以描述原始解的宏觀特征. 添加一階校正器u11可以更好地描述域Ωε 內的振蕩,但不夠顯著,因而有必要添加二階校正器u12 來捕捉更多的微觀特征. 因此,我們可以說均勻解也是特征函數的適當近似. 此外,通過對比圖3(c~f)可以觀察到,隨著ε 的減小SOTS 近似解將更接近精確解.
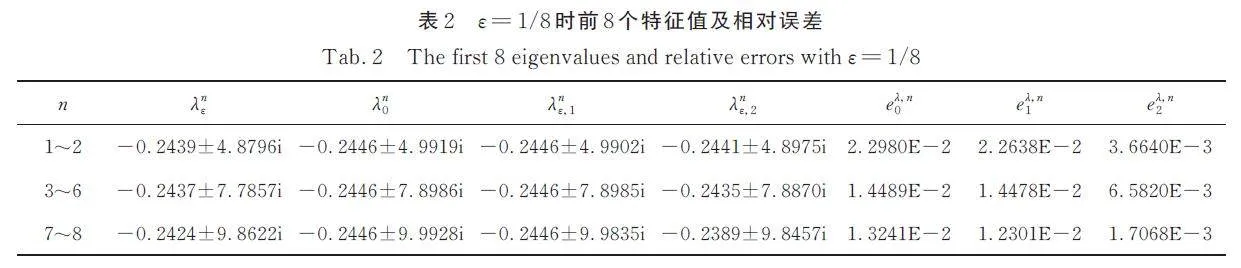
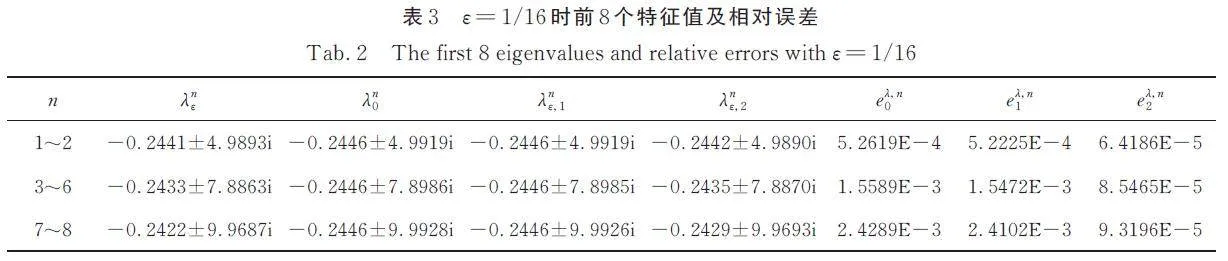
根據式(13)和式(14)中λi1 和λi2 的積分表達式,表3 和表4 分別列出了當ε = 1/8 和ε = 1/16 時前8個特征值的計算近似值. 可以看出,均勻解λi0 與λiε十分接近,加上一階校正器后兩者差別不大,通過添加二階校正器λiε,2 得到了顯著改進結果. 隨著ε 的減小,特征值近似值和精確值之間的誤差減小,注意到eλ,i2 減小最快,這與理論結果相一致.
6 結論與展望
本文首先將SOTS 表達式應用于具有周期復合域的二次特征值問題,定義了一系列單胞函數,得到了均勻均勻化QEP 問題. 在此基礎上,對漸近解進行組裝,以捕獲更多的微觀特征. 同時,通過引入輔助函數,先后得到特征值的FOTS解和SOTS解,并建立特征值的誤差估計. 進一步, 我們建立了基于SOTS的有限元算法. 最后,數值算例表明,本文提出的方法能有效模擬原始二次特征值問題的特征函數和特征值.
參考文獻:
[1] Tisseur F, Meerbergen K. The quadratic eigenvalueproblem[ J]. SIAM Rev, 2001, 43: 235.
[2] Bermúdez A, Durán R G, Rodríguez R, et al. Finiteelement analysis of a quadratic eigenvalue problemarising in dissipative acoustics [J]. SIAM J NumerAnal, 2000, 38: 267.
[3] Pierce A D, Beyer R T. Acoustics: An introductionto its physical principles and applications [M]. NewYork: McGraw-Hill, 1990.
[4] Hall P, Malik M R, Poll D I A. On the stability of aninfinite swept attachment line boundary layer [J]. PRoy Soc London A, 1984, 395: 229.
[5] Theofilis V. Spatial stability of incompressibleattachment-line flow [J]. Theor Comput Fluid Dy,1995, 7: 159.
[6] Davila C E. A subspace approach to estimation of autoregressiveparameters from noisy measurements[ J].IEEE T Signal Proc, 1998, 46: 531.
[7] Eisenfeld J. Quadratic eigenvalue problems [J]. JMath Anal Appl, 1968, 23: 58.
[8] Walsh T F, Day D M. Quadratic eigenvalue problems[R]. Albuquerque: Sandia National Laboratories,2007.
[9] Higham N J, Mackey D S, Tisseur F, et al. Scaling,sensitivity and stability in the numerical solution ofquadratic eigenvalue problems [J]. Int J Numer MethEng, 2008, 73: 344.
[10] Cioranescu D, Donato P. An introduction to homogenization[M]. New York: Oxford University Press,1999.
[11] Marchenko V A, Khruslov E Y. Boundary-valueproblems with fine-grained boundary [J].Matematicheskii Sbornik, 1964, 107: 458.
[12] Nguetseng G. A general convergence result for a functionalrelated to the theory of homogenization [J].SIAM J Math Anal, 1989, 20: 608.
[13] Allaire G. Homogenization and two-scale convergence[ J]. SIAM J Math Anal, 1992, 23: 1482.
[14] Kesavan S. Homogenization of elliptic eigenvalueproblems( I)[ J]. Appl Math Optim, 1979, 5: 153.
[15] Kesavan S. Homogenization of elliptic eigenvalueproblems( II)[ J]. Appl Math Optim, 1979, 5: 197.
[16] Cui J Z, Cao L Q. Finite element method based ontwo-scale asymptotic analysis [J]. Chin J NumerMath Appl, 1998, 20: 60.
[17] Tan L Q, Ma Q, Hu B, Multiscale asymptotic analysisfor Steklov elastic eigenvalue problem in periodicallyperforated domain [J]. J Sichuan Univ(Nat SciEd), 2022, 59: 011002.[譚理琴,馬強,胡兵. 周期多孔結構的Steklov彈性特征值問題的多尺度漸近分析[J].四川大學學報(自然科學版), 2022, 59: 011002.]
[18] Ye S Y, Ma Q, Hu B. Second order two scale calculationfor eigenvalue problem of porous materialmodel in curvilinear coordinates [J]. J Sichuan Univ(Nat Sci Ed), 2021, 58: 031004.[葉舒愉,馬強,胡兵. 曲線坐標下多孔材料模型特征值問題的二階雙尺度計算方法[J]. 四川大學學報( 自然科學版),2021, 58: 031004.]
[19] Vanninathan M. Homogenization of eigenvalue problemsin perforated domains [J]. P Indian AS-MathSci, 1981, 90: 239.
(責任編輯: 周興旺)
基金項目: 國家自然科學基金(11801387, 11971336, 11971337); 四川省自然科學基金(2022NSFSCO322); 中央高校基本科研業務費專項資金(YJ201811)

