巧抓核心　探尋解法

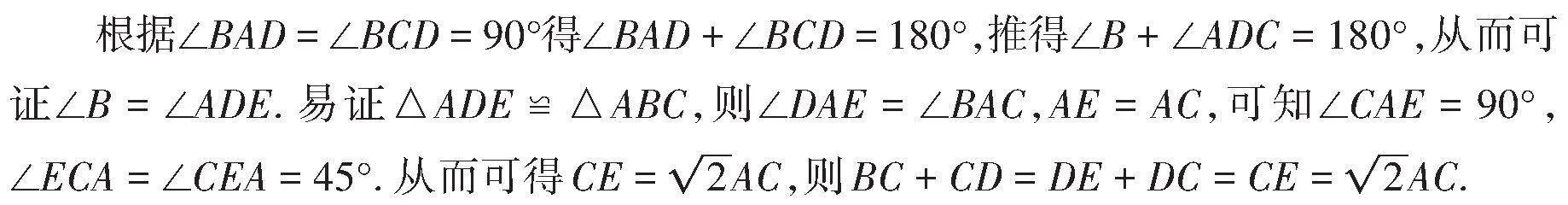
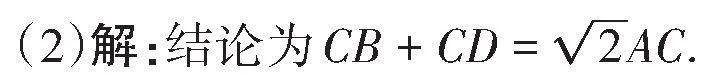
原題再現

例 【思維探究】

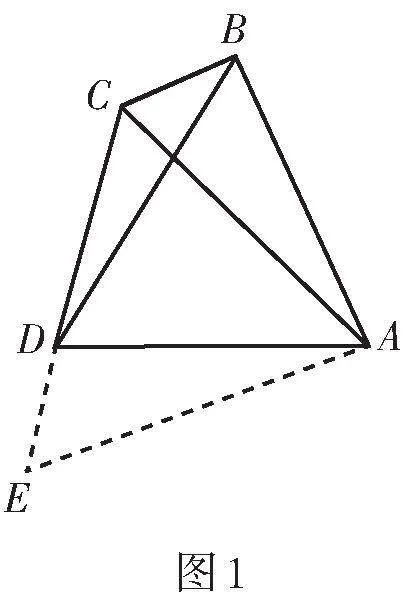
（1）如圖1，在四邊形ABCD中，∠BAD = 60°，∠BCD = 120°，AB = AD，連接AC.

求證：BC + CD = AC.

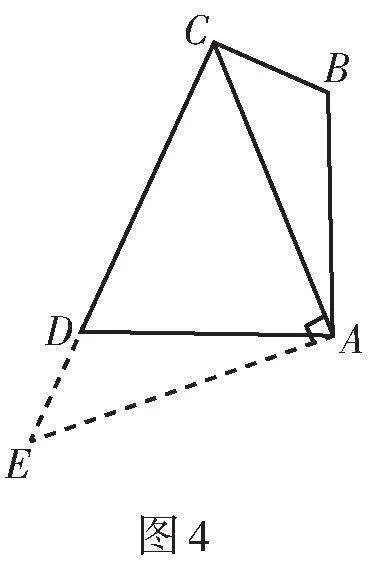
小明的思路是：延長CD到點E，使DE = BC，連接AE. 根據∠BAD + ∠BCD = 180°，推得∠ABC + ∠ADC = 180°，從而得到∠ABC = ∠ADE，然后證明△ADE ≌ △ABC，從而可證BC + CD = AC，請你幫助小明寫出完整的證明過程.

【思維延伸】

（2）如圖2，四邊形ABCD中，∠BAD = ∠BCD = 90°，AB = AD，連接AC，猜想BC，CD，AC之間的數量關系，并說明理由.

【思維拓展】

破解策略

本文僅就問題（2）和問題（3）進行探究.

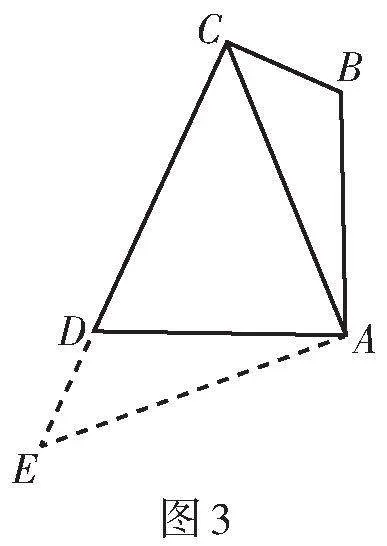
解法1：如圖3，延長CD到點E，使DE = BC，連接AE.

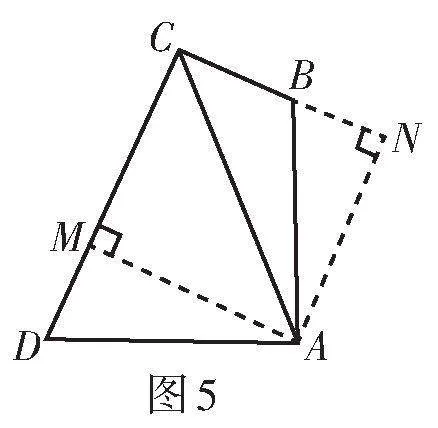
解法3：如圖5，過點A作AM ⊥ CD于點M，AN ⊥ CB交CB的延長線于點N.

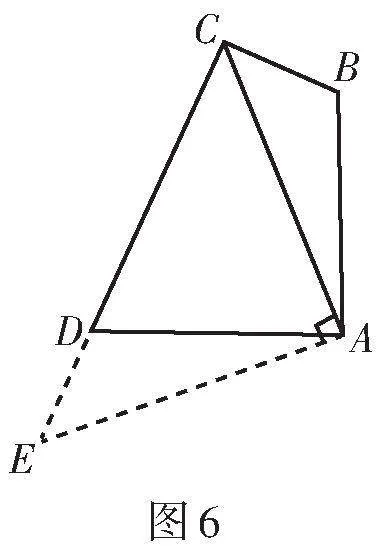
解法4：如圖6，將△ABC繞點A逆時針旋轉90°至△ADE.

a. 當∠CDA = 75°時.

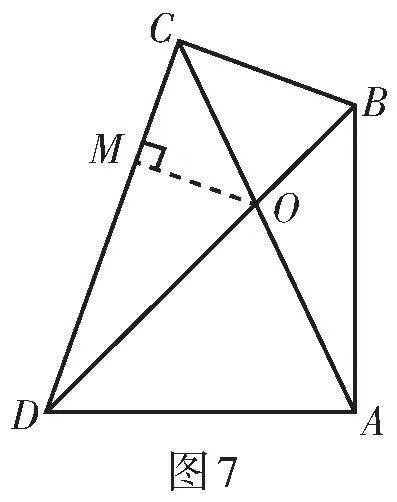
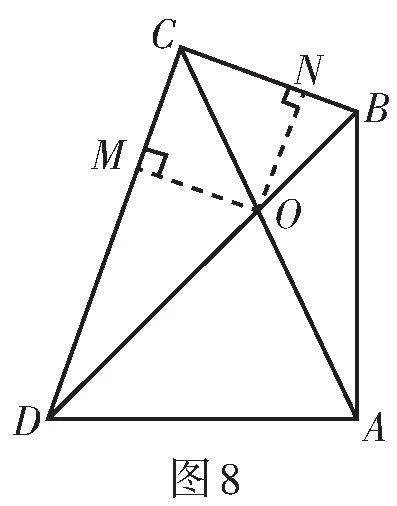
解法1：如圖7，過點O作OM ⊥ CD于點M.

b. 當∠CBA = 75°時.

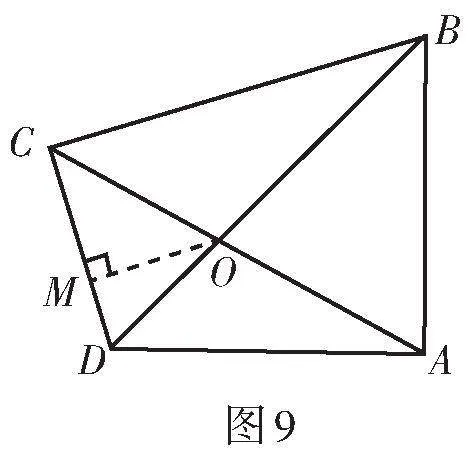
解法1：如圖9，過點O作OM ⊥ CD于點M.

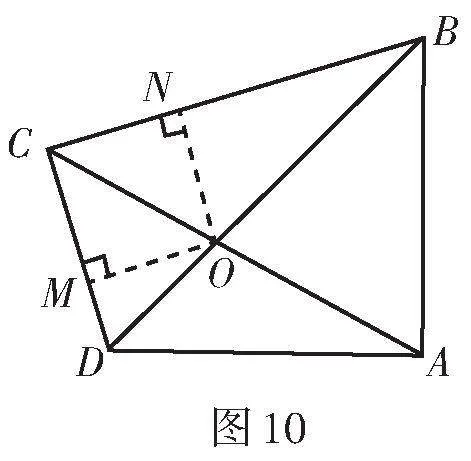
解法2：如圖10，過點O作OM ⊥ CD于點M，ON ⊥ CB于點N.

勤于積累

“旋轉出等腰，等腰可旋轉”，當問題中出現“共頂點，等線段”結構時，可考慮利用“造旋轉，出全等”這一解題策略，化分散為集中，化不規則為規則. 若用旋轉作輔助線，則需證明三點共線，如問題（2）的解法4；若采用截長補短、作雙垂線等方法，則需證明全等，如問題（2）的解法1、解法2、解法3. 不同解法殊途同歸，各具優點.

拓展訓練

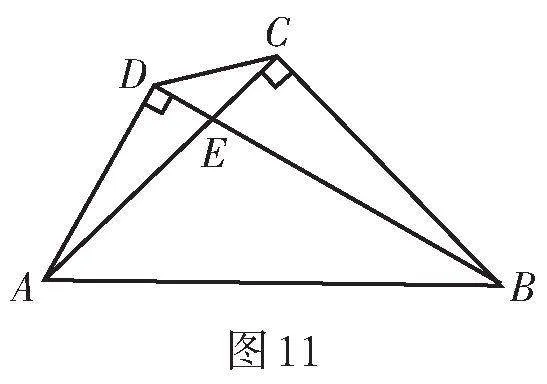
1. 如圖11，在四邊形ABCD中，對角線AC，BD相交于點E，AC = BC = 6 cm，∠ACB = ∠ADB = 90°. 若BE = 2AD，則△ABE的面積是 cm2，∠AEB = °.

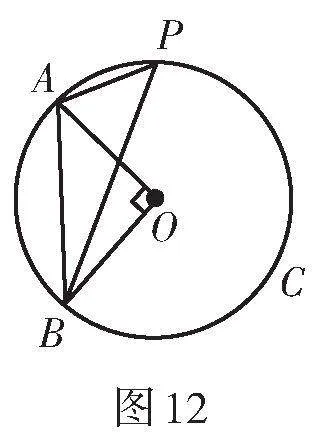
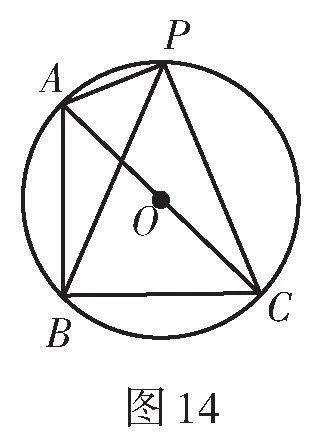
2. 【感知】如圖12，點A，B，P均在⊙O上，∠AOB = 90°，則銳角∠APB的大小為 度.

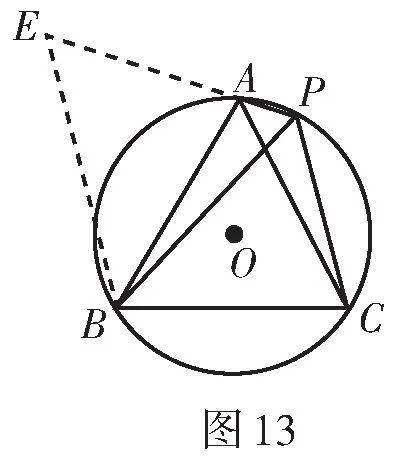
證明：延長PA至點E，使AE = PC，連接BE.

∵四邊形ABCP是⊙O的內接四邊形，

∴∠BAP + ∠BCP = 180°.

∵∠BAP + ∠BAE = 180°，

∴∠BCP = ∠BAE.

∵△ABC是等邊三角形，

∴BA = BC.

∴△PBC ≌ △EBA（SAS）.

請你補全余下的證明過程.

答案：1. （36 - 18[2]），112.5 2. 45，證明略，[223]