基于轉矩跟蹤電流誤差校正的壓縮機轉速脈動抑制算法研究

摘 "要：針對空調用永磁壓縮機在低頻運行中存在轉速脈動大、振動噪聲高等問題，提出一種基于轉矩跟蹤電流誤差校正的壓縮機轉速脈動抑制算法。首先，對壓縮機的周期性轉速脈動進行分析，并根據轉速脈動特性建立轉速環控制系統模型。然后，引入迭代學習算法，獲得轉矩跟蹤電流，在此基礎上，提出特征濾波函數，用來提取轉矩跟蹤電流基波分量，有效抑制特定次頻率的轉速脈動，同時引入轉矩跟蹤電流誤差校正律，對轉矩跟蹤電流與參考交軸電流的誤差進行校正，進一步獲得前饋補償電流，并施加到參考交軸電流中，該算法可以消除傳統迭代學習轉矩跟蹤電流存在的誤差累積，跟蹤性能好。最后，在空調壓縮機實驗平臺上對算法進行驗證，實驗結果表明，采用該算法可以顯著抑制壓縮機的轉速脈動。

關鍵詞：壓縮機系統；低頻轉速脈動；特征濾波函數；轉矩跟蹤電流誤差校正律；迭代學習

DOI：

中圖分類號：TM351 " " " " " 文獻標志碼：A " " " " "文章編號：

Research on speed ripple suppression algorithm of compressor motor based on torque tracking current error correction

YANG Zhebin1， DENG Rongfeng1， ZHANG Xiaojun1， YANG Jiaqiang1， GU Tangtang2，

ZHUO Senqing2

（1. College of Electrical Engineering， Zhejiang University， Hangzhou 310027， China;

2. Ningbo AUX Electrical Limited Company， Ningbo 315191， China）

Abstract： The speed ripple suppression algorithm of compressor motor based on torque tracking current error correction is proposed to address the issues of large torque ripple and high vibration noise in the operation of a permanent magnet compressor for air conditioning. Initially， based on the characteristics of the torque ripple， an analysis of the compressor's periodic speed ripple is conducted. The iterative learning control approach is employed to obtain torque tracking current. On this basis， the optimized filtering function is introduced to extract the fundamental component of the torque tracking current. At the same time， the torque tracking current error correction law is introduced to correct the error between the torque tracking current and the reference torque current， and the feedforward compensation current is obtained and fed forward to the control system. The error accumulation of traditional iterative learning torque tracking current is eliminated， and the compressor speed ripple is effectively suppressed. Finally， The algorithm is validated on an experimental platform for air conditioning compressors， and the experimental results demonstrate effectively mitigating compressor torque ripple.

Keywords： compressor system; low frequency speed ripple; characteristic filter function; torque tracking current error correction law; iterative learning

0 引 "言

目前，壓縮機作為空調系統的主要核心部件，其內部電機采用永磁同步電機（permanent magnet synchronous motor， PMSM），與其他電機相比，具有功率因數高、運行性能好等優點[1-4]。然而空調行業為了降低成本通常采用單轉子壓縮機，由于不對稱曲軸設計，在一個周期內受到吸氣壓縮、吸氣排氣的影響，導致負載產生周期性轉矩脈動，從而引起壓縮機的周期性轉速脈動。

壓縮機轉速脈動一直是空調行業的關鍵技術難題，容易造成系統振動與噪聲，所以必須采取有效措施對轉速脈動進行抑制，目前常見方法有電機優化設計[5]，對電機本體進行斜槽、斜極設計，但是針對單轉子壓縮機的負載特性，這種轉速脈動抑制效果較差；另一種是電機優化控制[6-7]，通過控制電機參考交軸電流，實現電磁轉矩的補償，最終達到轉速脈動抑制效果。

為了抑制空調壓縮機轉速脈動，國內外學者針對壓縮機優化控制方法進行了大量的研究。文獻[8-9]提出傅里葉變換補償法，對轉速進行傅里葉分解，提取轉速基波量進行補償。該方法需要進行查表離線補償，不同類型的壓縮機初始相位不一致，需要對初始相位進行調節，算法通用性差。文獻[10-12]提出重復控制補償算法，可用于跟蹤或消除周期信號的誤差，通過補償控制延遲來實現周期性擾動抑制，但是該方法只能針對固定運行頻率進行擾動抑制，當運行頻率改變時，需要重新調整參數。文獻[13-15]提出負載轉矩觀測算法，觀測器可以對擾動轉矩進行前饋補償，夠實時觀測電機受到的時變且難以預測的擾動。但是觀測出的負載轉矩存在一定的相位延遲，且對于電機模型參數的依賴性較高。文獻[16-17]提出迭代學習控制算法，獲得轉矩跟蹤電流，并前饋到控制系統。這種方法對于周期性轉速脈動抑制效果好，但獲得的轉矩跟蹤電流存在誤差累積。文獻[18]提出基于分數階比例微分迭代學習控制算法（proportional differential iterative learning control， PDILC），系統的高頻諧波分量得到補償，有效抑制周期性轉速脈動，但是分數階的參數配置復雜且容易造成參數攝動。文獻[19]引入無模型自適應迭代學習算法，擺脫對于精確模型的依賴，但是算法復雜，程序執行時間長。在實際工況中，受到溫度、環境等因素的影響，導致上述文獻[16-19]的迭代學習控制算法獲得的轉矩跟蹤電流補償量均存在誤差累積，壓縮機轉速脈動抑制效果受限。

在上述文獻研究的基礎上，本文提出一種基于轉矩跟蹤電流誤差校正的壓縮機轉速脈動抑制算法（error correction iterative learning control， ECILC），首先對壓縮機轉速脈動的各次脈動分量進行分析，建立轉速環控制系統模型。在迭代學習基礎上，提出特征濾波函數，分析擾動項的零極點分布，提取轉矩跟蹤電流基波分量，參數配置遵循零極點對消原則，該方法與傳統迭代學習算法相比，對于特定次頻率的轉速脈動抑制效果顯著，算法跟蹤性能好。同時引入轉矩跟蹤電流誤差校正律，對轉矩跟蹤電流進行校正，獲得前饋補償電流，并施加到參考交軸電流中，消除了傳統迭代學習轉矩跟蹤電流存在的誤差累積，無需查表離線補償，參數適應性強，算法穩定性能好。最后在壓縮機實驗平臺上驗證了算法控制策略的有效性，實驗結果表明，采用該算法能有效抑制壓縮機低頻轉速脈動。

1.1 壓縮機轉速脈動分析

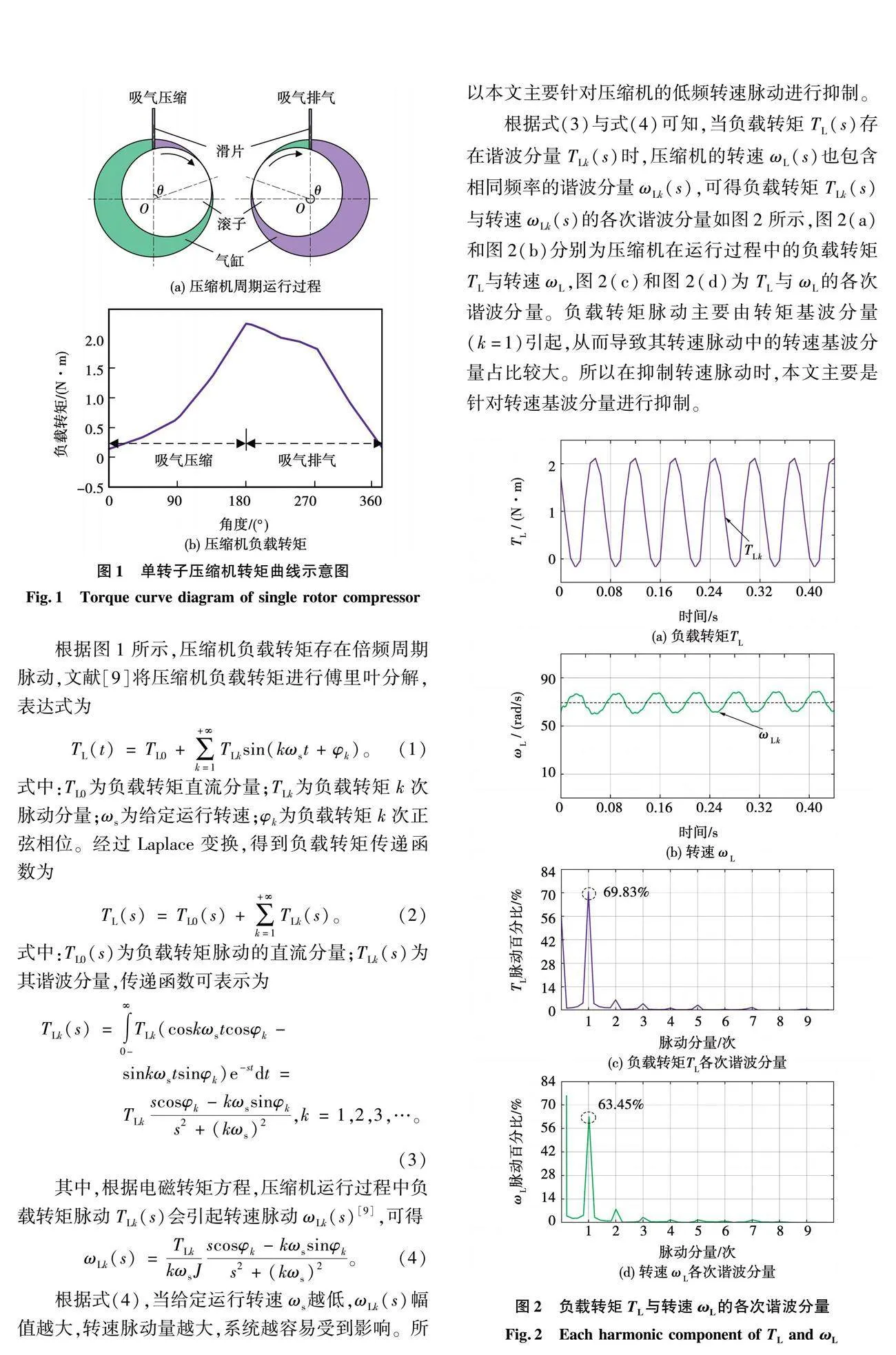
單轉子壓縮機采用不對稱曲軸設計，在一個周期內受到吸氣壓縮、吸氣排氣的影響，產生不同的氣體阻力，導致壓縮機負載產生周期性的轉矩脈動。單轉子壓縮機轉矩曲線如圖1所示，圖1（a）和圖1（b）分別為壓縮機周期運行過程（吸氣壓縮、吸氣排氣）與壓縮機負載轉矩。

根據圖1所示，壓縮機負載轉矩存在倍頻周期脈動，文獻[9]將壓縮機負載轉矩進行傅里葉分解，表達式為

。 （1）

式中：TL0為負載轉矩直流分量；TLk為負載轉矩k次脈動分量；ωs為給定運行轉速；φk為負載轉矩k次正弦相位。經過Laplace變換，得到負載轉矩傳遞函數為

。 （2）

式中：TL0（s）為負載轉矩脈動的直流分量；TLk（s）為其諧波分量，TLk（s）的傳遞函數可表示為

。 （3）

其中，根據電磁轉矩方程，壓縮機運行過程中負載轉矩脈動TLk（s）會引起轉速脈動ωLk（s）[9]，可得

。 （4）

根據式（4），當給定運行轉速ωs越低，ωLk（s）幅值越大，轉速脈動量越大，系統越容易受到影響。所以本文主要針對壓縮機的低頻轉速脈動進行抑制。

根據式（3）與式（4）可知，當負載轉矩TL（s）存在諧波分量TLk（s）時，壓縮機的轉速ωL（s）也包含相同頻率的諧波分量ωLk（s），可得負載轉矩TLk（s）與轉速ωLk（s）的各次諧波分量如圖2所示，圖2（a）和圖2（b）分別為壓縮機在運行過程中的負載轉矩TL與轉速ωL，圖2（c）和圖2（d）為TL與ωL的各次諧波分量。負載轉矩脈動主要由轉矩基波分量（k=1）引起，從而導致其轉速脈動中的轉速基波分量占比較大。所以在抑制轉速脈動時，本文主要是針對轉速基波分量進行抑制。

1.2 永磁同步壓縮機轉速閉環控制

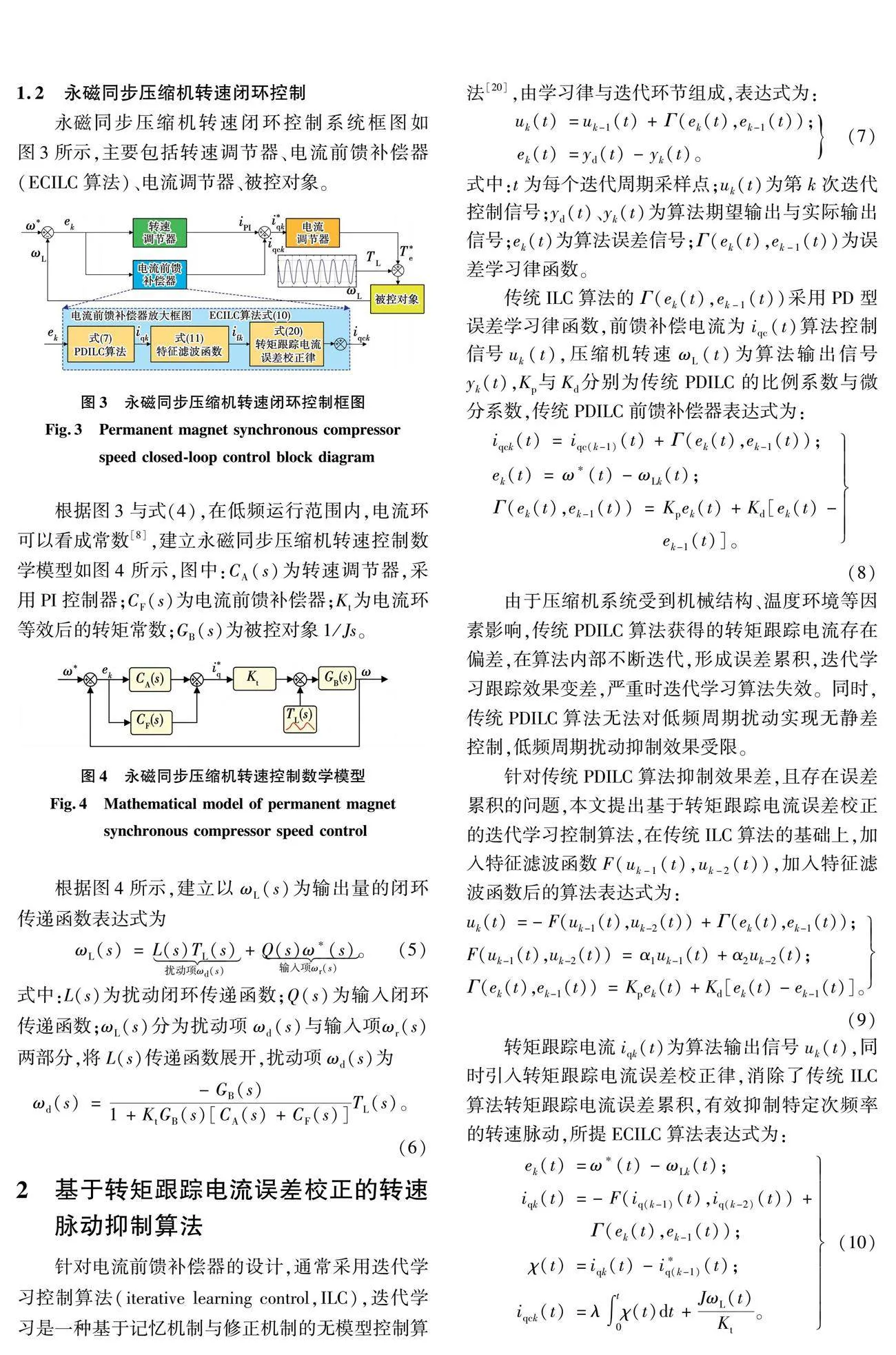
永磁同步壓縮機轉速閉環控制系統框圖如圖3所示，主要包括轉速調節器、電流前饋補償器（ECILC算法）、電流調節器、被控對象構成。

根據圖3與式（4），在低頻運行范圍內，電流環可以看成常數[8]，建立永磁同步壓縮機轉速控制數學模型如圖4所示，圖中：CA（s）為轉速調節器，采用PI控制器；CF（s）為電流前饋補償器；Kt為電流環等效后的轉矩常數；GB（s）為被控對象1 / Js。

根據圖4所示，建立以ωL（s）為輸出量的閉環傳遞函數表達式為

。 （5）

式中：L（s）為擾動閉環傳遞函數；Q（s）為輸入閉環傳遞函數。ωL（s）分為擾動項ωd（s）與輸入項ωr（s）兩部分，將L（s）傳遞函數展開，擾動項ωd（s）為

。 （6）

2 基于轉矩跟蹤電流誤差校正的轉速脈動抑制算法

針對電流前饋補償器的設計，通常采用迭代學習控制算法（iterative learning control， ILC），迭代學習是一種基于記憶機制與修正機制的無模型控制算法[20]，由學習律與迭代環節組成，表達式為：

（7）

式中：t為每個迭代周期采樣點；uk（t）為第k次迭代控制信號；yd（t）、yk（t）為算法期望輸出與實際輸出信號；ek（t）為算法誤差信號；Γ（ek（t）， ek-1（t））為誤差學習律函數。

傳統ILC算法的Γ（ek（t）， ek-1（t））采用PD型誤差學習律函數，前饋補償電流為iqc（t）算法控制信號uk（t），壓縮機轉速ωL（t）為算法輸出信號yk（t），Kp與Kd分別為傳統PDILC的比例系數與微分系數，傳統PDILC前饋補償器表達式為：

（8）

由于壓縮機系統受到機械結構、溫度環境等因素影響，傳統PDILC算法獲得的轉矩跟蹤電流存在偏差，在算法內部不斷迭代，形成誤差累積，迭代學習跟蹤效果變差，嚴重時迭代學習算法失效。同時，傳統PDILC算法無法對低頻周期擾動實現無靜差控制，低頻周期擾動抑制效果受限。

針對傳統PDILC算法抑制效果差，且存在誤差累積的問題，本文提出基于轉矩跟蹤電流誤差校正的迭代學習控制算法，在傳統ILC算法的基礎上，加入特征濾波函數F（uk-1（t）， uk-2（t）），加入特征濾波函數后的算法表達式為：

（9）

轉矩跟蹤電流iqk（t）為算法輸出信號uk（t），同時引入轉矩跟蹤電流誤差校正律，消除了傳統ILC算法轉矩跟蹤電流誤差累積，有效抑制特定次頻率的轉速脈動，所提ECILC算法表達式為：

（10）

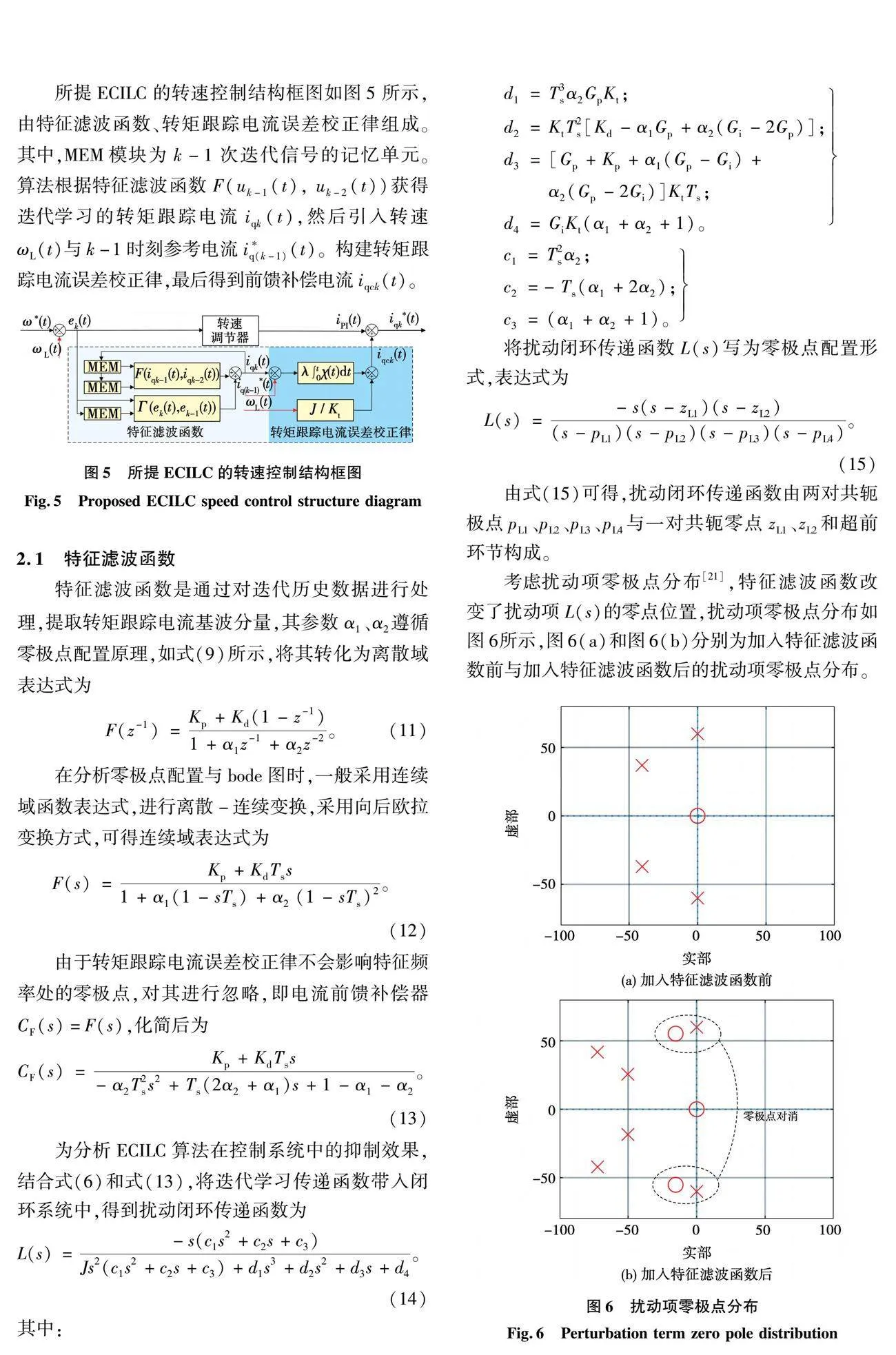
所提ECILC的轉速控制結構框圖如圖5所示，由特征濾波函數、轉矩跟蹤電流誤差校正律組成。其中，MEM模塊為k-1次迭代信號的記憶單元。算法根據特征濾波函數F（uk-1（t）， uk-2（t））獲得迭代學習的轉矩跟蹤電流iqk（t），然后引入轉速ωL（t）與k-1時刻參考電流iq（k-1）*（t）。構建轉矩跟蹤電流誤差校正律，最后得到前饋補償電流iqck（t）。

2.1 特征濾波函數

特征濾波函數是通過對迭代歷史數據進行處理，提取轉矩跟蹤電流基波分量，其參數α1、α2遵循零極點配置原理，如式（9）所示，將其轉化為離散域表達式為

。 （11）

在分析零極點配置與bode圖時，一般采用連續域函數表達式，進行離散-連續變換，采用向后歐拉變換方式，可得連續域表達式為

。 （12）

由于轉矩跟蹤電流誤差校正律不會影響特征頻率處的零極點，對其進行忽略，即電流前饋補償器CF（s）=F（s），化簡后為

。 （13）

為分析ECILC算法在控制系統中的抑制效果，結合式（6）和式（13），將迭代學習傳遞函數帶入閉環系統中，得到擾動閉環傳遞函數為

。 （14）

其中：

將擾動閉環傳遞函數L（s）寫為零極點配置形式，表達式為

。 （15）

由式（15）可得，擾動閉環傳遞函數由兩對共軛極點pL1、pL2、pL3、pL4與一對共軛零點zL1、zL2和超前環節構成。

考慮擾動項零極點分布[21]，特征濾波函數改變了擾動項L（s）的零點位置，擾動項零極點分布如圖6所示，圖6（a）和圖6（b）分別為加入特征濾波函數前與加入特征濾波函數后的擾動項零極點分布。

從圖6可以看出，加入特征濾波函數后，擾動項中的L（s）零點位置與擾動項中的TL（s）的極點位置相近，配置特征濾波函數，保證L（s）的共軛零點zL1、zL2接近TL（s）的極點位置，即可有效抑制壓縮機的轉速脈動。

根據式（14）與圖6，將c1s2+c2s+c3設計為s2+2ωcTs2s+ωs2。阻尼頻率ωc保證系統有足夠帶寬，但不能過大，否則會引起零極點位置距離過遠，TL（s）的零極點無法對消。參數α1、α2滿足：

（16）

參數α1、α2與頻率ωs、ωc關系如圖7所示。從圖中可以看出，當運行頻率ωs增大時，參數α1增大，而參數α2減小。且阻尼頻率ωc不宜取太小，否則易造成參數攝動。在運行頻率改變的工況下，需要設計自適應參數α1與α2。

（a）參數α1與頻率ωs、ωc關系 " "（b）參數α2與頻率ωs、ωc關系

圖7 "參數α1、α2與頻率ωs、ωc關系圖

Fig. 7 "Relation between α1 and α2 and ωs and ωc

2.2 轉矩跟蹤電流誤差校正律

壓縮機系統受到機械結構、溫度環境等因素的影響，傳統PDILC的轉矩跟蹤電流存在一定的偏差，且在算法中不斷迭代，形成誤差累積，嚴重時導致算法失效，針對這類型問題，提出轉矩跟蹤電流誤差校正律。

假設迭代學習誤差信號為χ（t），根據圖5可得，通過特征濾波函數F（uk-1（t）， uk-2（t）），得到的迭代學習的轉矩跟蹤電流iqk（t）與迭代學習誤差信號χ（t）、k-1時刻參考電流iq（k-1）*（t）存在以下關系：

。 （17）

負載轉矩TL（t）由兩部分組成，非周期性擾動與周期性擾動，迭代學習誤差信號累積? χ（t）dt與前饋補償電流iqck（t）構成了周期擾動項TL1（t），表達式為

（18）

式中：Kt為轉矩常數；λ為校正系數。

根據式（18）得到負載轉矩TL（t）與參考q軸電流iqk*（t）的關系，并結合電磁轉矩方程可得：

（19）

式中λ為校正系數，其取值選取小于電機運行頻率，所以轉矩跟蹤誤差校正律表達式為：

（20）

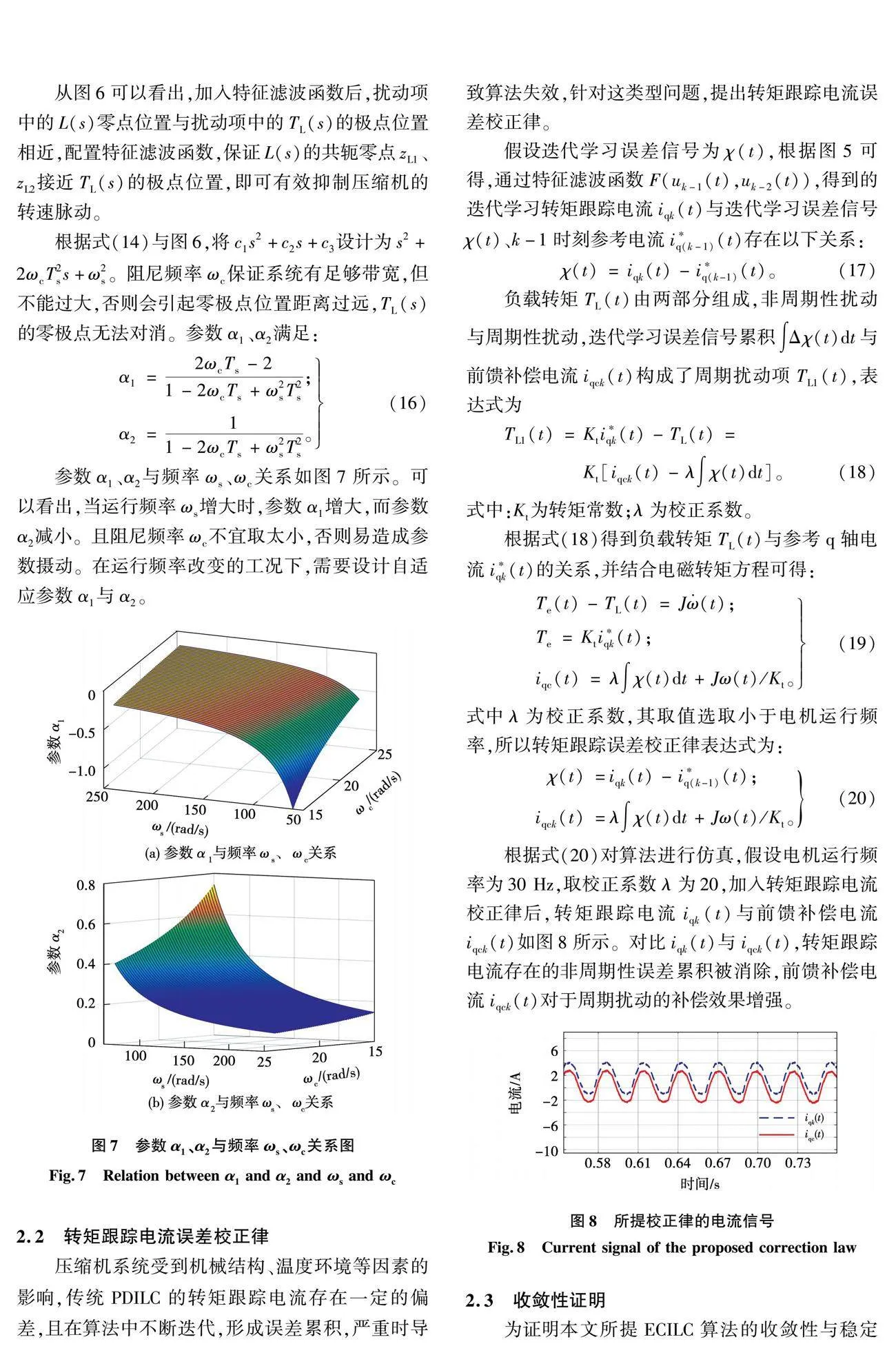
根據式（20）對算法進行仿真，假設電機運行頻率為30Hz，取校正系數λ為20，加入轉矩跟蹤電流校正律后，轉矩跟蹤電流iqk（t）與前饋補償電流iqck（t）如圖8所示。對比iqk（t）與iqck（t），轉矩跟蹤電流存在的非周期性誤差累積被消除，前饋補償電流iqck（t）對于周期擾動的補償效果增強。

2.3 收斂性證明

為證明本文所提ECILC算法的收斂性與穩定性，將式（20）的積分項進行消除，可化簡為

。 （21）

設ECILC算法的控制信號uk（t）為前饋補償電流iqck（t），狀態信號xk（t）為轉矩跟蹤電流iqk（t），轉速控制系統的輸出信號yk（t）為實際轉速信號ωL（t）。且λ取值小于電機運行頻率，所以λ?1/Ts。我們期望參考電流iqk*（t）軌跡按照轉矩補償電流iqck（t）軌跡流動，iqck（t）-iqc（k-1）（t）≈iqk*（t）-iq（k-1）*（t），結合式（10），可得

（22）

其中：

參數α1、α2的值見式（16），Δuk（t）=uk（t）-uk-1（t），由于轉矩跟蹤電流存在誤差，所以Δxk（t）gt; Δuk（t）。兩端同時取范數，可得

（23）

根據迭代學習高階學習律定理[22]，存在ρigt;0（i=0，1，…，N），使得‖αi-1 + βiKt / J‖≤ρi，且多項式z3-ρ1z2-ρ2z-ρ3的所有零點均在單位圓內，則當初態xk（t）=xd（0），則ECILC算法產生的迭代輸出一致收斂于期望軌跡。

3 實驗結果

為驗證本文提出的基于轉矩跟蹤電流誤差校正的壓縮機轉速脈動抑制算法策略的有效性，搭建壓縮機測試平臺如圖9所示，并進行實驗驗證。在該平臺上對傳統PDILC算法與本文提出的ECILC算法進行實驗對比，實驗壓縮機用PMSM控制系統參數如表1所示，采用DSP芯片TMS320F28335作為控制器，其開關頻率為10kHz，電流環執行周期為100μs，轉速執行周期為1ms。

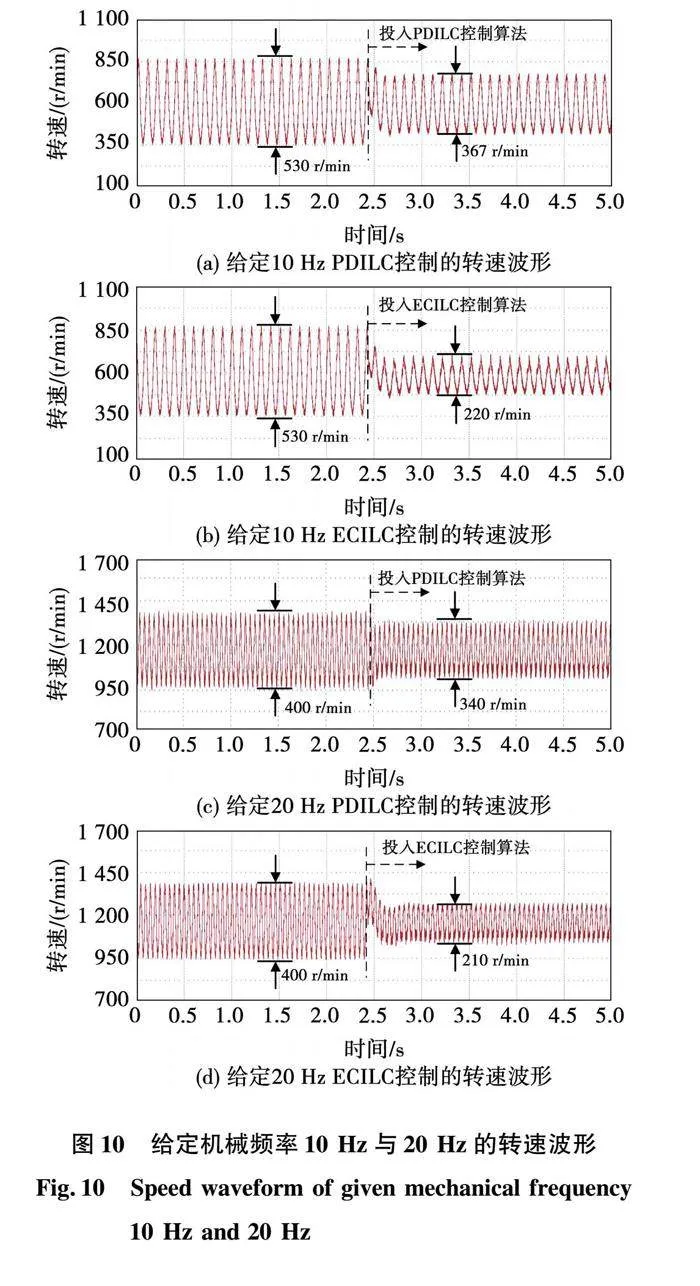
給定機械頻率10Hz與20Hz下，傳統PDILC控制和所提ECILC控制的轉速波形如圖10所示。可以看出，在10Hz下，傳統PDILC控制算法將轉速脈動峰峰值從530r/min抑制到367r/min，而所提ECILC控制算法可以抑制到220r/min。在20Hz下，傳統PDILC將轉速脈動峰峰值從400r/min抑制到340r/min，而所提ECILC控制算法可以抑制到210r/min。與傳統PDILC控制算法相比，所提ECILC控制算法的轉速脈動抑制效果更顯著。

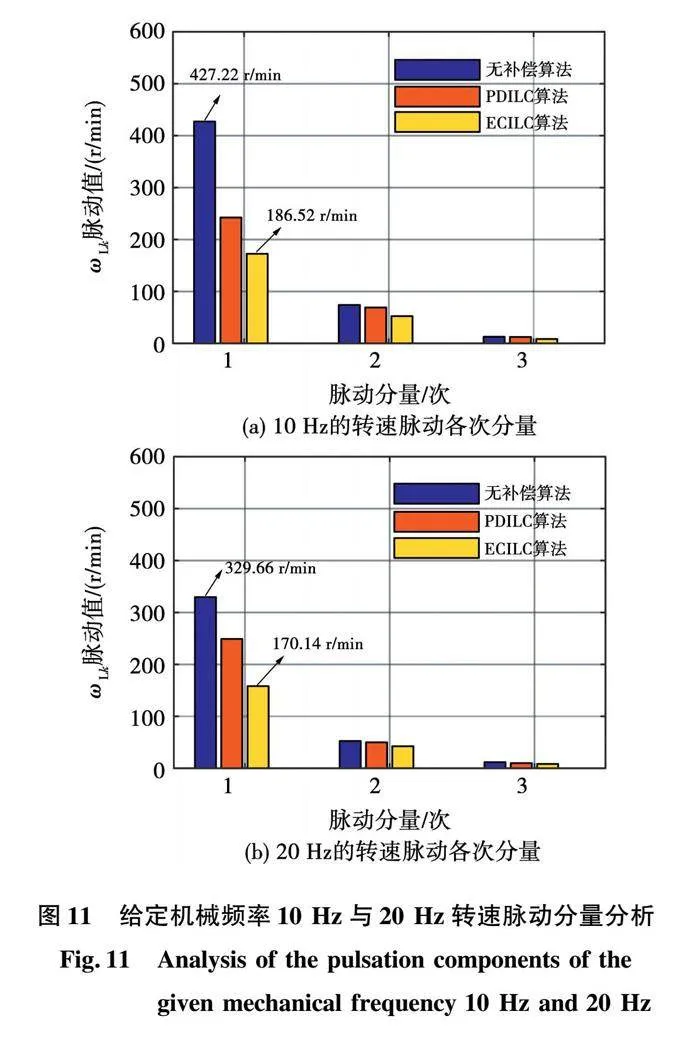
給定機械頻率10Hz與20Hz轉速脈動分量分析如圖11所示。圖11（a）和圖11（b）分別為給定機械頻率10Hz和20Hz的轉速脈動各次分量。從圖11可以看出，所提ECILC控制算法的轉速脈動基波分量分別為186.52r/min（給定10Hz）和170.14r/min（給定20Hz），比傳統PDILC控制算法的轉速基波分量少，且相較于無補償算法可以抑制1/3左右，而對于其他次脈動分量，所提ECILC算法抑制效果一般，說明所提ECILC控制算法主要是通過抑制轉速基波分量，來抑制壓縮機轉速脈動。

給定機械頻率20Hz ECILC控制的交軸電流跟蹤效果如圖12所示。從圖中可以看出，實際交軸電流iq按照參考交軸電流iq*軌跡進行實時跟蹤，且在加入ECILC控制算法后，相當于注入電流諧波，實際交軸電流的iq諧波含量增加，所以本文所提的ECILC控制算法會導致電機部分銅耗增加。

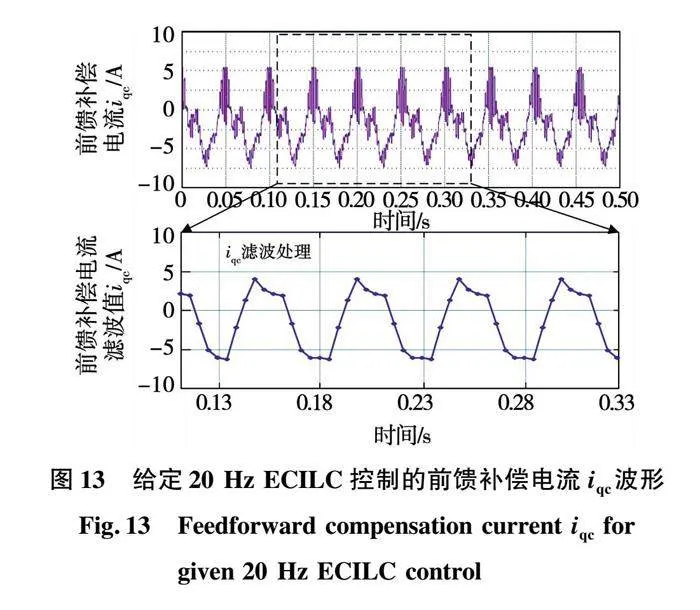
給定機械頻率20Hz ECILC控制的前饋補償電流iqc波形如圖13所示。從圖中可以看出，在加入所提的ECILC算法后，前饋補償電流中存在高頻次諧波分量。將前饋補償電流iqc進行采樣濾波處理，其波形與圖1（b）所示的壓縮機負載轉矩曲線類似，證明前饋補償電流可以跟蹤壓縮機負載轉矩，從而抑制壓縮機的轉速脈動。

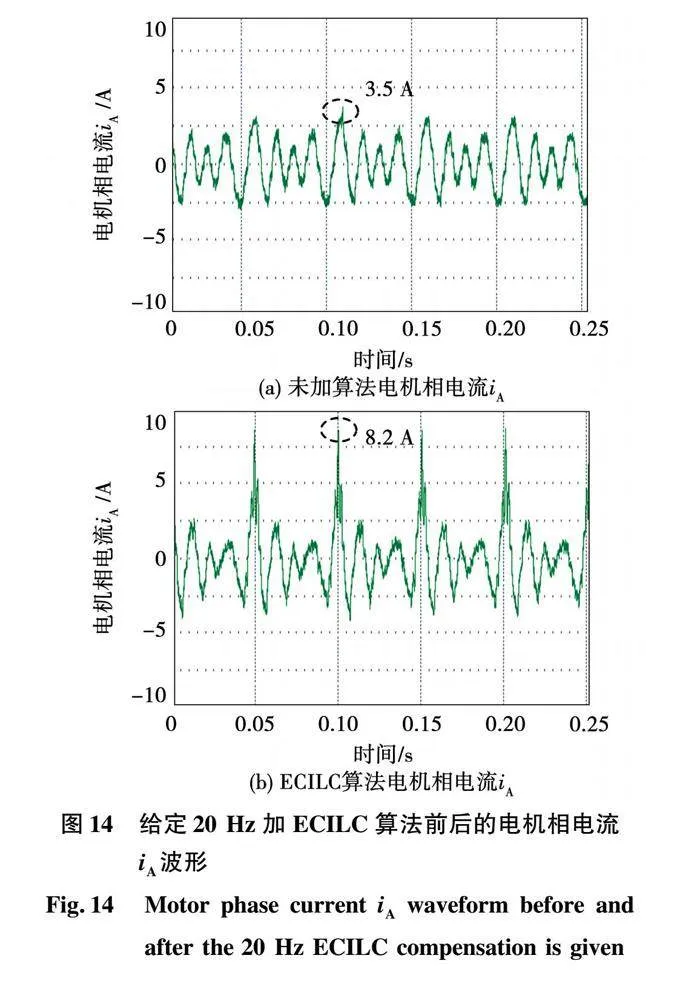
給定20Hz加ECILC算法前后的電機相電流iA波形如圖14所示，從圖中可以看出，加ECILC算法后，電機相電流中存在高頻次諧波分量。未加轉速脈動抑制算法與加ECILC算法相比，其相電流iA最大振幅值增大4.7A，主要原因是由單轉子壓縮機負載轉矩峰值引起的，說明ECILC控制算法可以有效抑制壓縮機負載轉矩峰值，從而抑制壓縮機的轉速脈動。

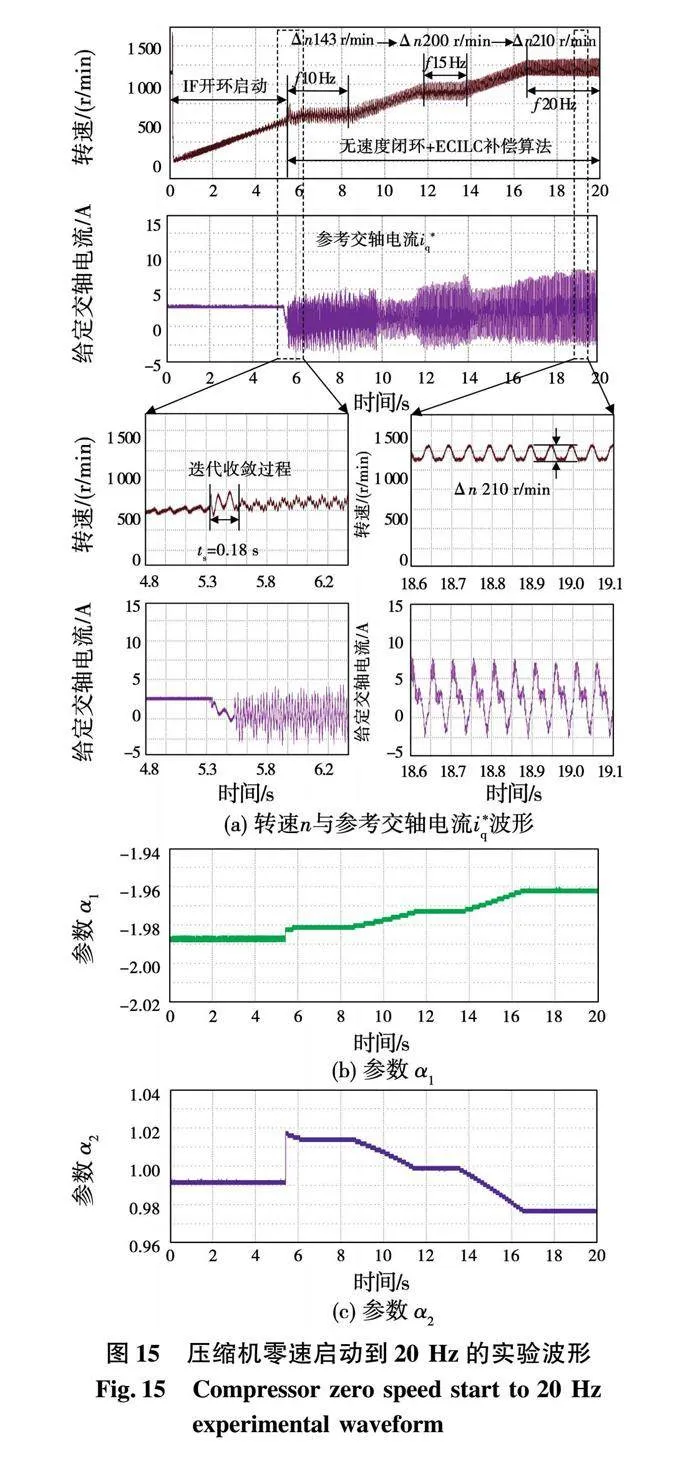
壓縮機零速啟動到20Hz的實驗波形如圖15所示，其中，圖15（a）～圖15（c）分別為轉速n與參考電流iq*波形、參數α1、參數α2。運行頻率按照0到10Hz到15Hz再到20Hz變化。從0到10Hz采用電流頻比控制，即IF開環啟動，在10Hz后投入無速度閉環算法與ECILC補償算法。從圖15可以看出，所提ECILC算法的轉速脈動峰峰值在250r/min以下（10～20Hz），與圖10未加轉速脈動抑制算法時轉速脈動峰峰值在530r/min（10Hz）、400r/min（20Hz）相比，轉速脈動抑制效果顯著；且算法在0.18s后可以快速收斂；同時，參數α1與α2適應運行頻率fs變化，證明所提ECILC控制算法動態過程中具有良好的轉速脈動抑制效果。

為進一步評估算法在低頻運行頻率范圍內的轉速脈動抑制效果，定義轉速脈動抑制率，表達式為

。 （24）

式中 、 為無抑制算法、有抑制算法的轉速紋波極差。轉速脈動抑制率越低，轉速脈動抑制效果越好。

給定10～30Hz兩種算法轉速脈動抑制率對比如圖16所示。從圖中不難看出，在整個低頻運行頻率范圍內，所提的ECILC控制算法的轉速脈動抑制率始終低于傳統PDILC控制算法，ECILC抑制效果顯著，但是隨著壓縮機運行頻率的升高，兩種控制方法的轉速脈動抑制率也升高，這主要原因是由于高頻運行受到轉動慣量的影響較小，導致轉速脈動較小，抑制效果變差。

4 結 "論

本文以抑制壓縮機低頻轉速脈動為目標，研究了一種基于轉矩跟蹤電流誤差校正的壓縮機轉速脈動抑制算法。通過與傳統迭代學習轉速脈動抑制算法進行理論分析、實驗對比，得出如下結論：

1）本文所提的轉速脈動抑制算法引入特征濾波函數，用來提取轉矩電流基波分量，與傳統迭代學習轉速脈動抑制算法相比，壓縮機在特定次頻率處的轉速脈動抑制效果更顯著。

2）在引入特征濾波函數的基礎上，提出轉矩跟蹤電流誤差校正律，對轉矩跟蹤電流與參考交軸電流的誤差進行校正，消除了傳統迭代學習轉矩跟蹤電流存在的誤差累積，算法跟蹤性能好。

3）實驗結果證明采用本文所提的轉速脈動抑制算法在低頻運行過程中參數可以實現自適應變化，無需查表離線補償，且轉速脈動抑制效果顯著，算法穩定性好。

參 考 文 獻：

[1] 張曉軍，楊家強，楊昊林. 一種基于永磁同步電機繞組銅耗功率最大的電動汽車母線電容放電方法[J]. 中國電機工程學報，2022，42（17）： 6460.

ZHANG Xiaojun，YANG Jiaqiang，YANG Haolin，et al．A DC-bus capacitor discharge method based on maximum copper consumption power of permanent magnet synchronous motor windings in electric vehicles [J]．Proceedings of the CSEE，2022，42（17）： 6460.

[2] 蘭志勇，李延昊，羅杰，等.一種自適應擴展卡爾曼濾波的永磁同步電機無位置傳感器矢量控制[J].電機與控制報，2024，28（3）： 141.

LAN Zhiyong，LI Yanhao，LUO Jie，et al．Sensorless vector control of permanent magnet synchronous motor based on adaptive extended Kalman filter [J]．Electric Machines and Control，2024，28（3）： 141．

[3] 黃萬奔，楊家強，鄧鎔峰，等．高功率因數無電解電容永磁電機變頻系統逆變器電流控制策略[J]．電機與控制學報，2022，26（8）： 1．

HUANG Wanben，YANG Jiaqiang，DENG Rongfeng，et al．Inverter current control strategy for high power factor electrolytic capacitor-less permanent magnet motor drive system[J]．Electric Machines and Control，2022，26（8）： 1．

[4] ZHAO N，WANG G，LI B，et al．Beat phenomenon suppression for reduced DC-link capacitance IPMSM drives with fluctuated load torque[J]．IEEE Transactions on Industrial Electronics，2018，66（11）： 8334．

[5] 宋守許，李諾楠，杜毅等．抑制永磁同步電機轉速脈動的轉子再設計方法[J]．中國機械工程，2019，30（17）： 2084．

SONG Shouxu，LI Nuonan，DU Yi，et al．Rotor redesign method for suppressing torque ripples of permanent magnet synchronous motors[J].China Mechanical Engineering，2019，30（17）： 2084．

[6] 韓雪巖，劉文彬，朱龍飛.基于自抗擾的永磁同步電機附加諧波損耗抑制方法[J].電機與控制學報，2024，28（2）： 87.

HAN Xueyan，LIU Wenbin，ZHU Longfei．Suppression method of additional harmonic loss of permanent magnet synchronous motor based on active disturbance rejection technology [J]．Electric Machines and Control，2024，28（2）： 87．

[7] 陳哲，張序軒，劉春強，等. 基于比例諧振型自抗擾控制的永磁同步電機電流解耦及諧波抑制策略研究[J]. 中國電機工程學報，2022，42（24）： 9062.

CHEN Zhe，ZHANG Xuxuan，LIU Chunqiang，et al．Research on current decoupling and harmonic suppression strategy of permanent magnet synchronous motor based on proportional resonance type ADRC [J]．Proceedings of the CSEE，2022，42（24）： 9062．

[8] HUO J，ZHAO N，GAO R，et al．Torque ripple compensation with anti-overvoltage for electrolytic capacitorless PMSM compressor drives[J]．IEEE Journal of Emerging and Selected Topics in Power Electronics，2022，10（5）： 6148．

[9] WANG S，ZHANG G，WANG Q，et al．Torque disturbance compensation method based on adaptive fourier-transform for permanent magnet compressor drives[J]．IEEE Transactions on Power Electronics，2022，38（3）： 3612．

[10] LI M，XIAO H，CHENG M，et al．An adaptive strategy based on repetitive predictive control for improving adaptability of LCL-type grid-connected inverters under weak grid[J]．IEEE Transactions on Power Electronics，2022，37（3）： 2562.

[11] ELIOMAR R C D ， LUNARDI A ， FILHO A J S . Current control for DFIG systems under distorted voltage using predictive–repetitive control[J]．IEEE Journal of Emerging and Selected Topics in Power Electronics， 2021，9（4）： 4354．

[12] 張巧芬，劉彥呈，郭昊昊，等. 用于永磁同步電機周期性轉速脈動抑制的重復控制[J]. 控制理論與應用，2022，39（3）： 432.

ZHANG Qiaofen，LIU Yancheng，GUO Haohao，et al．Repetitive control for periodic speed ripples suppression of permanent magnet synchronous motor [J]．Control Theory and Applications，2022，39（3）： 432．

[13] 付興賀，顧勝東，何航，等. 基于新型串聯內模擴張狀態觀測器的PMSM齒槽轉矩補償控制方法[J]. 中國電機工程學報，2022，42（23）： 8729.

FU Xinghe，GU Shengdong，HE Hang，et al．Compensation and rejection of cogging torque of PMSM based on novel internal model observer in series with extended state observer [J]．Proceedings of the CSEE，2022，42（23）： 8729．

[14] 仲宇翔，林鶴云，王激堯，等. 基于滑模控制的記憶電機調磁轉速波動抑制[J]. 中國電機工程學報，2023，43（7）： 2512.

ZHONG Yuxiang，LIN Heyun，WANG Jiyao，et al．Speed variation suppression for memory machine during magnetization state manipulation based on sliding mode control[J]．Proceedings of the CSEE，2023，43（7）： 2512．

[15] 卜飛飛，郭子韜，顧毅君，等. 基于改進型降階觀測器的永磁直驅伺服電動機轉矩擾動抑制策略[J]. 電工技術學報，2022，37（16）： 4104.

BU Feifei，GUO Zitao，GU Yijun，et al．Torque disturbance suppression strategy of permanent magnet direct drive servo motor based on improved reduced order observer [J]. Transactions of China Electrotechnical Society，2022，37（16）： 4104．

[16] WANG Y，GAO Y，ZHAO C，et al．Iterative learning based torque ripple suppression of flux-modulation double-stator machine[J]．IEEE Transactions on Industrial Electronics，2021，69（7）： 6645．

[17] BI G，ZHANG G，WANG G，et al．Adaptive iterative learning control-based rotor position harmonic error suppression method for sensorless PMSM drives[J]．IEEE Transactions on Industrial Electronics，2021，69（11）： 10870．

[18] HUANG M，DENG Y，LI H，et al．Torque ripple suppression of PMSM using fractional-order vector resonant and robust internal model control[J]．IEEE Transactions on Transportation Electrification，2021，7（3）： 1437．

[19] 曹榮敏，鄭鑫鑫，侯忠生. 基于改進多入多出無模型自適應控制的二維直線電機迭代學習控制[J]. 電工技術學報，2021，36（19）： 4025.

CAO Rongmin，ZHENG Xinxin，HOU Zhongsheng．An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-Dimensional linear motor[J]．Transactions of China Electrotechnical Society，2021，36（19）： 4025．

[20] 哀薇，胡林威，李向陽，等.基于自抗擾迭代學習控制的開關磁阻電機轉矩脈動抑制[J].控制理論與應用，2020，37（10）： 2098.

AI Wei，HU Linwei，LI Xiangyang，et al．Active disturbance rejection based iterative learning control for torque ripple suppression in switched reluctance motor [J]．Control Theory and Applications，2020，37（10）： 2098.

[21] 孫燦．基于氮化鎵功率器件的高速永磁同步電機驅動系統若干關鍵技術研究[D]．杭州：浙江大學，2022.

[22] AI Q，KE D，ZUO J，et al. High-order model-free adaptive iterative learning control of pneumatic artificial muscle with enhanced convergence[J]．IEEE Transactions on Industrial Electronics，2020，67（11）： 9548.

（編輯：邱赫男）