螺桿機用并軸雙轉子永磁電機齒槽力矩機理分析與抑制

摘 "要：針對并軸雙轉子永磁電機過大的齒槽力矩以及轉矩脈動大等電磁問題，采用傳統單個槽齒槽轉矩理論以及雙轉子電機邊端力矩波動理論進行分析，計算了并軸雙轉子電機齒槽力矩的特殊組成成分以及其各部分轉矩的諧波階次。分析改變磁極偏心距和轉子斜極對電機齒槽力矩和轉矩特性的影響。采用響應面法構建電機的多目標優化模型，通過改變永磁體偏心距和斜極塊數來約束電機的優化變量，并采取約束關系以及優化目標求解出最優轉子結構參數。構建有限元模型，驗證齒槽力矩理論的正確性。對比采用最優轉子結構參數下電機的電磁性能與優化前電機的電磁性能，優化后電機的齒槽力矩、轉矩脈動等電磁性能進一步提升，驗證了采用磁極偏心和轉子斜極復合結構的有效性。

關鍵詞：并軸雙轉子永磁電機；齒槽力矩；轉子斜極；響應面

DOI：（編輯填寫）

中圖分類號：TM351 " " " " " "文獻標志碼：A " " " " "文章編號：（編輯填寫）

Mechanism analysis and suppression of cogging torque in parallel axis dual rotor permanent magnet motors for screw machines

GE Baojun， SHANG Haiyang， LIN Peng

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080， China）

Abstract： In view of the electromagnetic problems such as excessive cogging moment and large torque pulsation of the parallel shaft dual-rotor permanent magnet motor， the traditional theory of single-slot cogging moment and the theory of fluctuation of side-end torque of the dual-rotor motor are analyzed， and the special components of the cogging moment of the parallel shaft dual-rotor motor as well as the harmonic orders of the torque of each part of the cogging moment are calculated. The effects of changing the pole eccentricity and rotor inclined pole on the cogging moment and torque characteristics of the motor are analyzed. The response surface method is used to construct a multi-objective optimization model of the motor， and the optimization variables of the motor are constrained by changing the permanent magnet eccentricity and the number of inclined pole blocks， and the optimal rotor structure parameters are solved through the constraint relationship as well as the optimization objectives. The finite element model is constructed to verify the correctness of the cogging moment theory. Comparing the electromagnetic performance of the motor under the optimal rotor structure parameters with that of the motor before optimization， the electromagnetic performance of the motor after optimization， such as cogging moment and torque pulsation， is further improved， which verifies the validity of adopting the composite structure of pole eccentricity and rotor inclined pole.

Keywords： parallel axis dual rotor permanent magnet motor; cogging torque; rotor oblique pole; response surface

0 引 "言

與傳統的螺桿泵類機械驅動裝置相比，并軸雙轉子永磁電機去除了傳動齒輪，將兩臺完全相同的永磁電機同時削去一部分定子繞組和定子鐵心，然后將兩部分定子合二為一，組成1種近似橢圓型的新型定子結構。同時2個轉子直接接觸，達到同步對轉的效果，從而用來直接驅動螺桿泵類機械裝置的2個軸，這樣使得該類裝置的一體性更好。但由于定子的缺失，使得該類電機轉矩波動較大，究其原因主要是由于并軸雙轉子永磁電機定子繞組的缺失，從而邊端繞組產生比較大的邊端力，加上非削去部分的齒槽轉矩從而形成并軸雙轉子永磁電機特殊的齒槽力矩。抑制齒槽力矩是并軸雙轉子永磁電機能夠穩定運行的基礎，所以本文通過參考傳統旋轉電機的齒槽轉矩的優化方法，通過改變磁極偏心距與轉子斜極的復合轉子結構來對螺桿機用并軸雙轉子永磁電機的齒槽力矩進行抑制。

對于齒槽轉矩的削弱，各國學者做了大量的研究工作，傳統電機轉子永磁體和定子齒共同作用從而產生齒槽轉矩。文獻[1-3]研究了槽口寬以及極槽配合對齒槽轉矩波動的影響，槽開口寬越小齒槽轉矩抑制效果越好；文獻[4-5]研究結果表明轉子斜極對齒槽轉矩的抑制效果十分明顯；文獻[6-7]通過改變永磁體偏心距的方法來調節氣隙磁密分布，使氣隙磁密波形更加接近正弦，從而使得電機的齒槽轉矩波動大大降低；文獻[8]總結出4種削弱齒槽轉矩的方法：極弧系數優化、極槽配合優化、斜極優化以及槽開口優化。

直線永磁電機里空載轉矩不同于傳統電機，其空載轉矩包括兩部分：一個是定子開槽和動子永磁體產生的齒槽轉矩，另一個是由于定子鐵心不連續存在邊端所產生的邊端力矩。大多數研究者認為，直線永磁電機空載力波動主要由邊端力組成，直線電機同傳統電機相同，過大的轉矩波動是不理想的，所以有大量的學者針對直線電機特有的邊端力矩進行優化。文獻[9]中為了解決弧形永磁電機過大的邊端力矩，借鑒傳統電機中改變單個定子的角度和定子之間配合從而對邊端力波動進行削弱；文獻[10]中戶恒在博士通過改變永磁體偏心距和優化定子角度將弧形永磁電機的邊端力矩波動進行了十分有效地抑制。文獻[11-12]通過定子鐵心齒部開槽的方法成功削弱邊端力波動；文獻[13]提出可以通過優化定子長度和定子邊端形狀來優化邊端力波動；文獻[14-15] 通過調整直線電機定子齒距從而有效地削弱了邊端力波動。已經有大量的學者針對直線永磁電機空載力矩的抑制上提出很多方法。同時，在并軸雙轉子永磁電機領域，由于定子鐵心和繞組的缺失，同樣會產生同直線電機一樣的邊端力波動。文獻[16]戴思銳博士提出一種并行直驅連體定子永磁電機并且對電機的電磁性能進行了研究。哈爾濱理工大學陶大軍教授[17]提出一種雙并列永磁電機，對其不平衡電磁力進行了深入計算。以上兩位對并軸雙轉子永磁電機的分析主要停留在提出該類型電機與電機電磁設計和性能分析上，針對并軸雙轉子永磁電機的齒槽力矩分析上仍處于空白階段，由于并軸雙轉子永磁電機設計思路來自于直線永磁電機，因此并軸雙轉子永磁電機齒槽力矩分析可以參考直線永磁電機齒槽力矩的分析。

本文從單體電機出發，設計了一臺72槽16極的并軸雙轉子永磁電機，其中電機左右兩側的極數和槽數分別為8和36。由于并軸雙轉子永磁電機左右兩部分完全相同，所以為了簡化分析過程，只考慮單側定轉子即可，也就是36槽8極的電機部分。通過理論論證單側邊端繞組所產生的邊端力諧波階次，利用有限元進行仿真驗證，從而找出并軸雙轉子永磁電機齒槽力矩大的原因。最后采用復合轉子結構的削弱方法對電機的特殊齒槽力矩進行優化，使并軸雙轉子永磁電機電磁特性更加接近傳統結構電機。

1.1 并軸雙轉子永磁電機結構示意圖

本文所采用的并軸雙轉子永磁電機主要由傳統單體電機削去1/4定子鐵心和定子繞組設計而來。根據定子分塊原則，在設計雙轉子驅動電機時，為了保持削去一部分定子之后，剩余的定子與永磁體依舊能形成單元電機，保證雙轉子電機的磁場三相對稱，因此選擇削去1/4定子鐵心，并且將2個削去定子鐵心后的電機合二為一，對2個削去后定子鐵心空白部分進行填充，形成一種近似橢圓形定子。并且2個轉子相互靠近，中間留有氣隙，永磁體磁極相異排布，最終形成并軸雙轉子永磁電機，該電機的結構示意圖如圖1所示，其結構參數如表1所示。圖2為傳統單體電機削去和非削去兩部分。

由于定子繞組的缺失，電機內部磁場改變，電機的各項電磁性能就會發生變化，會產生比較大的齒槽力矩和輸出轉矩波動。本文將對該電機的齒槽力矩進行了理論分析，并且進一步優化了電機的電磁性能。

2 傳統單體電機齒槽轉矩理論分析

2.1 傳統電機齒槽轉矩理論分析

并軸雙轉子電機雖然削去了一部分定子鐵心，但其設計來源依舊是傳統單定子單轉子電機，由于傳統電機定子開槽的緣故，定子齒和永磁體相互作用產生齒槽力矩。同樣并軸雙轉子電機仍然保留了大部分的定子齒，所以其空載轉矩中仍然含有齒槽力矩。這里為了方便的計算出雙轉子電機的齒槽力矩，采用單個槽產生的齒槽轉矩理論展開推導，將雙轉子電機不連續的定子槽以單個槽為單位劃分，計算單個槽產生的轉矩波動，再將單個槽所產生的轉矩波動進行疊加，從而得到所有槽產生的轉矩。其中單個槽產生的轉矩波動用傅里葉形式分解[18]為

（1）

式中：Tst為單個槽產生的齒槽轉矩；Ti為第i次諧波齒槽轉矩幅值；p為電機極對數；θ為轉子轉過的機械角度。

計算出單個槽所產生的轉矩后，電機中單個槽通過調整相位可以得到不同位置的槽。所以單個槽通過調整相位后可以得到電機里Ns個槽產生的合成齒槽轉矩可以表示為 " " " " " " "（2）

式中：Tcog為電機的合成齒槽轉矩；k為第k個槽。分析式（2），式中sin（2pπi）恒等于0，所以只有當上式的分母為0時，此諧波項不為0，因此可得：

（3）

式中：Nc為電機槽數和電機極數的最小公倍數；C為任意整數。

式（1）為采用單個槽所產生的齒槽轉矩理論計算公式，此時單個槽產生的齒槽轉矩諧波階次主要為2p的倍數。在傳統電機中，不同相位決定了槽與槽的位置，當以一個完整電機為周期時，通過計算單個槽所產生的齒槽轉矩從而相互疊加，可以得到合成齒槽轉矩如式（3）所示，從而總的合成齒槽轉矩的諧波次數等于電機槽數Ns和電機極數2p的最小公倍數Nc。通過以上的分析，電機單個槽會產生較大的低階齒槽轉矩，但在電機設計過程中，可以通過合理的極槽配合，從而將低階齒槽轉矩諧波進行削弱。所以盡可能的增大槽數和極數的最小公倍數，來得到較小的齒槽轉矩諧波幅值。

以8極48槽傳統圓形電機為例，將2p=8代入式（1）中，可得8極48槽電機里單個槽產生的齒槽轉矩為

（4）

將2p=8、Ns=48代入式（3）中，可得到8極48槽電機的合成齒槽轉矩為

（5）

式（4）中求得的為48槽8極傳統圓形電機里單個槽所產生的齒槽轉矩諧波，其齒槽轉矩諧波階次主要為8及8的倍數；式（5）中為48槽8極傳統圓形電機合成齒槽轉矩，其諧波階次主要為48及48的倍數。對比兩式可知，由單個槽產生的低階次諧波可以通過合理的極槽配合相互抵消，從而可以有效地削弱電機里的齒槽轉矩波動。

3 并軸雙轉子永磁電機特殊齒槽力矩分析

通過借鑒傳統單個槽所產生的齒槽轉矩理論方法，本節將對并軸雙轉子永磁電機非削去部分所產生的常規齒槽轉矩Fslot以及削去部分邊端槽所產生的邊端力Fend進行理論分析，兩部分相互疊加共同組成了并軸雙轉子永磁電機的特殊齒槽力矩，并且通過有限元進行了仿真驗證。

3.1 并軸雙轉子永磁電機邊端力分析

在并軸雙轉子永磁電機里，由于削去了部分定子鐵心和定子繞組，那么在電機非削去定子部分會存在2個邊端槽，該邊端槽分別與轉子永磁體發生作用產生邊端力，將并軸雙轉子永磁電機的削去和非削去部分分別沿軸向展開，即可得到兩部分電機如圖3所示，圖中Fslot和Fend分別表示齒槽力和邊端力。

將單邊并軸雙轉子永磁電機順時針旋轉90°，如上圖3（b）所示，左、右邊端繞組分別和轉子永磁體作用產生邊端力。左、右邊端力以傅里葉形式可以表示[19-20]為：

（6）

式中：FL（x）為左邊端力；FR（x）為右邊端力；F0為端力的直流分量；Fn為端力的n次諧波幅值；τp為轉子極距；δ為左邊端力和右邊端力的相位差。

所以整個合成邊端力為

（7）

式中FW為整個電機受的邊端力合力。

式（7）為單邊并軸雙轉子永磁電機里合成的邊端力，本文的并軸雙轉子電機在設計初期定子部分已經確定，因此后文采用復合轉子結構對齒槽力矩進行優化。

接下來對并軸雙轉子永磁電機削去和非削去部分的電機邊端所產生的齒槽力矩的諧波階次進行分析，研究對象分別為：單邊36槽6極并軸雙轉子電機以及削去部分12槽2極電機。將2p=6，Ns=36代入到式（1）中，可以得到非削去部分電機邊端繞組所產生的齒槽轉矩為

（8）

將2p =2，Ns =12代入到式（1）中可以得到削去部分電機邊端繞組所產生的齒槽轉矩為

（9）

根據以上的分析可知，36槽6極電機的齒槽轉矩6及6的倍數次諧波主要由邊端繞組所產生，若該電機為傳統電機，則該齒槽轉矩的該次諧波將會被下一個槽所抵消，最后只剩下48及48的倍數次諧波，但由于該電機部分繞組的丟失，所以缺少了與之作用的6及6的倍數次諧波，因此并軸雙轉子永磁電機非削去部分邊端繞組會存在6及6的倍數次諧波；同理對于削去2p =2，12槽電機部分來說，會產生2及2的倍數次諧波，并且由于兩部分電機由單個電機分割而來，所以非削去部分的邊端繞組依舊會產生與削去部分邊端繞組所疊加的2及2的倍數次諧波，因此非削去部分的電機邊端會產生低階的偶數次諧波，該次諧波主要形成了并軸雙轉子永磁電機的邊端力，加上非削去部分的齒槽轉矩即單體電機分割前所存在的齒槽轉矩共同形成了并軸雙轉子永磁電機的特殊齒槽力矩。

3.2 有限元仿真驗證

經過對單邊8極36槽的并軸雙轉子永磁電機力矩波動的理論分析，能夠得出：非削去部分繞組槽除邊端繞組槽以外產生的齒槽力矩主要為傳統電機里的齒槽轉矩Fslot，也就是雙轉子電機由于定子開槽所產生的齒槽轉矩。同時雙轉子電機定子部分存在邊端，該部分定子鐵心與永磁體相互作用從而產生邊端力矩。定子繞組槽的缺失，該次諧波無法被抵消，從而形成了并軸雙轉子永磁電機的齒槽力矩。通過有限元分析，對照48槽8極傳統圓形電機和單邊36槽8極并軸雙轉子永磁電機的齒槽力矩，從而驗證上述分析。其中2個電機其余尺寸均保持一致。

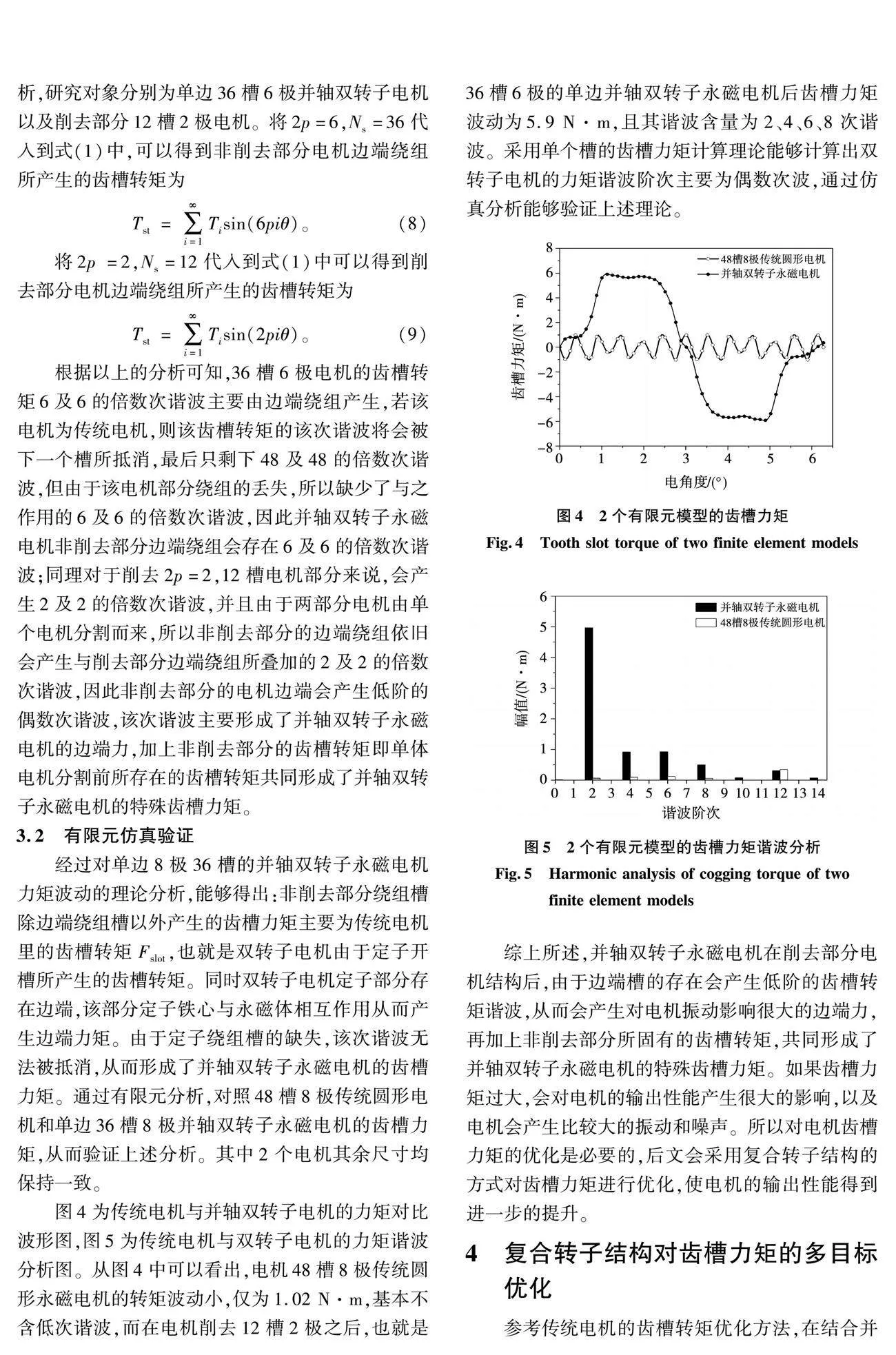
圖4為傳統電機與并軸雙轉子電機的力矩對比波形圖，圖5為傳統電機與雙轉子電機的力矩諧波分析圖。從圖4中可以看出，電機48槽8極傳統圓形永磁電機的轉矩波動小，僅為1.02 N·m，基本不含低次諧波，而在電機削去12槽2極之后，也就是36槽6極的單邊并軸雙轉子永磁電機后齒槽力矩波動為5.9 N·m，且其諧波含量為2、4、6、8次諧波。采用單個槽的齒槽力矩計算理論能夠計算出雙轉子電機的力矩諧波階次主要為偶數次波，通過仿真分析能夠驗證上述理論。

綜上所述，并軸雙轉子永磁電機在削去部分電機結構后，由于邊端槽的存在會產生低階的齒槽轉矩諧波，從而會產生對電機振動影響很大的邊端力，再加上非削去部分所固有的齒槽轉矩，共同形成了并軸雙轉子永磁電機的特殊齒槽力矩。如果齒槽力矩過大，會對電機的輸出性能產生很大的影響，以及電機會產生比較大的振動和噪聲。所以對電機齒槽力矩的優化是必要的，后文會采用復合轉子結構的方式對齒槽力矩進行優化，使電機的輸出性能得到進一步的提升。

4 復合轉子結構對齒槽力矩的多目標優化

參考傳統電機的齒槽轉矩優化方法，在結合并軸雙轉子永磁電機的特殊結構，本文通過改變電機的永磁體偏心距與轉子斜極對其特殊的齒槽力矩進行優化。

4.1 磁極偏心對齒槽力矩的影響

通過改變并軸雙轉子永磁電機磁極的偏心距[21]，優化氣隙磁場，優化電機的整體性能，圖6給出了并軸雙轉子永磁電機耦合區以及磁極偏心結幾何示意圖，Ri為永磁體內半徑，R0為永磁體外半徑，hd為永磁體端部厚度，hm為永磁體中間厚度，θ0為永磁體端部與永磁體d軸之間的夾角。在確定氣隙最小長度前提下，根據幾何關系給出了不同永磁體端部厚度與偏心距的數學表達式為

（10）

在ΔMNO中，可以求得MN的長度為

（11）

式中：Rs為定子內徑；g為氣隙最小長度。因此，α為

（12）

式中：θ0=παp/（2p）；p為極對數；αP為極弧系數。同理，在ΔOO’E中，可以求得磁極外半徑R0為

（13）

因此可以得到偏心距離γ為

（14）

圖7為齒槽力矩隨偏心距變化曲線。

從圖7可以看出改變永磁體的偏心距對電機齒槽力矩的影響非常顯著，其中齒槽力矩下最小的偏心距為24 mm，較不偏心下的齒槽力矩降低了70%，但不能一味的追求齒槽力矩的下降，還要關注電機的其他電磁性能，因此后文會采用復合轉子結構則優選擇偏心距。

4.2 轉子斜極對齒槽力矩的影響

由于螺桿機用并軸雙轉子永磁電機結構特殊，兩個轉子互相為彼此提供由定子缺失所失去的電磁力，但效果并不能媲美完整電機。所以一方面為了降低電機特殊的齒槽力矩，另一方面為了電機的轉子受力盡量均勻，從而選擇轉子斜極的方法。這樣不僅可以優化電機的齒槽力矩，還可以將永磁體沿轉子的軸向分段并且錯開合適的角度，使得轉子所受到的磁拉力可以更加均勻的分布在轉子上，盡量讓電機運行的更加平穩。

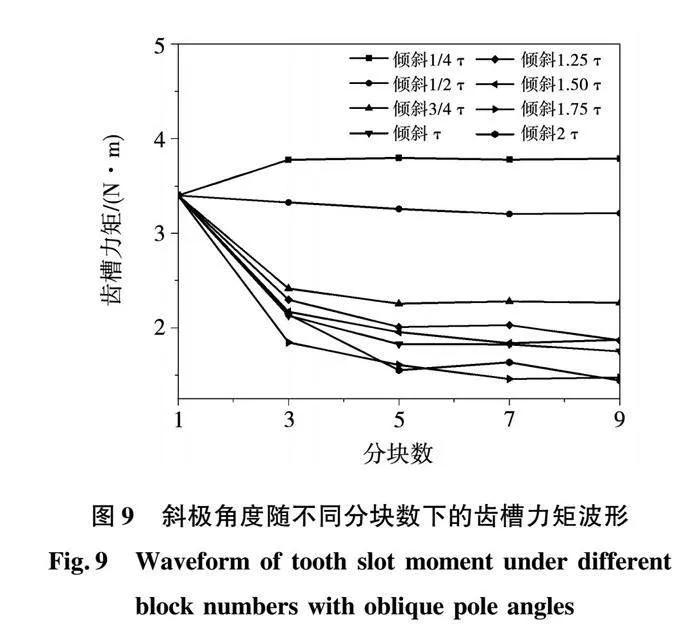
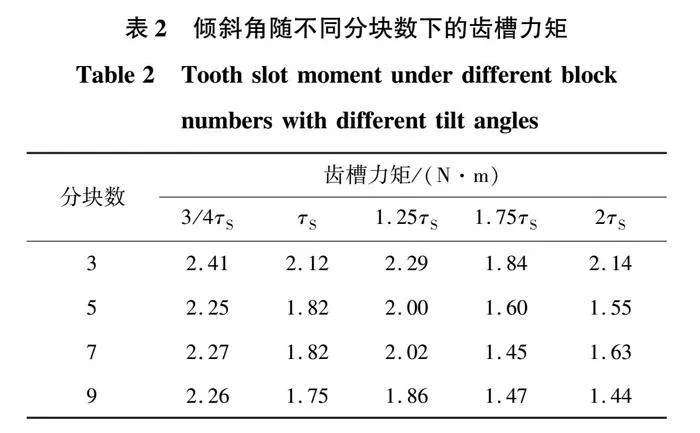
圖8（a）、（b）、（c）、（d）分別為不斜極、3、5、7段斜極電機模型。通過轉子斜極方法抑制電機的齒槽力矩首先要確定的就是斜極的角度，其中斜極角度與定子的槽距τS有關，如圖9的傾斜角度（不同槽距τS）隨不同分塊數下的齒槽力矩波形圖。

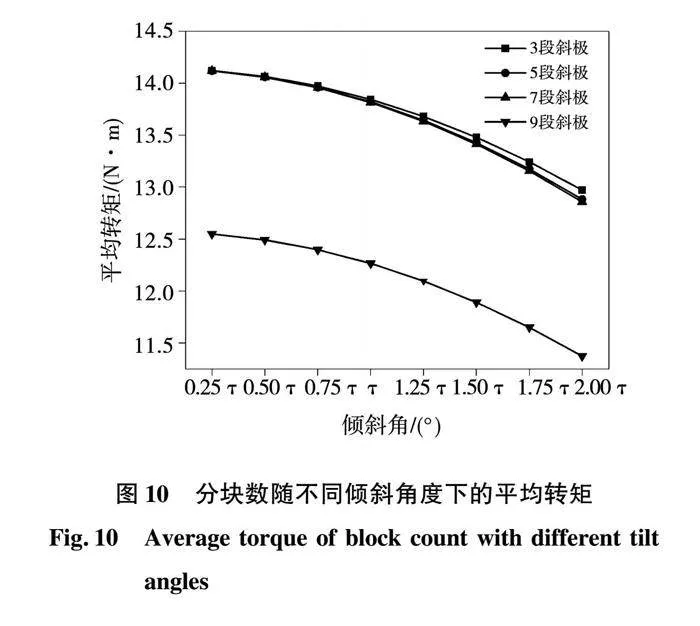
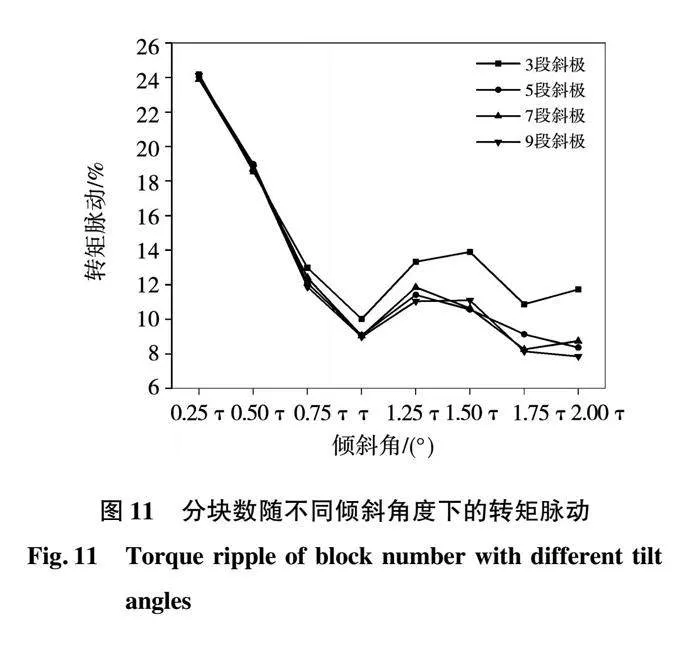
根據有限元仿真分析，當傾斜角度為1/4τS、1/2τS時隨著分段數的增加，電機的齒槽力矩并未有明顯變化，如下表2所示為傾斜角隨不同分塊數下的齒槽力矩，其中齒槽力矩下降最明顯的傾斜角度為2τS、1.75τS、τS，但隨著斜極角度的改變電機所能達到的平均轉矩也在變化，如圖10為分塊數隨不同傾斜角度下的平均轉矩，圖11為分塊數隨不同傾斜角度下的轉矩脈動。

隨著傾斜角度的增加不管在那種分段數下電機所能達到的平均轉矩都有所下降，其中采用9段轉子斜極時電機的所能達到的平均轉矩下降較為嚴重，不能夠達到電機所需要的額定電磁轉矩。其中采用3、5、7段轉子斜極時電機的平均轉矩下降趨勢較為相近，并且在采用τS～1.25τS傾斜角度時所能達到的平均轉矩與額定轉矩及其相近，從圖11可知當電機的傾斜角度為τS時電機的平均轉矩脈動最小其中分3段的轉矩脈動為9.56%；分5段時電機的轉矩脈動為9.08%；分7時電機的轉矩脈動為9.04%；分9時電機的轉矩脈動為8.98%。所以最終確定斜極的傾斜角度為τS，也就是1倍的定子槽距即為8.75°。

4.3 復合轉子結構對齒槽力矩的優化

前文已經單獨分析了不同方法下對齒槽力矩諧波的削弱，并且通過改變電機轉子結構對齒槽力矩優化的同時也要關注電機的其他性能，比如空載電勢、氣隙磁密等。通過結構優化方法分別分析了永磁體偏心距改變對電機轉矩特性的影響以及轉子斜極的方法對轉矩特性的影響。但單獨的方法含有局限性，所以將上述兩種結構優化方法合二為一，在調整電機轉矩特性的同時，本文還進一步提高電機的空載反電勢基波幅值和降低其諧波畸變率為優化目標。其中，空載反電勢諧波畸變率的具體表達式為。

（15）

式中：E1為空載反電勢基波幅值；Ej為空載反電勢第j次諧波幅值。

通過單獨的改變結構優化方法前文已經確定其變量的優化范圍，所以選擇中心復合表面設計，在求優的過程中，為了讓目標優化結果計算準確，采用式（16）的二階函數來擬合優化目標的數學模型。

（16）

式中：Y為系統響應；β為回歸系數；l為自變量個數；Ψ為擬合誤差；x為變量。

改變永磁體偏心距的方法對電機齒槽力矩的影響很大，追求齒槽力矩下降的同時還要關注電機其他的性能參數。這里為了保證減少計算量和結果的精度，截取偏心距優化區間為 [20，24]。由圖10可知，電機在采用3、5、7、9段斜極時轉矩脈動下降明顯，其中采用9段斜極下降效果最好，但此時電機的電磁轉矩低于額定值。所以在此優化過程中可以將分塊數的優化區間變為[1，7]。在此范圍內能夠滿足幾組優化變量的選取，也能減少不必要的計算量。優化變量的區間范圍為：

（17）

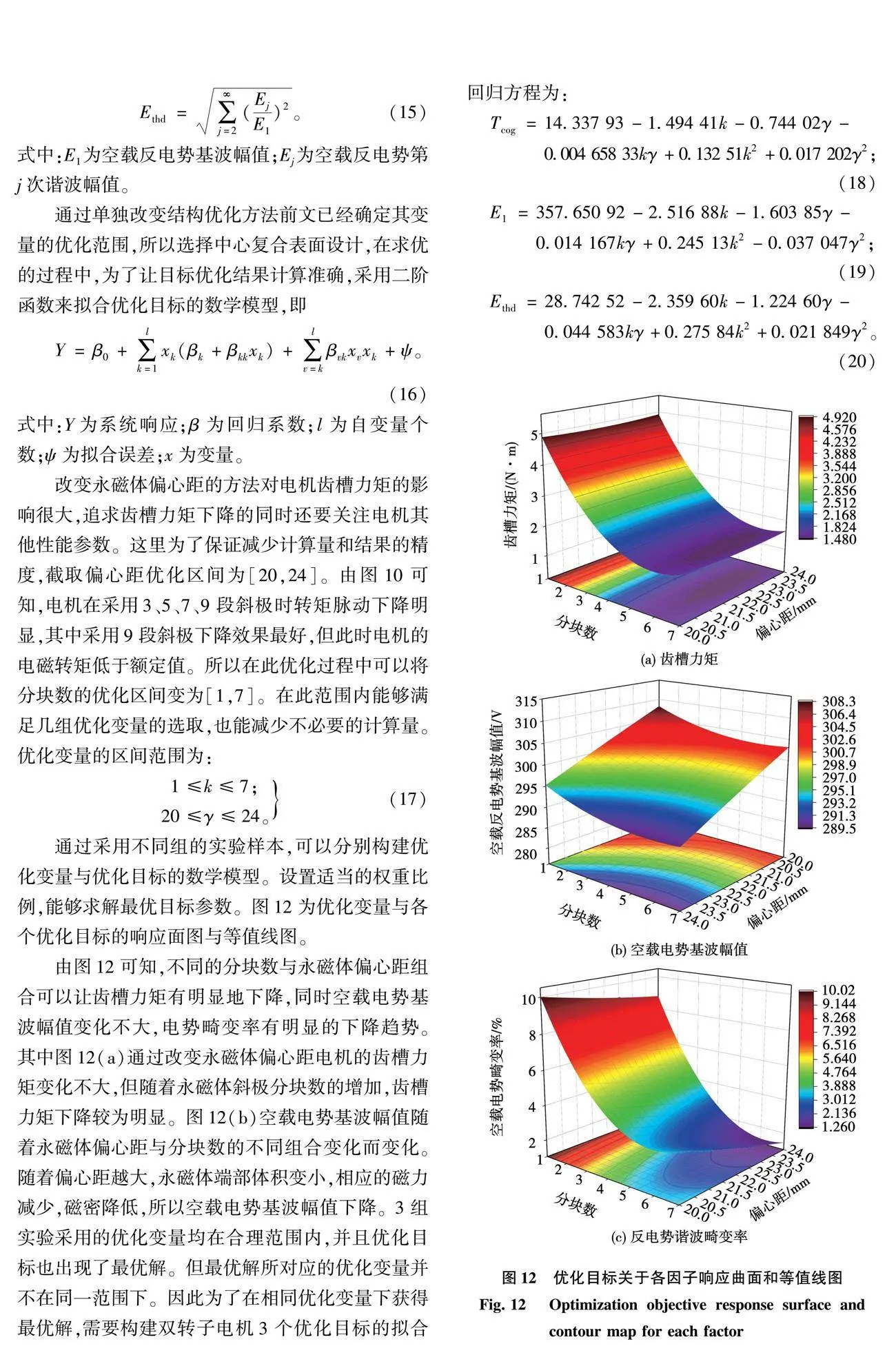
通過采用不同組的實驗樣本，可以分別構建優化變量與優化目標的數學模型。設置適當的權重比例，能夠求解最優目標參數。能圖12所示為優化變量與各個優化目標的響應面圖與等值線圖。

由圖12可知，不同的分塊數與永磁體偏心距組合可以讓齒槽力矩有明顯的下降，同時空載電勢基波幅值變化不大，電勢畸變率有明顯的下降趨勢。其中圖12（a）通過改變永磁體偏心距電機的齒槽力矩變化不大，但隨著永磁體斜極分塊數的增加，齒槽力矩下降較為明顯。圖12（b）空載電勢基波幅值隨著永磁體偏心距與分塊數的不同組合變化而變化。隨著偏心距越大，永磁體端部體積變小，相應的磁力減少，磁密降低，所以空載電勢基波幅值下降。3組實驗所采用的優化變量均在合理的范圍內，并且優化目標也出現了最優解。但最優解所對應的優化變量并不在同意范圍下。因此為了在相同優化變量下獲得最優解，需要構建雙轉子電機3個優化目標的擬合回歸方程為

（18）

（19）

（20）

本文研究的并軸雙轉子永磁電機含有較大的齒槽力矩和轉矩脈動，過大的轉矩脈動對電機的穩定運行有很大的影響，同時轉矩脈動還受到齒槽力矩的影響。所以需要在多目標優化電機的過程中，齒槽力矩變小，同時不影響電機的其他電磁性能。適當調整優化目標的權重比例可得出齒槽力矩、反電勢基波幅值和反電勢諧波畸變率預測值分別為0.89 N·m、205.17 V、3.27%。其中對應的優化變量斜極角度為8.75°，分塊數為5，偏心距為22.75 mm。

5 有限元仿真驗證

為了驗證上述優化方法的有效性，建立優化前后并軸雙轉子永磁電機的有限元模型，對其電磁性能進行對比分析。

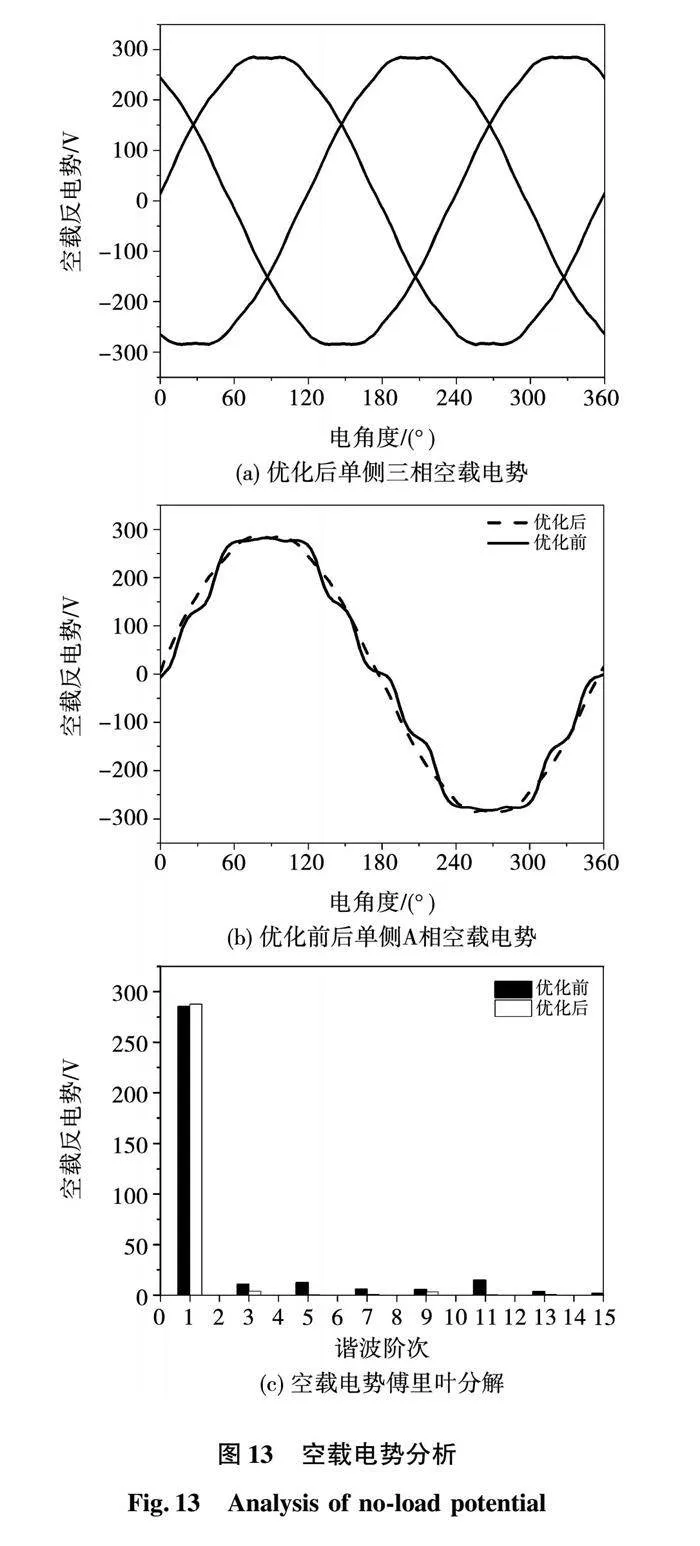
5.1 空載反電勢

優化前后電機的空載反電勢波形及其諧波含量如圖 13所示。圖13（a）為并軸雙轉子永磁電機優化后空載反電勢，能夠看出優化后的電勢波形為正弦波，并且三相電勢對稱，圖13（b）為A相優化前后電機的反電勢波形對比，優化前電機反電勢波形為平頂波并且具有較明顯的脈動。優化前后電機反電勢有效值分別為206.97、205.17 V；空載反電勢中總的諧波畸變率分別為8.5%和3.27%，其中空載電勢基波幅值增大，3 次和 5 次諧波優化后較優化前明顯下將，雖然在改變永磁體偏心距和斜極后電機的反電勢并沒有下降，仍然能夠保證電機的穩定運行。

5.2 齒槽力矩

優化前并軸雙轉子永磁電機由于定子含有邊端結構以及定子開槽的緣故，電機含有較大的齒槽力矩如圖14所示其幅值為5.9 N·m。優化后電機采用最優轉子斜極結構以及改變電機永磁體的偏心距可以將電機的齒槽力矩幅值控制在0.81N·m，其中齒槽力矩減小了86.27%。電機在不改變其他電磁性能的基礎上采用新的轉子結構，齒槽力矩有明顯的下降趨勢，轉矩脈動同樣得到抑制，電機能夠穩定運行。使得并軸雙轉子電機的齒槽力矩更加接近于傳統電機的齒槽轉矩，讓其滿足電機設計需求。

5.3 輸出轉矩

電機由于過大的齒槽力矩存在，在達到額定如圖15的電磁轉矩以外，電機的轉矩脈動過大。其中左右兩側輸出轉矩依次14.67、15.16 N·m，左右兩側轉矩脈動為24.61%、23.60%。優化后采用最優的轉子結構可以將電機的兩側轉矩脈動控制在9.94%、9.96%。能夠證明采用新型復合轉子結構對電機的齒槽力矩有很好的削弱效果，同時對電機的電磁性能起到優化的作用。

6 結 "論

本文以一臺并軸雙轉子永磁電機為研究對象，分析并軸雙轉子永磁電機齒槽力矩的特殊組成以及產生原理，主要由非削去部分固有的齒槽轉矩與邊端繞組槽所產生的邊端力共同組成。其中邊端繞組所產生的邊端力主要為2、4、6、8等偶數次諧波，并通過有限元分析驗證了理論分析的正確。提出一種復合轉子結構優化方法削弱電機齒槽力矩。采用曲面響應法建立了永磁體偏心距和分段斜極與多個優化目標的數學模型，并最終確定最優偏心距為22.75 mm、轉子斜極角度為8.75°、斜極分塊數為5段。采用最優的轉子結構，對比優化前后電機的電磁性能。其中，齒槽力矩在優化后由原來的5.9 N·m下降到0.81N·m。轉矩脈動由原來的左右兩側24.61%、23.60%下降到9.94%、9.96%。轉矩脈動得到明顯抑制。電機的空載電勢基波幅值增大，畸變率明顯下降。并軸雙轉子永磁電機電磁性能得到進一步改善。

參 考 文 獻：

[1] HWANG C C， JOHN S B， WU S S. Reduction of cogging torque in spindle motorsfor CD-ROMdrive [J]. IEEE Transactionson Magnetics， 1998， 34（2）：468.

[2] ZHU Z Q， HOWE D. Influence of design parameters on cogging torque in permanent magnet machines [J]. IEEE Transactions on Energy Conversion， 2000， 15（4）：407.

[3] YANG Yubo， WANG Xiuhe， ZHANG Rong， et al. Research of cogging torque reduction by different slot width pairing permanent magnet motors[C]// International Conference on Electrical Machines and Systems （ICEMS 2005）， September 26-29， 2005， Nanjing， China. 2005：367-370.

[4] HANSELMAN D C. Effect of skew， pole count and slot count on brushless motor radial force， cogging torque and back EMF [J]. IEE Proceedings - Electric Power Applications， 1997， 144（5）： 325.

[5] LUKANISZYN M， JAGIELA M， WROBEL R. Optimization of permanent magnet shape for minimum cogging torque using a genetic algorithm [J]. IEEE Transactions on Magnetics， 2004， 40（2）： 1228.

[6] LI Y， XING J， WANG T， et al. Programmable design of magnet shape for permanent-magnet synchronous motors with sinusoidal back EMF waveforms [J]. IEEE Transactions on Magnetics， 2008， 44（9）：2163.

[7] LI Yong， ZOU Jibin， LU Yongping. Optimum design of magnet shape in permanent-magnet synchronous motors [J]. IEEE Transactions on Magnetics， 2003， 39（6）：3523.

[8] ZHU L， JIANG S Z， ZHU Z Q， et al. Analytical methods for minimizing coggingtorque in permanent magnet machines [J]. IEEE Transactions on Magnetics， 2009， 45（4）： 2023.

[9] CHANG Jiujian， MA Wenli， HUANG Jinlong. Design and optimization of arc permanent magnet synchronous motor used on large telescope [J]. IEEE Transactions on Magnetics， 2012， 48（5）： 1943.

[10] HU Hengzai， ZHAO Jing， LIU Xiangdong， et al. Research on the torque ripple and scanning range of an arc-structure PMSM used for scanning system [J]. IEEE Transactions on Magnetics， 2014， 50（11）：1.

[11] ZHU Y W， KOO D H， CHO Y H. Detent force minimization of permanent magnet linear synchronous motor by means of two different methods [J]. IEEE Transactions on Magnetics， 2008， 44（11）： 4345.

[12] ZHU Y W， LEE S G， CHUNG K S， et al. Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM [J]. IEEE Transactions on Magnetics， 2009， 45（6）： 2863.

[13] INOUE M， SATO K. An approach to a suitable stator length for minimizing the detent force of permanent magnet linear synchronous motors [J]. IEEE Transactions on Magnetics， 2000， 36（4）： 1890.

[14] CHUNG S U， KIM J M. Double-sided iron-core PMLSM mover teeth arrangement design for reduction of detent force and speed ripple [J]. IEEE Transactions on Industrial Electronics， 2016， 63 （5）： 3000.

[15] CHUNG S U， LEE H J， WOO B C， et al. A feasibility study on a new doubly salient permanent magnet linear synchronous machine [J]. IEEE Transactions on Magnetics， 2010， 46（6）： 1572.

[16] 戴思銳. 雙螺桿用并行直驅連體永磁電機研究[D].沈陽：沈陽工業大學，2022.

[17] 陶大軍，陳陽，李凌霄，等.MW級雙并列轉子低速永磁直驅電機設計方法與性能分析[J].電機與控制學報，2023，27（9）：82.

TAO Dajun， CHEN Yang， LI Lingxiao，et al. Design method and performance analysis of MW-level dual-parallel rotor low-speed permanent magnet direct-driven motor[J]. Electric Machines and Control，2023，27（9）：82.

[18] ZHU Z Q， RUANGSINCHAIWANICH S， HOWE D. Synthesis of cogging-torque waveform from analysis of a single stator slot [J]. IEEE Transactions on Industry Applications， 2006， 42（3）： 650.

[19] BIANCHINI C， IMMOVILLI F， BELLINIA， et al. Arc linear motors for direct drive robots： Galileo sphere[C]//2008 IEEE Industry Applications Society Annual Meeting， October 5-9，2008，Edmonton， AB， Canada. 2008：1-7.

[20] ZHU L， JIANG S Z， ZHU Z Q， et al. Analytical methods for minimizing cogging torque in permanent magnet machines [J]. IEEE Transactions on Magnetics， 2009， 45（4）： 2023.

[21] "胡鵬飛，王東，靳栓寶，等．偏心磁極永磁電機氣隙磁場正弦優化模型[J]. 電工技術學報， 2019，34（18）：3759.

HU Pengfei， WANG Dong， JIN Quanbao， et al. Sinusoidal optimization model for air gap magnetic field of eccentric magnetic pole permanent magnet motor[J]. Transactions of China Electrotechnical Society，2019，34（18）：3759.

[22] "呂東元，呂奇超，李延寶，等.磁懸浮儲能飛輪高速永磁電機設計及優化[J].大電機技術，2022（2）：6.

LV Dongyuan， LV Qichao， LI Yanbao，et al. The design and optimization of high-speed permanent magnet machines for maglev flywheel energy storage system[J]. Large Electric Machine and Hydraulic Turbine，2022（2）：6.

[23] "溫嘉斌，于嵐.田口方法在永磁同步電機結構優化中的應用[J].哈爾濱理工大學學報，2019，24（5）：64.

WEN Jiabin， YU Lan. Application of taguchi method in structure optimization of permanent magnet synchronous motor[J]. Journal of Harbin University of Science and Technology， 2019，24（5）：64.